КОНСПЕКТ ЛЕКЦИЙ

по физике

Часть 1

Механика, колебания, волны

1

Математическое введение

ax + bx + c = 0 ; x_1,2 =

1.2. Длина окружности: .

Площадь круга: S = 4ππ = πd² .

4

Объем шара:

Длина дуги окружности: l = j × R

2

Площадь сектора:

Угол j выражается в радианах.

1.3. Приращение величины x:

: т.е. разность между конечным и начальным значением

_{х. Убыль величины x :} - ∆x = x - x

1.4. a₁ + a₂ + .....a_i + ......a_n = , где знак

i=1

есть сумма значений величин по I от 1 до n

1.5. - отношение противолежащего катета к

гипотенузе;

cosa = - отношение прилежащего катета к гипотенузе;

- отношение прилежащего к противолежащему катету;

ctga = ,

sin(-a ) = -sina ;cos(-a ) = cosa

2

tg(-α) = -tgα ; ctg(-α) = -ctgα

sin0⁰ = 0;sin90⁰ = 1;sin180⁰ = 0;

cos0⁰ = 1;cos90⁰ = 1;cos180⁰ = -1

1.6 cos(90⁰-a) = sina ; cos(90⁰+a) = -sina

cos(180⁰-a) = -cosa ; cos(180⁰+a) = -cosa

cos(270⁰-a) = -sina ; cos(270⁰+a) = sina

cos(360⁰-a) = cosa ; cos(360⁰+a) = -cosa

1.7. Векторы – величины, характеризующиеся численным значением, направ-

лением и складывающиеся по правилу параллелограмма (треугольника,

многоугольника). Модуль вектора - численное значение вектора: a = a

_r

1.8. Сложение векторов: с = а + b ; _{c = (a + b}² _{+ 2abcosa)}^{1 2}

_r

Вычитание векторов: c = a - b

r

_b a a

1.10. a = ae_a - единичный вектор или орт вектора , который по

_r

направлению совпадает с вектором .

e_a ↑↑ а e_a = 1

^{1.11. ◉ - вектор}

3

пендикулярно плоскости рисунка и к “нам”

Ä - вектор направлен перпендикулярно плоскости рисунка и от

“нас”.

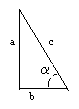
1.12. Разложение вектора на составляющие:

a = a + a .

В общем случае:

a = a + a + a_z ,

где a_x , a , a_z - составляю-

щие вектора a вдоль коорди-

нат x, y, z. Составляющие вектора являются векторами.

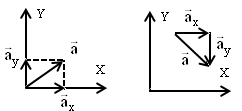
1.13. Проекции вектора: a = acosα ; a = acosβ ;

a - проекции вектора на координатные оси x, y; a и b - углы

между вектором a и положительными полуосями a = a e_x + a e_y ;

a = (a + a )^{1 2}

В общем случае:

a = a e_x + a e_y + a e_z

a = (a² + a² + a²)^{1/ 2}

где e_x , e_y , e_z - единичные векторы

(орты) координаты осей x, y, z ;

e_x = e_y = e_z = 1

x

1.14. Скалярное произведение двух

r

r

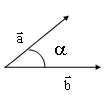
b

b_a - проекции вектора b на вектор a .

_{r r}

а b = b a - скалярное произведение двух векторов

коммутативно, т. е. не зависит от порядка располо-

жения сомножителей.

a = aa = aa cos 0 = a

4

1.15. Векторное произведение двух векторов:

r r r

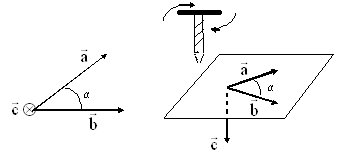
Вектор перпендикулярен плоскости, в которой лежат векторы a и b .

Направление вектора (векторного произведения) определяют по пра-

вилу правого винта (буравчика): буравчик располагают перпендикулярно

плоскости, в которой лежат векторы a b и вращают от первого сомно-

жителя (вектор a ) ко второму (вектор b ) по кратчайшему пути. Поступа-

тельное движение буравчика совпадает с направлением вектора .

Производная.

y = f (x) ; ∆x и ∆y приращение аргумента x и функции y.

Dx ® 0 обозначают dx – бесконечно малое приращение аргумента, Dy ®

0 обозначают dy - бесконечно малое приращение функции.

∆y

равно тангенсу угла наклона секущей.

∆x

5

Производная от y: = (= y')

При Dx ® 0 и Dy ® 0 секущая переходит в касательную. Следовательно:

графически производная равна тангенсу угла наклона касательной:

dy/dx = tgα

Для дальнейшего отметим, что в физике производные не принято

обозначать значком «штрих: у’». Есть специальные обозначения

только для функции времени. Если z = f (t) , то производная по времени

обозначается следующим образом: z = (= z').

2

Вторая производная: .

1.17. Производные: постоянной, произведения постоянной на функцию,

суммы (разности), произведения, частного.

А. Производная от постоянной величины равна 0, т.е. если y = c, где

с = const , то y’=0

Б. Постоянный множитель можно вынести за знак производной, т.е. если

y = cu (x), где c = const, то y’=c×u’(x).

В. Производная от суммы (разности) функций равна соответствующей

сумме (разности) производных этих функций, т.е. если

y = u(x)+ v(x)+ w(x) , то” y = u (x) + v (x) + w (x).

Г. Если y = u(x)×v(x) , то” y = u (x)×v(x) + u(x)×v (x)

u(x) u (x) × v(x) - u(x) × v (x)

v(x)

1.18. Некоторые табличные производные:

(xⁿ ) = nx^n-1 , (e^x ) = e^x , (a ) = a ln a

, (cos x) = -sinx , (sinx) = cosx

, (ctgx) = -

Если a = const , то (cosax) = -asinax , (sinax) = acosax.

6

1.19. Частная производная. Если z есть функция двух переменных x и y,

то частной производной по x от функции z = f (x, y) называется произ-

водная по x , вычисленная в предположении, что y есть постоянная вели-

чина. Аналогично определяется частная производная по y.

z = x y³ , то” = 2xy³ , = 3x²y²

1.20. Дифференциал функции.

Если , где dy - дифференциал функции

y = f (x) – т.е. бесконечно малое приращение функции при бесконечно

малом приращение аргумента.

S » Dx_i - площадь ограниче-

ния кривой y(x) на участке от a до b.

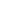
S = Dx_i ⇒

Dx_i ®0

это есть интеграл

Первообразная F(x) для функции

y(x):

b

y(x)dx = F(x) = F(b) - F(a)

b

= ln x = ln b - ln a = ln

1.22. Интеграл от суммы (разности) функции равен сумме (разности) ин-

тегралов, т.е.

∫^{[f (x) + f2 (x) - f3(x)]× dx =} ∫^{f (x)dx +} ∫^{f (x)dx -} ∫^{f (x)dx}

Постоянный множитель можно выносить за знак интеграла, т.е.

c × f (x)dx = c_∫ f (x)dx , где с - постоянная величина.

Некоторые табличные интегралы.

∫^{dx = x + const ;} ∫

7

n+1

x dx = + const; где n ¹-1;

n + 1

∫^{e dx = ex + const}

∫^{cos x × dx = sin x + const ;} ∫^{sin x × dx = - cos x + const}

8