§ 24. Принцип относительности Галилея

Рассмотрим две системы отсчета (рис. 24.1). Систему обозначен-

ную K, будем считать неподвиж-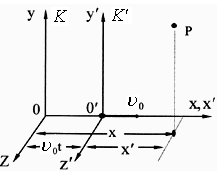

ной, систему K¢ - подвижной; ее

скорость относительно неподвиж-

ной системы постоянна и равна u₀ .

Координатные оси систем выберем

так, что бы они были параллельны

друг другу; в начальный момент

времени начало координат систем

совпадает; скорость u₀ направлена

вдоль оси х. (Такое расположение

осей выбрано для упрощения вида

Рис.24.1 _{нижеприведенных уравнений. Вы-}

воды, которые будут получены,

справедливы для любого взаимного расположения систем K и K¢).

Найдем связь координат некоторой точки «р» в системе K с ее

координатами в системе K¢ . Из рис. (24.1) видно

x=x¢+u₀t; y=y¢; z=z¢; t=t¢ (24.1)

(Последнее из равенств (24.1) означает, что длительность некоторого со-

бытия в системе K и K¢ - одинаковое). Уравнения (24.1) называются пре-

образованиями Галилея.

Найдем связь между скоростями точки “р” по отношению к си-

стеме отсчета K и K¢ :

u_x = x; u_x = x ⇒

Из (24.1) следует: x = x +u₀ ⇒ u_x = u_x + v₀ ,

u_y = u_y ; u_z = u_z ⇒

u = u +u₀

где u - скорость точки относительно системы K, u -скорость точки от-

носительно системы K¢ ,u₀ -скорость подвижной системы относительно

69

неподвижной системы. Соотношение (24.2) дает правило сложения скоро-

стей в классической механике.

Найдем ускорение в системе K и K¢ :

a = u; a = u

После дифференцирования (24.2) получим (учитывая, что

r r

(24.3)

Отсюда следует, что ускорение тела во всех системах отсчета, движущих-

ся друг относительно друга прямолинейно и равномерно, одинаковое. В

частности, если одна из систем инерциальная (т.е. при отсутствии сил

a = 0 ), то и остальные будут инерциальными (т.е. a = 0 ).

Второй закон Ньютона в системе k и k‘будет иметь вид:

F = ma; F = ma (24.4)

Из (24.3) и (24.4) следует, что силы, действующие на тело в системе k и

k‘тоже одинаковые. Следовательно, уравнения динамики не изменяются

при переходе от одной инерциальной системы отсчета к другой, т.е.

уравнения динамики инварианты по отношению к преобразованиям коор-

динат от одной инерциальной системы отсчета к другой. С механической

точки зрения все инерциальные системы отсчета эквивалентны: все ме-

ханические явления в различных инерциальных системах отсчета проте-

кают одинаковым образом. Это утверждение носит название принцип от-

носительности Галилея.

§ 25. Постулаты Эйнштейна.

Преобразования Лоренца, следствия из них

Специальная теория относительности Эйнштейна (релятивистская

механика) основана на двух постулатах (утверждениях), которые носят

названия принцип относительности Эйнштейна и принцип постоянства

скорости света

Принцип относительности Эйнштейна является распространени-

ем принципа относительности Галилея (механического принцип относи-

тельности) на все физические явления. Согласно этому принципу все за-

коны природы одинаковы во всех инерциальных системах отсчета. Сле-

довательно, уравнения, выражающие законы природы, инварианты по

отношению к преобразованиям координат и времени от одной инерциаль-

ной системы отсчета к другой.

70

Принцип постоянства скорости света утверждает, что скорость

света в пустоте одинакова во всех инерциальных системах отсчета и не

зависит от движения источников и приёмников света

Возьмём две инерциальных системы отсчета, аналогичных тем,

что рассмотрены в § 25: система K неподвижная, система K¢ движется

относительно системы K со скоростью u₀ . Для того чтобы выполнялись

постулаты Эйнштейна переход от координат и времени, отсчитанных в

системе K¢ , к координатам и времени, отсчитанных в системе K , должен

выполнятся согласно следующим соотношениям:

x +u₀t t + x u₀ c²

2 2

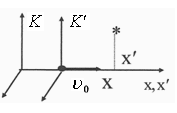
лённый промежуток времени. Свяжем с

этой точкой систему отсчета K¢- точка

относительно системы K¢ покоится, си-

стема K¢движется относительно системы

K со скоростью u₀ (рис. 25.1). Началу

события в системе K¢ соответствует неко-

торый момент времени t¢₁, концу события

– t¢₂, событие происходит в одной и той же точке с координатой x¢. Дли-

тельность события в этой системе координат равно ¢ - t₁

∆t₀ - это время, измеренное по часам, движущимся со скоростью тела, в

котором происходит событие. Это время называют собственным време-

нем тела.

Найдем длительность этого события в системе K¢. В этом случае

длительность события определяется по неподвижным часам. Началу со-

71

бытия в этой системе отсчёта соответствует момент времени t₁, концу

события – t₂. Время t₁и t₂ согласно преобразованиям Лоренца (25.1) рав-

ны:

t₁ = t₂ = (25.2)

Длительность события в системе K:

∆t=t₁-t₂ (25.3)

Подставим в (25.3) уравнения (25.2):

∆t = t₂ - t₁ = ⇒

2

(25.4)

2

Интервал времени Dt - это длительность события измеренная по непо-

движным часам, Dt₀ - длительность события измеренная по часам дви-

жущимся со скоростью u₀ . Из уравнения (25.4) следует, что Dt > Dt₀ ,

поэтому можно сказать, что движущееся часы идут медленнее, чем поко-

ящиеся, а собственное время наименьшее.

II. Длина тел в разных системах. Пусть имеется стержень, расположен-

ный вдоль оси x и двигающийся со скоростью u₀. Аналогично пункту I

можно показать, что длина стержня l₀ в системе K¢ (т.е. длина покояще-

гося стержня) и длина стержня l в системе K (т.е. длина, измеренная в

системе относительно которой он движется) разная. Повторяя рассужде-

ния пункта I, получим:

1 -u₀ c²

Видно, что l < l₀ , т.е. у движущихся тел размеры их в направлении дви-

жения сокращаются тем больше, чем больше скорость движения. Это яв-

ление называется лоренцевым сокращением.

III. Сложение скоростей. Для упрощения формул будем считать, что

скорость частицы параллельна оси х. Тогда модуль скорости частицы в

системе K и K¢ соответственно равен:

¢

υ = υ_x = ; υ' = υ'_x =

dt dt

¢ ¢ ¢ ¢

dx = ⇒ dx = dt ⇒

1-u₀ с² 1-u₀ с²

dx = dt , (25.6)

2

dt + dx u₀ /c² ¢ ¢

1-u₀ с² 1-u₀ с²

dt = dt . (25.7)

2

Разделим уравнение (25.6) на (25.7) и учтём (25.5):

u'+u₀

. (25.8)

1+u'u₀ с²

В случае малых скоростей u₀ << c формула (25.8) переходит в формулу

сложения скоростей классической (нерелятивистской) механики

(§ 24,ур-е (24.2)).

Пусть скорость u'= c . Из (25.8) получим:

u = = c

1+ cu₀ с²

что согласуется со вторым постулатом Эйнштейна.