2.2. Методы формализованного представления систем1

Классификации МФПС. Математика непрерывно развив” ^. Возникают новые области и математические теории, отмиракп ^^ вливаются в другие устаревающие разделы. Исследование” зя^Уктуры (или, как принято говорить архитектуры) математик” •у симаются многие ученые (см., например, [2.2, 2.14, 2.41, 2.26, 2.45,

-^идр.]).

Несмотря на то, что в практике моделирования широко ис. 'ьзуются теория множеств, математическая логика, математиче. ч лингвистика и другие направления современной математики, tux пор еще не все ученые-математики склонны включать в чис. ^ математических некоторые из этих направлений. Благодаря ра. и •ам французских ученых (публикующихся под псевдонимом чурбаки [2.6]), теорию множеств и математическую логику стащ

-Узнавать разделами математики, а математическую лингвистик) ^-^миотику часто еще не относят к математике. Поэтому, чтобы не „^уждать различные точки зрения (которые постепенно изменяют-

-развиваются), вместо термина "математические методы" удобна ^р^менять предложенный в [2.11] термин "методы формализованно представления систем".

фик ® большинстве первоначально применявшихся при исследовании систем класси-ндц^ций выделяли детерминированные и вероятностные (статистические) метода

классы моделей, которые сформировались в конце прошлого столетия. лис” Ччтем появились классификации, в которых в самостоятельные классы выдели-нек'* теоретико-множественные представления, графы, математическая логика“ го ц-торые новые разделы математики. Например, в классификации современно ^^математического аппарата инженера В.П.Сигорский [7] выделяются: множеств

4>ицы, графы, логика, вероятности.

ньге В одной из первых классификаций, предложенных специально для целей систем е^ исследований украинским академиком А.И.Кухтенко [2.28], наряду с выделен” pl.^vav.m уровней ма-гематического абстрагирования, как общеалгебраический, тес-фортка-множественный, логико-лингвистический, предлагается рассматривать “” ^анионный и эвристический уровни изучения сложных систем.

Имеются н другие классификации (см., например, [2.47]).

В данном учебнике принята и кратко характеризуется классифи-

•^ия Ф.Е.Темникова, предложенная в [2.11], в которой выделяюто >чующие обобщенные группы (классы) методов (табл. 2.1): она-

•гические (методы классической математики, включая интегро

•Ьференциальное исчисление, методы поиска экстремумов функ-1, вариационное исчисление и т. п.; методы математического •\>граммирования; первые работы по теории игр и т. п.); стати-

^ческие (включающее и теоретические разделы математики -

т оию вероятностей, математическую статистику, и направления и якладной математики, использующие стохастические представ-Jit ния - теорию массового обслуживания, методы статистических Испытаний (основанные на методе Монте-Карло), методы выдви­жения и проверки статистических гипотез А.Вальда и другие ме-т-оды статистического имитационного-моделирования); теоретико-множественные, логические, лингвистические, семиотические пред­ставления (методы дискретной математики), составляющие теоре-т-ическую основу разработки языков моделирования, автоматиза­ции проектирования, информационно-поисковых языков; графиче­ские (включающие теорию графов и разного рода графические представления информации типа диаграмм, гистограмм и других

графиков).

Разумеется, в табл. 2.1 приведены лишь укрупненные группы-Направления, конкретные методы которых только в начальный период развития характеризуются рассмотренными особенностями. Эти направления непрерывно развиваются, и в их рамках появляют­ся методы с расширенными возможностями по сравнению с исход­ными.

Кроме того, в математике постоянно возникают новые направ­ления как бы "на пересечении" методов, отнесенных к приведен­ным укрупненным группам. В частности, на пересечении аналити­ческих и теоретико-множественных представлений возникла и раз­вивается алгебра групп; параллельно в рамках алгебры групп и теории множеств начала развиваться комбинаторика', теоретико-множественные и графические представления стали основой воз­никновения топологии; статистические и теоретико-множественные методы инициировали возникновение теории "размытых" множеств Л.Заде [3.7], которая, в свою очередь, явилась началом развития нового направления - нечетких формализации и т. д.

Отметим, что понятия исходных направлений не всегда сохраняются в неизмен­ном виде; в частности, в теории Заде дается иная трактовка понятия вероятности по сравнению со статистической.

Практически невозможно создать единую классификацию, ко­торая включала бы все разделы современной математики. В то же время -приведенные направления помогают понять особенности конкретных методов, использующие средства того или иного на­правления или их сочетания, помогают выбирать методы для кон­кретных приложений.

^i “с з х а- и- а - s е- ь” 'С 2 ^ 1 S t-u § " s 0 2 ft 0 ев X eg 0. CJ •fr U	|ill|:ptH£l|£i ilh ^III ^1 Illlllpi^i^ Illii iliJEll 1 M !ii!ji liE lil i ISii'Hfii III} iiSSI siiii'i^^^phjiMi w w ^wwwim i5 ihii li • iiSil ig5^-в'=£g-гs£:taFЗas^з2xSF§,s '"9"^ й-|5ьйSsc§й|5м^5==ss"£' ^.^.о ^^^.-"“Узо^^^^^ё.^з^^з?!^ ^йр u^sss^a.ug^^^glgl^^g^i^z^g ^^Ess^^ss^ss-sss^^iiisge"- hss s-se-et^e-s^ 5.£g^?s^ieS?g-§ ь^яё и4и1-чп2э-с(3=2сэв2= ySF'Ssrasg? '• •' .———————————————————————————————————————————————————————————
is SSg -” сч О c.=£ 0 y 5SZ 5.23 "Зй = ° 5 K S jis" iis £ 2 s=£- 0. t- HW S *' к 3" ll§ 5 '" §? “> x “ y§s я 5 o. ss'g t, " Ч S--S SS5 5 9 д?	§2?.i^|U-5Ss^ g?^- s^g-is Ul! eil-g^5 .Bs-l^sl^iil^lilll ii r.^lH^s Is ^si •;^i|l ^j^ Ш^^- s|^I||^|:-|g<.|..igl| |, a.= eeo,..Q•^ozзl-Sзi sra3^ =ь 5. '•'я о. cS”-°o= ^”l-t1яo502co*'тг„г(D их" ь ^5&2££|?0"^S S !з5|§. SeSe^S -5-5 ”|.2-^g.?S 5?S^S c 5.-§-£.-ё а 8 „ 5-^ £2 ^1^:1 ^^i^ is а' shi^ h:s il-lseih.^i^Hiiip^i :^ i. illl^ll:!^: Illl Bjil^ li^i^ll:^2!^^!^!^^^! |H 11 III 11 ^ i^ bi-uux— я— -rtuincia: i-uo.g во.5“<“ ——————————————————————————^————————————————————————————————
	£ ч “о ^ u^^^ 5| ^T°

—•* г” 1 ^ s &i S -3 a .5.	i сч	Ipl 1НЩ?||Щ€Ц1||.1|8 s^ifs ||^|l|J^I;tg И&1 mi tiliili iSli !ill 1Ш it. ifii i.lir| ^^p-slisl^i^^ipb ,е^!г- ll-ieB?^:"!;? lijs 5-i:2 Н:Ш -ii^^i^l^ JJI.bis Л ^И^Ь §1^ !li . EiliSiil tl|i •li 11 SSe^S S S 3 3 S “I 5 x a? S c? xSS-e-Poii g2^xat)x3 u^a то т cf aiCQ u о ае ^ u ”;“•=(
	CM	a 5g'=”.2°->'S S'S=°~° "S^S Й23"С>>> '0?S g^rtie^ es.5'^^-'У So "So^o^g. 2 Si SSo^o.gg.x 6 tj^5^| 5:S^5 .se^l^Sg^ ё2! §?§5|ё l^-slll5^! ^iS:^'S ^^йз^од-^ ^1;=^^1 sl--'s P:^!!^- 30^ ^^^ 5?-|§'lgS^ ^s.xl^5 гП^53 ^1 Bffi in ii® Hi ill -ig.SC^gSQ. ss'p'-'s ""^^^^(^''"-вг <o”o" Cni-ueS" "o-s -э-в^йс^За с:- ^"•cS0-0!^"'^^”?' sil^'slis?^'"'^ ^i^lTyss ^> =-:°?|g ^Is^g.gs-lsilj:!^!.^'!5^^ iill.l !13 i!i Ilif i lilllgii'J^ill^Jsling-le^l iIJ^^j^&lis'x^-^ltlll-TlllP^^^^ SsS^S'SraSn'^o.Ocao.-.-ist-catibg.^Seto а” SSfiaeiZoon.'^aSSSSl^SuOO.o'g'iSsgogo.oy И Д -S-S S?a;a£o. ccbxo";* eonfftt.ai'^uoi. 'ic ”2вх>.г;х с<>;сожо?-3и гаоь.Е.жсц £^,”iu0.s3cs6
	—	• ^-' Д 11 „^ j | f>^ 11/Xr^ in^^ OJ 3 t 1 C10^' ^ *^—' &S \J^-—^ . “2 B-i2 s

•^ <-i 1 ^ £ i-	0	ш • и	^-^sss ^His.s^p:!-^ i^alsj fs. t i^l^ g^siglii^ii l^J 1 := &sj5?sg'3 gl^-^-^agEe-!^61 ££"5"^ Ss iiiltli ч ^i^ss-^^^gsss-^lss.^b^ae-^ ss—egi s? s^lESS-s^sgg.-o.igsg ^ -” sg^g-s1! *.5 g"" ts'OaSta0- "xS^^0"!;3'1-- uo3"5xp 5 Ы 8§|:5 |^5|2J|S|J;| i3||.|5 ISI llllilllt^Ciliillililll^^lii^ii §?^.55£?S.K c=F 5 5 S as =• 8 ik ч S b! ” 2 >,==са:ч— =• о.
		'§.3§- Sx=S.i<2"§?'2 .^““ui-^sci. “S ^s^ "s^^s^c s.Ss5°|ss.§. ss |^“ sss^^^l^ "sss^s^e^ s'§ |^5| jS.l^ggeS^ ч”'^^”'^ !5 lis .1:^:1^1 iis^§ji :s 1^ PI Si. 11 "•SsS ||^2."sSs-s as^sig.gg31 i| ggo. 5^"g£H^^ SSLgle-^gS S" ge-ts iei^^i^^ x^^sas^s h '^s.^l^s;?! "li^llss.s 1| ir.5|i!ijirJjl ih53^^:-! Ill^^fllii^l ppl;; ills: ^^3 l^lii2? lil:|liliir-dllrllliillil ^!|ltl!|g"|
	сч	PI H|:| 1111 |1 lil.lSIII Ш Й lil !l|lt !l| ^: Щ^ |l^ilslPilli|s|l 1 IBi^-iriiljil^ls'lil §|Ц§!^§1 .p 5|. hsls.Psses^^gin^ "З!^"^:^^^^^^^^? it^ttg^li ^Ig-g.s^gjsl^^^l^li^^^g^asl^i'i.a^fe ^^^"^^'^-^“gIg-lsa.y^l^g.aSgitlSaiS-s-
	-	1"“ / “)>. ^ lilrrr^--I^U---^ 2 о С ь-; с:; 5 5 о. <U 0. О ч 13	^ i! ^J^^T я с J^ £•5 &• u

Прикладные классификации МФПС. Для удобства выбора ме­тодов решения реальных практических задач на базе математиче­ских направлений развиваются прикладные и предлагаются их клас­сификации.

Так, существуют различные классификации экономико-матема­тических методов, обобщение которых приведено в табл. 2.2. Эта классификация включает прикладные направления, базирующиеся, в основном, на использовании аналитических и статистических представлений. Однако некоторые из них (модели объемного и ка­лендарного планирования, потоковые модели) используют графи­ческие методы (сетевое моделирование), а иногда для предвари­тельного описания задачи - теоретико-множественные представле­ния.

Когда начали широко развиваться автоматизированные систе­мы сбора, хранения и поиска информации, разного рода, появилась потребность в разработке классификаций методов работы с инфор­мационными массивами. Одна из таких классификаций, предложен­ная в [2.1], приведена в нижней части табл. 2.2. Эти классификации, напротив, базируются на использовании методов дискретной мате­матики, и в основном графических и теоретико-множественных представлений с элементами математической логики.

Классификации, ориентированные на прикладные направления, можно сопоставить с классификациями математических методов, что сделано в табл. 2.2. Получаемая двумерная классификация удобна тем, что в нее можно "входить" через прикладные направле­ния ("слева") и через математические ("сверху"), что помогает при организации взаимодействия проектировщиков и управленческих работников, использующих прикладные классификации, со специа­листами-математиками, которые помогут пояснить принципиаль­ные теоретические возможности выбираемых математических мето­дов.

При выборе метода моделирования для постановки принципи­ально новых задач с большой начальной неопределенностью удоб­но связать классификацию методов формализованного представле-. ния с классификацией систем. В частности, приведенную в таблице классификацию методов формализованного представления сис­тем можно связать с классификацией систем по степени организо­ванности: если предварительный анализ проблемной ситуации по­казывает, что она может быть представлена в виде хорошо орга­низованных систем, то можно выбирать методы моделирования из классов аналитических и графических методов; если специалисты по теории систем и системному анализу рекомендуют представить ситуацию в виде плохо организованных или диффузных систем, то следует обратиться прежде всего к статистическому моделирова­нию, а если не удастся доказать адекватность ее применения, то

90

искать закономерности в специальных методах (например, в эконо­мике, социологии и т. п.); при представления ситуации классом са-^оорганизующихся систем следует применять методы дискретной математики, разрабатывая на их основе языки моделирования и автоматизации проектирования, и, как правило, - формировать

модель, сочетая методы из групп МАИС и МФПС.

Таблица 2.2

Пикладные классификации методов моделирования	Классификации методов формализованно? представления систем					0
	Анали­тиче­ские	Стати­стиче­ские	Теоре-тнко-множе-ственные	Ло­гиче­ские	Линг­висти­ческие	I ра-фиче-ские
Экономико-
математические
методы
Производственные	+	+
функции
Балансные модели	+
Модели объемного			+
планирования
Модели календарного	+		+			+
планирования (упорядо­
чения во времени, распи­
сания)
Потоковые (транспорт­	+					+
ные) модели
Модели распределения	+
и назначения
Модели управления за­	+	+
пасами
Модели износа и заме­	+	+
ны оборудования
Модели массового		+
обслуживания
Состязательные модели	+	+
Методы работы с
массивами информации
Методы организации			+	+		+
массивов
Методы обработки мас­			+	+
сивов (сортировки, упо­
рядочения, размещения)
Методы поиска инфор­			+	+	+
мации

Следует оговорить, что любая классификация систем всегда мо­жет быть подвергнута критике. Однако, понимая условность клас-

91

сифик^Чии, ее все же нужно создавать. Желательно, чтобы такую классификацию формировал коллектив, разрабатывающий и при. меняющий модель или методику системного анализа. Это позволит ему в (^олее сжатые сроки выбрать методы моделирования для вы. поднеся того или иного этапа методики системного анализа.

Вс^ методы современной математики не может глубоко знать ни один социалист, однако при выборе метода важно понимать осо­бенности того или иного направления и возможности его использо­вания, ^а- выбрав метод, пригласить соответствующих специалистов, владеющих им. Конечно, выбор метода зависит от предшествую­щего с?пыта разработчиков и управленческих работников. Однако необходимо понимать, что ошибки в выборе методов моделирова­ния н^ начальных этапах постановки задачи могут существенно повли^ь ^на дальнейший ход работ, затянуть их или привести в тупик, *тогда решение вообще не будет получено.

Поэтому мы постараемся кратко охарактеризовать выделенные группу¹ методов, обращая внимание на следующие особенности:

основной понятийный, терминологический аппарат методов соот-ветствУещето класса; направления (теоретические и прикладные), котор”^ возникли и развиваются на базе представлений соответ­ствующего класса; преимущества и недостатки методов, области (cibepbf) чх применения и ограничения с точки зрения моделирования сложных процессов и проблем.

Аналитические и статистические методы. Эти группы методов получки наибольшее распространение в практике проектирования и упр^ьления. Правда, для представления промежуточных и окон-чателг"¹¹^ результатов моделирования широко используются гра­фические представления (графики, диаграммы и т. п.). Однако по­следив являются вспомогательными; основу же модели, доказа­тельств ^ee адекватности составляют те или иные направления ана-литич^ких и статистических представлений. Поэтому, несмотря на то, ч1° по основным направлениям этих двух классов методов в вузах читаются самостоятельные курсы лекций, мы все же кратко охарактеризуем их особенности, достоинства и недостатки с точки зрений возможности использования при моделировании систем.

аналитическими в рассматриваемой классификации назвав методы, которые отображают реальные объекты и процес­сы в ^КДв точек (безразмерных в строгих математических доказа­тельствах), совершающих какие-либо перемещения в пространстве или в^имодействующих между собой.

В та⁶'¹¹- 2.1 эт-а особенность аналитических представлений условно иллюстрируй ся сим^Ди^^им обратом, преобразования сложной системы в точку, соверш³ ющую "якое-то движение (или обладающую каким-то поведением), посредство" операт''?³ (функции, функционала) 0[SJ. Как правило, поведение точек, их взаим? действ^ описываются строгими соотношениями, имеющими силу закона.

92

Основу понятийного (терминологического) аппарата этих пред-явлений составляют понятия классической математики (величина, ^„мула, функция, уравнение, система уравнений, логарифм, диффе-

прнциал, интеграл и т. д.).

Аналитические представления имеют многовековую историю

оазвития [2.41, 2.45 и др.], и для них характерно не только стремле­ние к строгости терминологии, но и к закреплению за некоторыми специальными величинами определенных букв (напр., удвоенное отношение площади круга к площади вписанного в него квадрата -я ж 3,14; основание натурального логарифма - е ” 2,7 и т. д.).

На базе аналитических представлений возникли и развиваются математические теории различной сложности - от аппарата класси­ческого математического анализа (методов исследования функций, их вида, способов представления, поиска экстремумов функций и т. п.) до таких новых разделов современной математики, как мате­матическое программирование (линейное, нелинейное, динамическое и т. п.), теория игр (матричные игры с чистыми стратегиями, диф­ференциальные игры и т. п.).

Эти теоретические направления стали основой многих при­кладных, в т. ч. теории автоматического управления, теории опти­мальных решений и т. д.

При моделировании систем применяется широкий спектр сим­волических представлений, использующих "язык" классической ма­тематики. Однако далеко не всегда эти символические предста­вления адекватно отражают реальные сложные процессы, и их в этих случаях, вообще говоря, нельзя считать строгими математиче­скими моделями.

Большинство из направлений математики не содержит средств постановки задачи и доказательства адекватности модели. Послед­няя доказывается экспериментом, который по мере усложнения проблем становится также все более сложным, дорогостоящим, не

всегда бесспорен и реализуем.

В то же время в состав этого класса методов входит относи­тельно новое направление математики математическое программи­рование, которое содержит средства постановки задачи и расширяет возможности доказательства адекватности моделей.

Идея этого направления была предложена инженером, а впо­следствии за работы в этой области лауреатом государственной и нобелевской премий Л.В.Канторовичем [2.19] для решения эконо­мических задач (в частности, - задачи раскроя фанеры'). Эта идея не сразу была воспринята экономистами, но после признания ее за Рубежом (независимо ее предложили и развивали Т.Кукланс и

пксния определяют область.допустимых решении, а наклон прямо”, отчб-^otpa д целевую функцию, определяет точку пошеднего ее пересечения с об-р;,жаЮЧ"" • " ластью допустимых решении, которая

Дж.Данциг, которые признали приоритет Л.В.Канторовича) полу. чила широкое применение в экономике и развивалась рядом у>^ ных, в том числе профессорами Ленинградского политехнического. института В.В.Новожиловым, С.А.Соколицыным, Б.И.Кузиным ц др., и в настоящее время экономику невозможно представить б^ экономико-математических методов, основанных на математич^ ском программировании.

Привлекательность методов математического программирова. ния для решения слабоформализованных задач (каковыми, как пра. вило, являются задачи планирования, распределения работ и ресур. сов, загрузки оборудования и другие задачи управления современ. ным предприятием на начальном этапе их постановки) объясняете) рядом особенностей, отличающих эти методы от методов класси­ческой математики.

Для пояснения этих особенностей рассмотрим упрощенный при­мер.

Предположим, что в трех цехах (Ц1, Ц2, ЦЗ) изготавливается два вида изделй HI и И2. Известна загрузка каждого цеха а, (оцениваемая в данном случае в про. центах) при изготовлении каждого из изделий и прибыль (или цена, объем peamuyi. мой продукции в рублях) с, от реализации изделий. Требуется определить, сколыв изделий каждого вида следует производить при возможно более полной загрузи цехов, чтобы получить за рассматриваемый плановый период максимальную пря-быль или максимальный объем реализуемой продукции.

Такую ситуацию удобно отобразить таблицей 2.3, которая подсказывает xapai-тсрную для задач математического программирования форму представления задачи т. е. целевую функцию (в данном случае определяющую максимизацию прибыли ия объема реализуемой продукции)

я

^Fs ес, ^,==240 л;+320х2-” max, . (2.1)

и ряд ограничений (в данном случае диктуемых возможностями цехов, т. е. их прт дельной 100%-ной загрузкой)

5 х, + 4л, <ioo

Таблица 2.3 1,6 х, + 6,4 х: < 100 W 2,9xi + 5,8 ^< 100

Изделия

Цех (участок)

Цена изделия

		т		Ц2	ЦЗ

И1	5%	1,6%	2,9%	240 руб.
И2	4%	6,4%	5,8%	320 руб.
Макси­мальная загрузка	100%	100%	100%

В данном случае ограничен” однородны и их можно записав короче:

(2.2а)

В общем случае может бьЛ* несколько групп подобных огр'' ничений (например, по имеюШЧЧ ся материалам разного вида, себестоимости, заработной плате рабочих и т. п.).

Графическое решение задачи приведено на рис. 2.4. 94

и является наилучшим решением задачи (оптимумом). В данном с;|\чае .v,=y, .^=13."

I) случае оо.тьшею числа рашо-рйдных ограничении |рафичсск;1я ин­терпретация задачи затруднена, по­этому используются специальные ме­тоды (например, симплекс-метод), па­кеты прикладных программ, их реа­лизующие. В зависимости от вида пе.тевой функции и принципов орга-ilinauiui решения выделяют направ-.1С1И1Я математическою программи­рования: линейное (при лчнеином ха-p.iKicpcucaiCHoii функции), ш-.штйчче (пс-юная функция iic.iilHcilii.i): цг.ю-чиглгннм (ограничение на харяктар

НСрСМСПНЫХ). l4lllllUU4t4Kl'r И Т П.

2>lil нанран-юнни hmcict чюннфнчс-л-не осоОснносгн ч мсюды решения [5, 11 Я, г.2.\ ?.?(”, 2.33, 2.37, ;.4:, 2.43 и .ip ]. 11.. чсновная суть пжчановкн •ia<ia4il счхраихэтси.

Анализ хода постановки и решения задачи позволяет выявить основные особенности математического программирования:

введение понятий целевая функция и ограничения и ориентация на их формирование является фактически некоторыми средствами постановки задачи: причем эти средства могут использоваться даже если не удается сформировать систему непротиворечивых ограни­чений или записать целевую функцию в формальном виде, посколь­ку удается уточнить представление о проблемной ситуации и, таким образом, поставить задачу хотя бы в первом приближении;

при использовании методов математического программирова­ния появляется возможность объединения в единой модели разно­родных критериев (разных размерностей, предельных значений), что очень важно при отображении реальных проектных и производ­ственных ситуаций:

модель математического программирования допускает (и даже ориентирует на это) выхоо на границу области определения перемен­ных (в то время, как методы классической математики требуют вве­дения строгих начальных и граничных условий, значений которых не может принимать переменная в процессе анализа модели);

изучение методов решения задач математического программи­рования позволяет получить представление о пошаговом прибли­жении к решению, т. е. о пошаговом алгоритме получения резуль­тата моделирования;

графическая интерпретация задачи дает наглядное представ­ление об области допустимых решений (которая на рис. 2.4 за-95

штрихована), что помогает в практических ситуациях даже в т случаях, когда не удается получить формальное отображение левой функции и строго решить задачу математического програ¹ мирования.

Благодаря рассмотренным особенностям методы математик ского программирования можно кратко охарактеризовать как щ, тоды, имеющие в отличие от классической математики некоторц, средства постановки задачи. В частности, термин целевая функцц часто используется даже в тех случаях, когда очевидна невозмо” ность формального установления детерминированных взаимосвязи между компонентами и целями системы. Помогает в постановке з” дачи и понятие области допустимых решений. Этим объясняется по пулярность рассматриваемого направления: однако получаемые] таких случаях модели уже не будут относиться к моделям математ” ческого программирования и к аналитическим методам.

Резюмируя, еще раз обратим внимание на то, что аналитически методы применяются в тех случаях, когда свойства системы мощ” отобразить с помощью детерминированных величин или зависимо стей, т. е. когда знания о процессии и событиях в некотором инта вале времени позволяют полностью определить поведение их вне зп” го интервали. Эти методы используются при решении задач движ ния и устойчивости, оптимального размещения, распределения pi бот и ресурсов, выбора наилучшего пути, оптимальной стратеги поведения, в т. ч. в конфликтных ситуациях и т. п.

В то же время при практическом применении аналитически представлений для отображения сложных систем следует иметь' виду. что они требуют установления всех детерминированных сш зей между учитываемыми компонентами и целями системы в вид аналитических зависимостей. Для сложных многокомпонентны! многокритериальных систем получить требуемые аналитические 31 висимости крайне трудно. Более того, даже если это и удается, и практически невозможно доказать правомерность применения т ких выражений, т. е. адекватность модели рассматриваемой задан. В таких ситуациях следует обратиться к другим методам моделирс вания.

Статистические представления сформировались и самостоятельное научное направление в середине прошлого ве” (хотя возникли значительно раньше* ). Основу их составляет ото( ражение явлений и процессов с помощью случайных (стохастич ских) событий и их поведений, которые описываются соответств;

ющими вероятностными (статистическими) характеристиками статистическими закономерностями.

„I 'стохастические" уточняет понятие "случайный", которое в обыденном принято связывать с отсутствием причин появления событий, с появлением '"''""^ько повторяющихся и подчиняющихся каким-то закономерностям, но и еди-^м а событий: процессы же, отображаемые статистическими закономерностями. ничяь" ^^ жестко связаны с заранее заданными, определенными причинами, а ^"айность" означает, что они могут появиться или не появиться при наличии Энного комплекса причин.

Статистические отображения системы в общем случае (по ана­логии с аналитическими) можно представить (см. символический образ в табл. 2.1) как бы в виде "размытой" точки (размытой об­ласти) в я-мерном пространстве, в которую переводит систему (ее учитываемые в модели свойства) оператор <I>[SJ. "Размытую" точ­ку следует понимать как некоторую область, характеризующую движение системы (ее поведение); при этом границы области заданы с некоторой вероятностью p^\ ("размыты") и движение точки описы­вается некоторой случайной функцией.

Закрепляя все параметры этой области, кроме одного, можно получить срез по линии а - Ь, смысл которого - воздействие данно­го параметра на поведение системы, что можно описать статистиче­ским распределением по этому параметру. Аналогично можно по­лучить двумерную, трехмерную и т. д. картины статистического распределения.

Статистические закономерности можно представить в виде дис­кретных случайных величин и их вероятностей, или в виде непре­рывных зависимостей распределения событий, процессов.

Для дискретных событий соотношение между возможными значениями случайной величины х, и их вероятностями р, назы-Таблчца2.4 вают законом распределения и ли­бо записывают в виде ряда (табл. 2.4), либо представляют в виде зависимостей F(x) (рис. 2.5 а) или

х	Xt	Х2		х!		^
Р(х)	Р'	Р2		Pi-		Рп

P^i) (рис. 2.5 б). При этом

F(x)= Z р^х,). (2.3)

Для непрерывных случайных величин (процессов) закон распре­деления представляют (соответственно дискретным законам) либо в виде функции распределения (интегральный закон распределения -рис. 2.5 б), либо в виде плотности вероятностей (дифференциаль­ный закон распределения - рис. 2.5 в). В этом случае р(х)= dF(x)/dx и ^F(x) = р(х) Лх, где р(х) - вероятность попадания случайных со­бытий в интервал от х до х+Ах.

Для полной группы несовместных событий имеют место условия нормирования:

закона распределения

(2.4)

(2.4a)

и плотности вероятности

00

J p(x)dx = F(oo) - F(-oo) =1-0=1

В монографиях и учебниках применяют тот или иной вид зави­симостей, приведенных на рис. 2.5, более подходящий для соотвег. ствующих приложений.

F(x)

“)

р(х)

Х, Хг Xi X: Х{ -t(+A'c, x

Рис. 2.5

Закон распределения является удобной формой статистического отображения системы. Однако получение закона (даже одномерно­го) или определение изменений этого закона при прохождении через какие-либо устройства или среды представляет собой трудную, ча­сто невыполнимую задачу. Поэтому в ряде случаев пользуются не распределением, а его характеристиками - начальными и централь­ными моментами.

98

Наибольшее применение получили:

1-й начальный момент - математическое ожидание или среднее значение случайной величины

т^ = £ х,р,-(х,) - для дискретных величин ,

(2.5)

OU

= [ р(х) dx - для непрерывных величин;

2-й центральный момент - дисперсия случайной величины:

п

о^ =T,(Xf - ту pi(Xi) - для дискретных величин;

(2.6)

OD

<г,² = [ (x - т^Ур^х) dx - для непрерывных величин.

На практике иногда используется не дисперсия о^², а среднее

квадратаческое отклонение (Ту

Связь между системами в общем случае характеризуется кова-

риацией - моментом связи; для двумерного распределения обозна­чаемых cov(x,y), или/Иду, или М[(х -т^)(у -ту)].

Можно использовать ковариацию нормированных отклонений -

коэффициент корреляции

(х-т^)(у-ту)

г = cov(x', у)= М [——————————1, (2.7)

0,0^,

где x' = (x - w^)/CT(, у'=• (у -т^Оу - нормированные отклонения;

с^, ay - среднеквадратические отклонения.

Практическое применение получили в основном одномерные распределения, что связано со сложностью получения статистиче­ских закономерностей и доказательства адекватности их примене­ния для конкретных приложений, которое базируется на понятии

выборки.

Под выборкой понимается часть изучаемой совокупности явле­ний, на основе исследования которой получают статистические за­кономерности, присущие всей совокупности и распространяемые на нее с какой-то вероятностью.

Для того, чтобы полученные при исследовании выборки закономерности мож­но было распространить на всю совокупность, выборка должна быть представи­тельной (репрезентативной), т. е. обладать определенными качественными и коли-99

чественными характеристиками. Качественные характеристики связаны с содержа. тельным аспектом выборки, т. е. с определением, являются ли элементы, входящие в выборку, элементами исследуемой совокупности, правильно ли отобраны эти элементы с точки зрения цели исследования (с этой точки зрения выборка можд быть случайной, направленной или смешанной). Количественные характеристики представительности выборки связаны с определением объема выборки, достаточно­го для того. чтобы на основе ее исследования можно было делать выводы о совокуп­ности в целом; уменьшение объема выборки можно получить на основе эргодтеско. го свойства, т. е. путем увеличения длительности статистических испытаний (в боль. шинстве практических случаев вопрос о количественных характеристиках выборка является предметом специального исследования).

На базе статистических представлений развивается ряд матема­тических теорий: математическая статистика [7, 2.9, 2.64 и др.], объединяющая различные методы статистического анализа (рег­рессионный, дисперсионный, корреляционный, факторный и т. п.)';

теория статистических испытаний, основой которой является ме­тод Монте-Карло, а развитием - теория статистического ими­тационного моделирования; теория выдвижения и проверки статис­тических гипотез, возникшая для оценки процессов передачи сиг­налов на расстоянии и базирующаяся на общей теории статисти­ческих решающих функций А.Вальда [2.8] (частным случаем теории выдвижения гипотез, важным для теории систем, является байесов­ский подход к исследованию процессов передачи информации в процессах общения, обучения и др. ситуациях в организационных системах”; теория потенциальной помехоустойчивости, начала ко­торой положены работами В.А.Котельникова [1.27], проводимыми независимо от теории решающих функций; обобщающая последние два направления теория статистических решений, в рамках кото­рой, в свою очередь, возник ряд интересных и полезных для прак­тики направлений.

Перечисленные направления в большинстве своем носят теоре­тико-прикладной характер и возникали из потребностей практики. Однако есть и ряд дисциплин, которые носят более выраженный прикладной характер. В их числе - статистическая радиотехника, статистическая теория распознавания образов, экономическая ста­тистика, теория массового обслуживания; а также развившиеся из направлений, возникших на базе аналитических представлений, -стохастическое программирование, новые разделы теории игр и т. п.

Расширение возможностей отображения сложных систем и про­цессов по сравнению с аналитическими методами можно объяснить тем, что при применении статистических представлений процесс постановки задачи как бы частично заменяется статистическими исследованиями, позволяющими, не выявляя все детерминирован-

связи между изучаемыми объектами (событиями) или учиты-^ны мыми компонентами сложной системы, на основе выборочно-^0а исследования (исследования репрезентативной выборки) полу-^г0 ь статистические закономерности и распространять их на пове-

^ние системы в целом.

Однако не всегда можно получить статистические закономер-ости, не всегда может быть определена репрезентативная выборка, ^н казана правомерность применения статистических закономерно­стей. Если же не удается доказать репрезентативность выборки или для этого требуется недопустимо большое время, то применение статистических методов может привести к неверным результатам.

В таких случаях целесообразно обратиться к методам, объеди­няемым под общим названием - методы дискретной математики, которые помогают разрабатывать языки моделирования, модели и методики постепенной формализации процесса принятия решения.

Понятие о методах дискретной математики. Характеризуемые ниже методы возникали как самостоятельные направления и перво­начально развивались параллельно и независимо друг от друга. Но обобщающий аппарат теоретико-множественных представлений оказался настолько удобным средством пояснения основных поня­тий, а часто и доказательства теорем в математической логике, ма­тематической лингвистике и даже в теории графов, что постепенно все эти методы стали объединять в единую область - дискретную математику.

Необходимость в использовании методов дискретной матема­тики возникает в тех случаях, когда алгоритм, который всегда в конечном итоге желательно получить для обеспечения повторяе­мости процесса принятия решения, не удается сразу представить с помощью аналитических или статистических методов. В этих слу­чаях теоретико-множественные, логические, лингвистические или графические методы помогают зафиксировать в алгоритме опыт или эвристики ЛПР.

В принципе для отражения в алгоритме эвристик допустимы любые неформальные отображения. Однако такие эвристические алгоритмы широкого класса - от ГСП-алгоритмов (ГСН - "грубая сила и невежество") до "хитрых", "жадных" и т. п. алгоритмов (название их соответствует виду эвристики, определяющей способ борьбы с перебором при моделировании решения) - часто оказы­ваются далеко неэффективными, а в ряде случаев не существует алгоритма, который позволил бы получить решение не только с наименьшей трудоемкостью, но и вообще в обозримые сроки. И ЗДесь большую помощь в предварительной оценке реализуемости алгоритма, во введении некоторых формальных правил преобразо­вания, позволяющих применить ЭВМ и ускорить получение реше-"чя, могут оказать методы дискретной математики.

101

Практики и инжв*¹^" ^111С Я1°бят изучать процесса получения формул и методов теоремы и тем более ^1СС Д^азательства. А книги по декретной математике написа. ны как правило, с ^я^^^ванием специфических символов и приемов, отличньц от классической мат^^*⁸"™'"'¹' ^к которым мы привыви в школе и в традиционньв курсах высшей мате”*⁸™*^{11 для} вузов. В специальна монографиях и даже в учеб. никах по теории ^^н^ly71iecтв' математической логике ” математической лингвистщ;

обычно вводятся си”***⁰™¹'^{3 и} правила преобразовании довольно длительное врем( рассматриваются во'”¹'¹⁰*"⁰¹-'™ ^этих правил, доказьнаются соответствующие теоре. мы без иллюстрации ир^^гаческой потребности в ни В то же время при утилитар. ном подходе к математике знание доказательств вячего не добавляет к знанию результата: важно энЯ'"'- ^чтц и ^зaчl'^м применять.

Поэтому для прй*^³^¹¹¹¹'¹* ^целеи удобны справочные материалы, являющиеся как бы "выжимками" из oeinHpMoit литературы по дис”ретной математике, что мы ц пытаемся сделать lU*^{жe в} Ф^рме таблиц, в которых собраны основные отношения теории множеств фУ***¹⁰¹*^{1 м} теоремы математической логики и т. д. В ряде случаев такие таблицы moi-у*' ч⁰”*⁰'"' в выборе метода моделирования и в более глубоком ознакомлении с сооТР^"^⁸^¹¹⁰¹¹^⁰¹¹ направлением дисиретной математики.

Кроме того в обЛ²⁰⁷¹¹ Управления, проектировав”! сложных технических и про­изводственных коми⁰"'"'" ^{все 11аше} главной проблемой становится создание прнв. цилиально новых, lle'^l"^pивlla'^ьныx моделей, не по аналогии. В таких случаях матема­тика нужна уже не Л/"¹ вч^чра готового метода pacwa, а как средство мышления,

формирования понят**"-

Такое владение (“•^'"-''^'"'Икой, в том числе и дискрпной, требует более глубокого понимания сути меТ^Д⁰"- Умения оценить, какой из истодов лучше подходит дм формирования моде^* ^в конкретной ситуации. Поэтому, разумеется, излагаемое ниже следует рассматривать. лишь как введение в сложный мир дискретной матема­тики которое имеет целью облегчить изучение специальной литературы.

Некоторые понятия •'^"м несколько подробнее только для того, чтобы были по­няты прикладные прю*еры в последующих главах, позволяющие проиллюстриро­вать возможность iif^K^^nwwi одной и той же задачи несколькими методами и помочь студентам п^”*""¹¹ "Ноблему выбора методов моделирования сложных систем и проблемных cirryatA™ ^с начальной неопределеннопмо.

Изложенное по”*⁰*"" ^кже несколько углубить сравнительный анализ M<P11L, приведенный в табл- ²-¹- вторую следует перечитал, после ознакомления с мате­риалом данного разА®¹'¹' ^а -Чучше - и с обращением к рекомендуемой литературе, на основе которой в учебном процессе и в рамках НИРС студентам целесообразно рекомендовать по.ПГ⁰™¹"^' рефераты, обзоры литературы по рассматриваемым ниже направлениям ДИ^Ф^ой математики.

Teopemttl^co~^мнoжecmвeнныt представления-

Теоретико-мнохс^¹'™®¹*"¹'^ представления базируются на понятиях множество эл^**^""¹¹'* множества, отношения на множествах.

Понятие миоУ^^"¹⁹⁰ относится к числу интуитивно постигаемых понятий, которь*" трудно дать определение. Это понятие содержа­тельно эквивалентно понятиям "совокупность", "собрание", "ан­самбль" "колле*сиия", "семейство", "класс" я другим обобщающим

ПОНЯТИЯМ.

Один из ос^^ч^ложников теории множеств' Георг Кантор определял мнозк⁶⁰"^{0 как} "многое, мыслимое нами как единое".

Множества могут задаваться следующими способами:

1) списком, перечислением (интенсиональным путем);

например,

{а,}, где ('= 1...П, (2.7)

или

<а„ а:,... , а„ — , а„> , (2.7а)

где а, е А , е - знак вхождения элементов в множество;

2) путем указания некоторого характеристического свойства А (экстенсионально). Например, "множество натуральных чисел", "множество рабочих данного завода", "множество планет солнечной системы", "множество А" и т. д.

В основе теоретико-множественных преобразований лежит принцип перехода от одного способа задания множества к дру­гому:

А = <а„ а^ ... , а„ ... , а„>, (2.8)

или

<а/, а;,... , а„ ..., a„> ->A. (2.8а)

Переход от интенсионального способа задания множества к экстенсиональному называют принципом свертывания.

В множестве могут быть выделены подмножества. Вхождение элементов в любое множество или подмножество описывается зна­ком принадлежит - е, а вхождение подмножества в множество за­писывается В с А. Это означает, что все элементы подмножества В являются одновременно элементами множества А (рис. 2.6):

Ь, е В Ь^ еВ

Ь, еА Ь^е А

ВсА

Ь„еВ

Ь„е А

Рис. 2.6

Важным понятием является понятие пустое множество - мно­жество, в котором в данный момент нет ни одного элемента: D =0.

При использовании теоретико-множественных представлений в соответствии с концепцией Кантора можно вводить любые отноше­ния. При уточнении этих отношений применительно к множествам удобно пользоваться наглядными диаграммами Эйлера-Венна, примеры которых для операции объединения (U ), пересечения (& или о), дополнения (отрицания, обозначаемого знаком "-" над именем множества, либо знаком "-i" перед именем множества или

sro элемента) приведены в табл. 2.5.

[03

Теории, развивавшиеся на б>а;

ставлений. первоначально исгп^едр^^^д^^денных др^ функциям алгебры логики, и )В Ковали отношения, подобны;

логики Буля (приводимые ниже в •^^ очередь - бинарной алгебра

В большинстве работ [2.6, 2.10. 2. 151^f1- ²-")-представления излагаются на примерев ^ ^ ^оретико-множесгеенни, точно основных элементарных отноше.ни ^ ^^ развитая которой дост

По мере приложения теоретико-Mrf⁰^'

проблемам отношения начинают заим!⁰¹”!^ ^в' ^с'^сг" ^с' '"'' '"''^->' .. , , .,„„ I тенных представлении к более сложныь (которую теория множеств, в свою oqiepA'"-""""¹ "f-" - ' " , „ ^ ———— , ..„Тться из математической лингвистики нии особо сложных проблемных ситуаШЧ i '""' " 1, ., ,. .„„к

исследуемую систему отображают мно^. ^{помогает} Р³”"⁸^). ^а при отображ.. (так. например, при применении тсор.стЛ"е"иределенностъю формируемую щ

ционном моделировании используй \ ми с отношениями произвольного та,, "находиться рядом" и т. п., которые Д"у множественных представлении в cm,.. этой основе языке моделирования про.из„'.та"™ния быть над быть под-^t |hiMo обозначать в разрабатываемом а

г^ е- во ^чыми символами, удобными для Л ПР), Особого внимания заслужив

установления взаимоотношений (преобразование множеств путе” ных множеств, 'ежду элементами разных исход. Из двух или нескольких m^o(.

установления отношений меж^У^тв можно сформировать путец множество. Это новое множес:-") ^ементами этих множеств нова вать как множество, состоящей и ^ ^ правило, следует рассматри. „ „ ,., Принципиально новых элементов.

Например, объединяя элементы И''1| ^г "катушки индуктивности L", получ^”¹ ^ „ > .-,, ^•(если, конечно, введенное отноше-ии^¹^¹'³ '^е^аторь. С и множен необходимые действия по объединению^⁰⁶ множеспю колеб.апиьньи- контур катушек индуктивноста). Аналогичны ^, ежду исходными элементами отображая из множеств "женихи Г' и "невесть, tf" ч^тветствующих выводов конденсаторо”

(процедуры ротации брака)^фоР^сГЙТГоо^^^^^^^

рого с, =<у, г, g,>. где у, е ), g,: ё ^ \ множество -Семьи С', элементы кст

между людьми, имеющих принципиальн ,\ ^ ^ ^ _ ^^ство взаимоотношеш.

.-г ,. овый смысл для общества.

При этом важно отметить. \

либо вида специальных отно^е^ ^ только установление какого pax, но и формирование элем^н^ ^3^ g ^^ приведенных прим^ стого "помещения рядом" элеме^д нового множества путем пр& получать эффект появления н^дд исходных множеств позволяе' доосмыслениемвзаимоотношен^^д смысла, что обеспечиваете! ствующего опыта. Это важно п^ человеком на основе его преди” шой исходной неопределенн*?^ моделировании ситуаций с бол имоотношений между элемента ^^ неизвестен характер вз выявленных для отображения Cfy\^ разных групп (подмножест! эффект будет использован в цо^ ^^ проблемной ситуации. Эт нии процесса структуризации Ч^дующих главах при моделиро! моделировании (гл. 7). ^ ^д 4), при морфологической

104

При пспольи.вачип таких iipcoupa'”¹¹'-¹¹¹¹¹" нсооходимо предварительно оцени. Hail.licpa-.op.llpllllo.ivHclllllnioBoloMll"*^™” l" vicmcutob 2-х. 3-х ч-ш полк исходных подмножеств с 'Дэтсмагическг!¹ """'ч 'Р""¹" "^{месг мссто} "чер-шчя рш .чгн”1-"ия с ттюрепчями. при Исиодыоч'""'" коюрон ччсю получаемых комчопги-юн

k-=A,.A-'-*^ • <^

“дсА-, А-,.... .А-,-количества ..icMemol”* •¹^ ^л/;. • •"" подмножествах. то. даст существенно меш.пши нсреоор. чем формирование сочетании.'

Между теоретико-множест^нкыми описаниями разных систем или их частей можно устанавливать соответствия. Для характери­стики сходства множеств (подмножеств) можно использовать поня­тия гомолюрфими. июморфимч мтоморфтма. отношения рефлек­сивности. счм.иетричпм-пш. тр^^ччностч. заимствованные тео­рией множеств из других раздел⁰" математики.

для отображения систем важными понятиями являются понятия ординарного и птпчаординарчого множеств. Если множество сформировано из геометрических АигУР - например, треугольников, - и принято условие, что формирование нового 'тожества осуществляется в той же плоскости, то полученное новое множество будет также плоской геометрической фигурой, а, возможно даже и треугольником. Такие множества относят к классу ординарных. Аналогично можно посмот-пегь на множество колебательных контуров, которые так же, как конденсаторы и 'тупоси индуктивности, являются элементами радиотехнических устройств.

Однако, учитывая принципиально новые свойства колебательного контура, мож­но эту же ситуацию трактовать как формирование экстраординарного множества с принципиально новыми свойствами элементов. При формировании экстраординарного множества в примере с семьей изменяются не только свойства множества, но и суть и даже наименования исходных элементов ("жених" - "муж", "невеста" - "жена").

Важным понятием для освоения и использования теоретико-множественных представлений является понятие континуума (от ла­тинского "continuum" - "непрерывный") - связного обобщающего множества (т. е. как бы единого непрерывного пространства), в рамках которого осуществляются операции над множествами (их изъятие, добавление новых, объединение, пересечение и т. п.).

В простейших случаях континуум может быть задан границей, которая не изы­мается даже в случае, если исключаемое множество (подмножество) вплотную смы­кается с этой границей (в примерах, приведенных в таблице 2.5, роль континуума играет прямоугольник). Роль континуума может играть пустое множество, значи­тельно больших потенциальных размеров, чем входящие в него подмножества. Но в более общем случае (особенно при отображении открытой системы, в которую могут постоянно включаться новые подмножества с непредсказуемыми границами) кон­тинуум формируется как внешняя граница всех пересекающихся или другим образом взаимодействующих подмножеств, с помощью которых отображается система.

Понятно, что в случае моделирования развивающихся систем континуум посто­янно видоизменяется, и его изменения, в т. ч. сохранение связности, нужно посто-ямо уточнять.

Благодаря тому, что в соответствии с первоначальной концеп­цией Кантора при применении теории множеств допустимо введе­ние любых произвольных отношений, теоретико-множественные представления стали использоваться как обобщающий язык при сопоставлении различных направлений математики и других дисци­плин, явились основой для возникновения новых научных направ­лений или развития существующих.

В частности, теоретико-множественные представления получили широкое рас-"Рвстраненис для уточнения ряда математических направлений (первой теорией, для которой на основе этих представлений были получены важные новые результаты, была теория чисел); сыграли большую роль в становлении комбинаторики, топало-^гии, в разработке теории "размытых' множеств Л.Заде [3.7]; на их основе стали издаваться первые информационно-поисковые языки, языки автоматизации моделыро-"wuv, на теоретико-множественных представлениях базируется вариант математи-^кой теории систем М-Месаровнча [4).

107

Использование теоретико-множественных представлений пп моделировании систем позволяет организовать взаимодействие " взаимопонимание между специалистами различных областей зц, ний. С их помощью можно записать различные определения си стемы (что делалось в гл. 1) и выбрать из них то, которое в нац. большей степени отражает концепцию исследователей, проект^ ровщиков.

Конкретная система при первоначальном описании может бьщ отображена теоретико-множественной формулой, включающей на. боры различных элементов (например, А, В, Q, отношений между ними (R), которые могут быть также разделены на подмножества (/?!, /?2, Rs и т. д.), свойств элементов бд, Q^, Qc и свойств отноцц. ний Q/, могут быть учтены множества входных воздействий X ц выходных результатов У:

(2.10)

S = <А, В, С, R, б„, а, б,, б„ X, Y>.

Затем, по мере накопления сведений о системе, теоретико-мно­жественная формула (2.10) может измениться и отразить взаимо­отношения между группами множеств:

S=<{x.}Ri {а,}Р1{Ь^}Рз{с,}>, (2.11)

а в дальнейшем описание может уточняться: могут быть введены подмножества и отношения между ними и их элементами; деление на подмножества может быть повторено неоднократно, и таким об­разом с помощью теоретико-множественных представлений может быть отображена многоуровневая структура; отношения могут быть уточнены в виде набора правил преобразования множеств или подмножеств.

Как уже было сказано выше, при использовании теоретико-множественных представлений в принципе можно вводить любые отношения. Однако при произвольных отношениях в формализо­ванном с их помощью описании проблемной ситуации довольно быстро могут обнаружиться неразрешимые противоречия - пара­доксы, апории или антиномии, что не позволяет оперировать с по­лучаемыми теоретико-множественными моделями таким же обра­зом, как с классическими математическими соотношениями, и до­верять достоверности получаемых результатов.

В качестве примеров парадоксов приводят обычно: парадокс лжеца (нельзя дать положительного ответа на вопрос "Ты лжешь?");

парадокс парикмахера, которому отдано распоряжение "брить всех мужчин в полку, которые не бреются сами".

Действительно, если попытаться формально записать ситуацию парадок" парикмахера, то возникает неразрешимое противоречие: парикмахер Х приная^ жиг множеству одновременно мужчин Mi, которые не бреются сами и которых п°

108

яжекию он обязан брить, и множеству тех мужчин Мг, которые бреются сами '""ооьв согласно распоряжению он брить не должен, и эти множества М\ а М-г ^и """ресекаются и не входят друг в друга, т. с. должно иметь место: Х е A/i, X e Mi. ^не \ ^, U А^ = 0 . что невозможно.

С примерами антиномий можно познакомиться, например, в популярной брошюре Н.Я.Виленкина [2.10], в которой наряду с эвестными парадоксами приводятся ситуации возможности полу­чения при применении теоретико-множественных представлений "безразмерных гостиниц" лемовского героя Иона Тихого.'

Примеры парадоксов легко можно найти во многих высказываниях неформали-•юванного текста: например, "Ты должен сам любить меня" (если "должен", то "не пди"; если "сам" - то никому ничего "не должен").

На этом свойстве текстов основаны некоторые психологические тесты. Эта поивципиальная особенность текстов не позволяет однозначно отразить с их по­мощью проблемные ситуации и требует перевода текстов в формализованные опи­сания с использованием специализированных знаковых систем, языков, в которых по возможности устранены парадоксы. Для разработки таких языков могут быть использованы теоретико-множественные представления, которые позволяют выяв­лять и устранять парадоксы, ограничивая при этом свободу выбора отношений,

т. е., строго говоря, огрубляя качественное описание, уменьшая его полноту. Однако тате ограничения при применении теоретико-множественных представлений мож­но делать осознанно, фиксировать и пересматривать при необходимости. При раз­работке языков моделирования полезно ознакомиться с конструктивной теорией множеств (см., например, в [2.20D.

Математическая логика. Базовыми понятиями ма-тематическоГ- логики являются высказывание, предикат, логические функции (операции) кванторы, логический базис, логические зако­ны (законы алгебры логики).

Под высказыванием в алгебре логики понимается повествова­тельное предложение (суждение), которое характеризуется опреде­ленным значением истинности.

В простейших случаях используется два значения истинности:

"истинно" - "ложно", "да" - "нет", "1" - "О". Такая алгебра логики, в которой переменная может принимать только два значения истин­ности, называется бинарной алгеброй логики Буля (по имени соз­дателя алгебры логики).

Предикат - выражение, грамматически имеющее форму выска­зывания, но содержащее переменные некоторых подмножеств, на которых они определены.

При замене переменных элементами соответствующего подмно­жества предикат обращается в высказывание. Обычно переменная ^оит в предикативной части предложения, лежащего в основе вы-^азывания (например, "быть A'-вым карандашом", где Х может "Ринимать значения "красным", "синим" и т. д.), но в принципе это

	Логические		Лоппеаяе оперших (фунтик. ^~~"'
	аргу”	центы
способы	а	Ь	Fl.O	Рг-1	F”-a	F4-b	F5~avb tub	РсчлЬ “^ь	г^ м;
алгебраической							i+b	аАЬ	“Kb
залиси								”ь	tah
логического								>хЬ
отношения
аргументов с
функцией
Двоичная форма	1	1	0	1	1	1	1	1	т^^
записи связи	1	0	0	1	1	0	1	0
воздействия с	0	1	0	1	0	1	1	0	5
результатом	0	0	0	1	0	0	0	0	1
Основные	Пер­	Вто­	Тож­	Тож-	ут-	Утвер	Ди-	Ко-	ЭщЙ-
встречающиеся	вое	рое	дест­	дест-	вержде	жде-	мяю.-	кыонхц	лет.
в литературе	логи­	логи­	вен-	векки	нке	нне	шт.	их.	носи
названия	чес­	чес­	HUM	едини­	пер­	второ­	Лога-	Логи-	Гта.
логической	кое	кое	нуя”.	ца	вого	го	чеаая	чеаое	т-
функции	воз­	хо-	Тож­	Тож­	apry-	аргу­	сумм”.	прою-	косп
(операции,	дейст­	дейст­	дест­	дест­	мекп	мента	Овм-	всде-	М.те.
фактора)	вие.	вие.	венно	венно	(пере­	(пере­	диме-	нне	рталь.
	Пер­	Вто­	ложно	истин­	менно-	маню	нке	Пере­	ни
	вое	рое		но	ГО.ВОЭ-	го,	Прос­	числе­	тт.
	логи­	логи­			деЯст-	ВОЗ-	тая	ние.	пап-
	чес­	чес­			внж)	ДсЙСТ-	(нераз-	Совгад	носп.
	кое	кое			Пов­	ВИЯ)	Делн-	екке.	Bum.
	пере­	пере.			торе­	Повто	тель­	Соеди­	носп.
	мен­	цен­			ние	рснне	ная)	ненное	Соли.
	ное.	ное.			пер­	второ­	ди­	сужде­	яр-
	Пер­	Вто­			вого	го	зъюнк­	ние.	носп.
	вый	рой			аргу­	аргу­	ция	4>стио	Ком”
	логи­	логи­			мента	мента	Сбор-	утвср-	матр
	чес­	чес­			(пе­	(пере­	хя.	дителш
	кий	кий			ремен­	мен­	Абстра	ое	Ихтер-
	аргу­	аргу-			ного)	ного)	гнро-	сужде­	делен.
	мент	мент			Доми-	Доми-	вшие.	ние.	денди
					кацня	каоня	Комби	Реали-
					пер­	второ­	кацкя.	эова-
					вого	го	Асто-	ние
					пере­	пере.	номих.
					менно­	мекко	Коне-
					го	го	телля-
							цкя
Условные названия логических функций			Любое ложно	Любое истки 0	Kara	КахЬ	н/нлн хотя бы	И И И	Ki”

Таблиц” 3.6

фиторы, отношенх”)

-FrST"	~~fw'b v^b	Flo-*/b ^b	Fll-a*b ”<Ь	Fn-a<b acb	Fl3- a -•а	Fl4- b -^ь	Fll-a\b аЙЬ	Рк-ая ас
>-”ь	av b	лЬ	авЬ	а<-Ь	а*	b'	а5Ь	а ^
“>ь		•Ь	а“Ь		-а	-b	а-”Ь
		хЬ	•ЛЬ		-.с	-0°
		ЛЬ			-са	-cb
0 1	0 0 0	1	1 1	1 0	0	0	1 0	0 1
1	1	1	0	1	1	1	0	0
Имплюа шм.	фучияч Вэво”.	Шеффера.	цакне	Обрат­ная	Отри­цание	Отри­цание	кие	цание
Саяо-	Опера­	Операцнх	равноз­	кмплкхя	первого	второго	мате­	обрат­
мяк.	ция	Шсффер^	начности	цкя.	аргу­	аргу­	риаль­	ной
Мве-	Пнрс”.	Штрих	Фуикцкя	Обрат­	мента.	мента.	ной	кмллнк
уиа-	Огрк-	Шеффера.	ражон-	ное	Икверта	Инверта	кмллнка	ция
ml	юкие	Отрнюике	менкос-	следо­	цкя пер­	цня	цки.	Обрат­
яями-	ДГО1ЮНГ	хокыоях-	тн.	вание.	вого	второго	Мате­	ная ант
WL	цки.	цкк	Фунжцкя	Обрат­	аргу­	аргу­	риальная	нмллиж
Обще.	Обутая	Обрхтжя	сложе­	ная	мента	мента	анти-	ция
уперДИ-	дюыонх	кяажяа.-	ния по	селехцш	(пере­	(пере­	иыллнкв	(неимп
таыюе	IOU.	им.	модулю	Обрат­	менного)	менного)	ция.	ккацкя
суж“е-	Ангн-	Неххяшоих	2.	ная	Допояне	Допояне	Анти-	Обрат­
мк.	дкхыокг	цкх.	Нерш-	слецифи	киек	ниек	совпаде­	ное
Сокх-	ша	Обратное	кознхчн	кация.	первому	второму	ние.	разде­
“п	Обрспоя	логкчесхве	ост”	Обрат­	пере­	перемен	Разде­	литель
СЛЕЦКФИ	логи­	произведе­	Строгая	ная	менному	ному.	литель­	нос
аща	ческая	ние	дкпюю;	детерми	Профа.	Обрат­	ное	сужде­
Дстерми	сумма.	Обратное	цш.	каиня.	же	ный	сужде­	ние.
ишт.	Гстсрофа	совпадение.	Исклю­			сигкфа-	ние.	Обрат­
Обраткы	эяс.	Альтерна­	чающая			знс.	Отри­	ное
waoaci-	Неди-	тивное	дюыонх				цание	анти­
лоацкя	гъюмх'	отрицание.	цкя.				селещкн	совпа­
	ЦКЯ.	Несовмссгн	Раздели­				Антисе-	дение
	Отршс-	мосп	тельная				лекикя.
	кие	Общеотри­	дхзьюкх				Актиспе
	комби”	цательное	цкя.				цифиха-
	ции,	суждение	Отрица­				IOU
	автономм		ние				Антиде-
	КИ.ТЛ		взакмоэа				термкка-
	Актн-		внснмос.				цня
	констеях		ти
	ция
Ева то Только	Не или Ни ни	Ней Илмие	Не пах Или и”	Или не	Не”	Heb	Ноне	Йене

"S^n¹³"^"^}^{11 возможны} "Ред"^™ ".Г- река", где Х -"Волга",

или я^кольки^е^е^*'¹¹"'¹ является пропозиционная функция - функция одной или нескольких переменно принимающих значения в множестве, состоящем из двух элементов 1 - 0. ^г , •т т иэ

Применение "ере^ду^ высказываний служит для выражения общности и позволяв формулировать законы алгебры логики дл,

любых высказываний данного вида.

Из одного или не^д^их высказываний или предикатов мож­но образовать новые высказывания или предикаты. Объединение простых высказываний „ сложные производится без учета смысла этих высказывании (предикатов) на основе определенных логиче­ских правил ("перац^ф^ц^

Число простейшие ^ических функций в конкретной алгебре логики зависит от код^ц^а значений истинности л:

(2.12)

Для двузначной булевой алгебры логики N определяется чис-

яом возможных двоичных наборов (п = 2): N = 16 . При п = 3 мож­но образовать N = 25<, логических функций.

Функции бинарной ^.^^ логики приведены в табл. 2.6, в которой собраны фор„у ^дси „ наименования функций, встре­чающиеся в различна литературных источниках.

Кроме логически^ функций, в логике предикатов имеются еще операции квантификдц^д _ кванторы. Это специальные операции, которые служат для выражения общности суждений и связанных с ними понятии 0-аол. ^ ^ позволяют на формальном языке исчис­ления предикатов го<^ ^ об од^ объекте, а о целом классе объектов.

Полную систему Логических функций называют логическим бази­сом. Для того, чтоб(,, система функций представляла собой базис, она должна обладать определенными свойствами.

частности^чт ы сц„^д функций была полной, необходимо и достаточно, тообы она содержала хот, ^ функцию: не сохраняющую константу единица. не сохраняющую константу ^ виненную. немонотонную несамодвойственную.

^ Полный логический базис содержит избыточное число функ­ции. 1 акая система <()у^ццй может остаться базисом при удалении из нее некоторых функций. Удаление функций можно производить до тех пор, пока сис-ге^ „g станет такой, что удалении из нее хотя бы одной из функци^ ^ образующих, будет приводить к невыпол­нению перечисленные требований к базису. Такую систему назы­вают минимальным бод .

112

Минимальными базисами бинарной алгебры логики являются базисы, включающие только две ф-нкции {-i, u} {-,, г^}. Функция отрицания не сохраняет константь ноль и единицу и не является монотонной, функции дизъюнкции u и конъюнкции п обеспечи­вают нелинейность не являются са\одвойственными (в силу при­веденных в табл. 2.8 теорем де-Мор-ана).

Таблица 2.7

Обозначения	Названия	Смысл
(Va)t (За)* (Б! а) и	Квантор общности Квантор существовании Квантор единственносп	Для любого а будет Ь Есть хотя бы одно а такое. что будет Ь Есть только одно а такое. что будет Ь

В этой связи существуют поня-ия дизъюнктивно-нормальной и коныонктивно-нормальной формы, “сегда удовлетворяющие требо­ваниям базиса.

В условиях выполнения требовжий к базису в алгебре логики доказывают теоремы, демонстрирующие свойства операций над высказываниями. Применяя эти теоремы, формально можно полу­чить правильный результат, не внжая в смысл проводимых иссле­дований. Примеры этих теорем или логических законов приведены в табл. 2.8.

Таблица 2. ft

Название свойства (закона), формулировка	Символическая запись
Замкнутость. Множество R содержит дизъюнкцию и конъюнкцию всех входящих в него элементов	a ub e R arib e R
Коммутативность Изменение последовательности элементов не изменяет значения дизъюнкции и конъюнкции	а иЬ =& иа a /~ib = Ь i~\a
•Ассоциативность Группировка внутри конъюнкции и дизъюнкции не меняет их значений	(a i~i /)) п с = а /-) (Ь п с) (а и Ь)ис = а и {Ь ис)
Дистрибутивность Прибавление элемента к произведению равносильно прибавлению этого элемента к сомножителям; умно­жение суммы на элемент равносильно умножению ^згаемых на этот элемент	a u(bDc)={aub) п(аис) a n(buc)= (anb) и (апс)
Чоемпотентность (закон технологии) Повторение элемента (прибавление или умножение) не ^ЙМеняет истинности элемента	а <--' a = a a ri a = а
Совместимость	а с/и = Ь в том и только в том случае, если а 1^1 b = Ь

Продолжение таблицы 2. И

Название свойства (закона). формулировка	Символическая запись
Дополнительность Для каждою элемента а множества R существует дополнение -i а или R - а	Частный случаГГ^ аи-, а= R -i/?=0 а'п-,а=0 -. 0 = R
Законы поглощения (абсорбции) Дизъюнкция произведения и одного нч ее членов экви­валентна этому члену. Конъюнкция суммы и одного из ее членов эквивалентна этому члену	а и (а 1^1 h) s a а п (а и h)s a
Законы двойственности (теоремы А. де-Моргана) Дополнение к пересечению а и h эквивалентно объ­единению их дополнении. Дополнение к объединению элементов (множеств) равно пересечению их дополнений
	а пЬ s а ^ Ь
	а и Ь s а г\ Ь
Инволюция (закон удвоенного отрицания}	-.(-i а) = а
Законы противоположности Если элемент а эквивалентен дополнению элемента Ь, то элемент Ь эквивалентен дополнению элемента а	a=b => b= a
Множество содержит элементы R = 1 и 0 = 0 такие, что для всякого элемента	а (-/0 = a a ^R = R anR= R ап0= а
Умножение одного пз элементов на дополнение вто­рого элемента не меняет дизъюнкции элементов	а *(-,*)=<”+/) а п (-i Ь) а а и h

Из элементарных функций алгебры логики формируют последо­вательности действий, отображающие процессы в системе от входа до выхода, т. е. логические алгоритмы.

На рис. 2.7 и 2.8 проиллюстрирована разная запись одного и то­го же алгоритма (соответствие обозначений рис. 2.7 и 2.8 приведено на рис. 2.9).

Этот же алгоритм может бытгь вписан следующим образом:

У\ =х,/{[(х^г\\\2)^х^хз];

(2.13 У1 = Х4 ^{[(Xlfl-^l)^,^^}.

(2.13)

Существует много форм запжси логических алгоритмов: в виде функций алгебры логики (2.13), в форие таблиц или матриц, "ма­шин Тьюринга", логических схюм по А.А.Ляпунову, с помощью рекурсивных функций, на языке? нормальных алгоритмов А.А.Ма­ркова, в виде программ для вьнчислительных машин на одном из языков программирования, в фсормс диаграмм Насси-Шнайдерма-на. С основными способами представления алгоритмов можно по­знакомиться в [2.27, 2.39, 2.65 и д1р.].

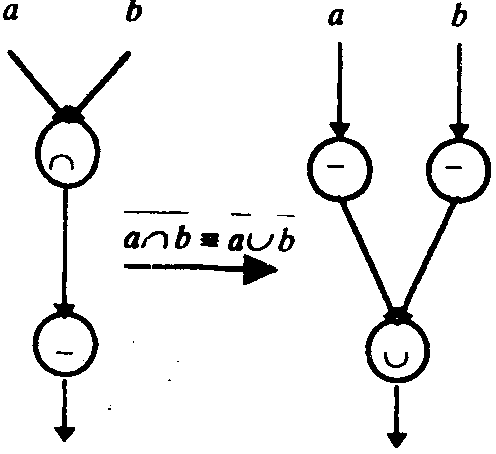
Логические алгоритмы могут! преобразовываться с использова­нием логических законов. Пример Применения одного из законов (теоремы А. де-Моргана) приведен tia рис. 2.10.

На базе логических пред­ставлений возникли и разви­ваются теории логического ана­лиза и логического синтеза. Эти теории основаны на при­менении средств алгебры ло­гики к задачам анализа и син­теза структур исследуемых си­стем, а также к задачам при­нятия решений в сложных проблемных ситуациях, воз-Рис. 2.10 никающих в системах или при

взаимодействии систем.

Задача логического анализа состоит в описании поведения сис­темы с известной структурой наборов системно-логических уравне­нии (функций алгебры логики - ФАЛ) и исследования полученно­го логического выражения с целью его минимизации, т. е. выясне­ния, нельзя ли получить более простую структуру (схему), содер­жащую меньшее число элементов (состояний), но осуществляющую

115

требуемые преобразования. Такие задачи возникают, например при создании автоматических систем контроля неисправностей, систем автоматического резервирования, обеспечения надежности и т. д.

Задача логического синтеза заключается в том, чтобы по из. вестному поведению системы определить ее структуру (в случаях, если она неизвестна или не полностью известна), т. е. сопоставить системе некоторый "автомат" - "черный ящик" с известными вход. ными и выходными воздействиями.

Таким образом, при логическом анализе задача сводится к ми­нимизации ФАЛ, т. е. к оптимизации в некотором смысле логиче­ского алгоритма. Задача логичского синтеза сложнее, она обычно решается путем последовательных приближений, и на промежуточ­ных этапах здесь также может быть полезна минимизация ФАЛ.

Минимизация осуществляется путем применения законов алге­бры логики, приведенных в табл. 2.8. Наиболее известными мето­дами минимизации ФАЛ являются: метод минимизирующих карт или таблиц (конъюнктивных или дизъюнктивных, импликатных); метод неопределенных коэффициентов; геометрические методы, метод Блека - Порецкого (с обзором методов минимизации ФАЛ можно познакомиться в [2.39], где даны ссылки на соответствующие перво­источники).

При возрастании числа переменных для минимизации ФАЛ применяют ЭВМ При этом логический алгоритм нужно перевести на один из языков программирова­ния, или при логическом анализе сложных ситуаций - разрабатывают промежуточ­ные языки проектирования или моделирования процессов управления (например, язык БИТ Э.Ф.Скороходько'. логический язык представления алгоритмов синтиа ЛЯПАС А.Д.Закревского² и др.).

Специфические особенности задачи логического синтеза при описании системы логическим автоматом вызвали возникновение и развитие самостоятельной научной дисциплины - теории автома­тов.

Логические методы представления систем возникли как детерминистские, но“ дальнейшем стали предприниматься попытки их расширения в сторону вероятной ных оценок.

Логические представления сыграли большую роль в развитии теоретической основы алгоритмизации и программирования. В ча­

стности, они лежат в основе теории алгорифмов (в дальнейшем -алгоритмов) А-А.Маркова.

Логические представления применяют в случаях исследований новых структур систем разной природы (технических объектов, текстов и др.), в которых характер взаимодействия между элемен­тами еще не настолько ясен, чтобы возможно было их представле­ние аналитическими методами, а статистические исследования либо затруднены, либо не привели к выявлению устойчивых закономер­ностей.

В то же время следует иметь в виду, что с помощью логических алгоритмов можно описывать не любые отношения, а лишь те, ко­торые предусмотрены законами алгебры логики.

В настоящее время логические представления широко применя­ются при исследовании и разработке автоматов разного рода, авто­матических систем контроля, при решении задач распознавания образов. На их основе развивается самостоятельный раздел теории формальных языков моделирования проблемных ситуаций и текстов.

В то же время смысловыражающие возможности логических методов ограничены базисом и не всегда позволяют адекватно от­образить реальную проблемную ситуацию. Поэтому стали пред­приниматься попытки создания вначале тернарной логики [1.30], а затем - и логик, в которых переменная может принимать не только крайние значения "истинно" - "ложно", но и какие-либо из проме­жуточных - многозначных логик [2.52], вплоть до непрерывной.

Однако отметим; что даже для тернарной логики В.Т.Кулику (1.30] так и не уда­лось создать непротиворечивый логический базис, н он обратился к созданию ин­формационных языков моделирования на основе лингвистических представлений.

Неудача попыток создания многозначных логик объяснима, если учесть, что вся математика, в т. ч. математическая логика для того, чтобы соответствовать принци­пам строго формальной дедуктивной системы (с учетом, конечно, теоремы ГЕделя), базируется на законе искяючечнога третьего (т. с. на предположении, что всякое событие, положение может быть истинным или ложным, третьего не дано).

Реальная же действительность не подчиняется этому закону, и поэтому для се моделирования необходимо либо создание подходов, основанных на формализации диалектической логики (специальное направление информационного моделирова­ния. развивающееся на этой основе, рассматривается в гл. 3), либо использование лингвистических и семиотических представлений, которые свободны от требования выполнения закона исключенного третьего, что и является иногда основанием для того, чтобы не включать эти направления в математику.

Лингвистические, семиотические яредстая-л е н и я. Математическая лингвистика и семиотика - самые "молодые" методы формализованного отображения систем. Вклю­чение их в разряд математических нельзя считать общеприз­нанным.

Некоторые исследователи (например. Ю.А.трейдер [1.58] считают, что лингви-стнк.1 в силу специфических особенностей, позволяющих моделировать развива-

117

ющиеся системы и процессы (то обеспстив”<т“от^вц^ закона исключенного третьего), не является математикой в сложи”™”" внимании этого термина. В то же время французская шхола математике!” (2.54 с^^ математическую лингви. стику разделом современной математики.

Математическая лингвистика возниц дд второй половине прошлого столетия как средство ф^ч^зованного изучения есте­ственных языков и вначале развивалась к^ алгебраическая лингви­стика. Первые полезные результаты алг^раической лингвистики связаны со структуралистским (дескрипт^цу,^ подходом. Одна­ко в силу отсутствия в тот период конце^дд развития языка эти работы привели к еще большему тупику g попытках построения универсальной грамматики, и был период ^эд.да структурализм считался неперспективным направлением ^вития науки о языке и даже был гоним.

Активное возрождение математическое лингвистики началось в 50 - 60-е гг. и связано в значительной степ^д р потребностями при­кладных технических дисциплин, У^^ч^вшисся задачи которых перестали удовлетворять методы классиче^дд математики, а в ряде случаев - и формальной математической л^гнк^

В период уменьшения интереса к матсйстя“”о( лингвистике появилось ста­тистическое направление, которое называв "п°\ст^ст6 ммгмстжой или лингвистической статистикой^.9. 8.29,8.30 и др.}.

Семиотика возникла как наука о зн^дд. знаковых системах. Однако некоторые школы, развивавшие семиотические представле­ния, настолько равноправно пользу¹⁰¹!'⁰¹ g семиотике понятиями математической лингвистики, такими, ка^ тезаурус, грамматика. семантика и т. п. (характеризуемыми ниж^ „g выделяя при этом в отдельное направление лингвосемио1"ику (\^ у^ делает, например, Ю.С.Степанов [2.44]), что часто трудно определить, к какой облас^ ти относится модель - математической лин^уд^д ,цщ семиотике.

В то же время именно в лингво^емиоп^^ достигнуты наиболее конструктивные результаты, которое мог^ gy^ полезны при ис­следовании систем различной физической природы, а другие при­менения семиотики как науки о знаках нос^ g большей мере харак­тер методологического средства ддя пояс^ддд результатов, кото­рые ранее были получены в геометрии, a^pg д других разделах математики.

Поэтому мы решили для целей "Решения математической лингвистики и семиотики к системным Ицледованиям рассматри­вать эти направления совместно, не ^^^Р^дая особо, что фактиче­ски речь пойдет о яингвосемиотике.

Основными понятиями, на которых баз^ру^^д лингвистические представления, являются понятия: 1иезауР\,с грамматика, семанти­ка, прагматика. 118

Термин тезаурус (от греч. "вт|6аироС', "thesauroe" - сокровищ­ница, богатство, клад, запас и т. п.) в общем случае характеризует "совокупность научных знаний о явлениях и законах внешнего мира д духовной деятельности людей, накопленную всем человеческим обществом" [8.21]. Этот термин был введен в современную литера-•дгру по языкознанию и информатике в 1956 году Кембриджской группой по изучению языков. В то же время термин существовал раньше: в эпоху Возрождения тезаурусами называли энциклопедии. С обзором определений тезауруса можно познакомиться в [8.22].

В математической лингвистике и семиотике термин тезаурус ис­пользуется в более узком смысле, для характеристики конкретного языка, его многоуровневой структуры. Для этих целей удобно поль­зоваться одним из принятых в лингвистике определений тезауруса как "множества смысловыражающих элементов цзыка с заданными смысловыми отношениями." [2.63].

Это определение позволяет представить структуру языка в виде уровней (страт) множеств (например, слов, словосочетаний, пред­ложений, абзацев и т. п.), смысловыражающие элементы каждого из которых формиру­

ются из смысловы­ражающих элемен­тов предшествую­щих структурных уровней (см. рис. 2.11).

Правила (G/, G2) формирова­ния смысловыража­ющих элементов второго и третьего уровней в тезаурус не входят, в тезау­русе определяется только вид и наи­менование уровня, характер и вид с^Ысловырахающих элементов.

Иногда вместо термина смысловы­ражающие элемен­ты используется термин синтаксические единицы тезауруса. На наш взгляд, это менее удачный термин, так как при формировании эле­ментов нового множества смысловыражающих элементов каждого последующего уровня (при образовании слов из букв, фраз и пред-119

ложений из слов) у элементов вновь образованного множества по. является новый смысл, т. е. как бы проявляется закономерность целостности, и это хорошо отражает термин "смысловыражающи,, элемент".

В таком толковании понятие тезауруса можно конструктивно использовать при создании искусственных языков - языков модели. рования, автоматизации проектирования, информационно-поиско­вых языков. Оно позволяет охарактеризовать язык с точки зрения уровней обобщения, ввести правила их использования при индекси­ровании информации.

Можно говорить о глубине тезауруса того или иного языка, ха­рактеризуемой числом уровней, о видах уровней обобщения, и, поль­зуясь этими понятиями, сравнивать языки, выбирать более подхо­дящий для рассматриваемой задачи или, охарактеризовав структуру языка, организовать процесс его разработки.

Под грамматикой (которую иногда называют синтактикой, синтаксисом, что сужает понятие грамматики, исключая из него морфологию) понимаются правила, с помощью которых формиру­ются смысловыражающие элементы языка (на рис. 2.11 два вида правил - G1 и G2, которые иногда называют грамматиками 1-го и 2-го рода). Пользуясь этими правилами, можно "порождать" (формировать) грамматически (синтаксически) правильные кон­струкции или распознавать их грамматическую правильность.

Термин грамматика употребляется в лингвистике и как укоро­ченная замена термина "формальная грамматика", который имеет иной смысл и будет охарактеризован ниже.

Под семантикой понимается содержание, значение, смысл формируемых или распознаваемых конструкций языка;

под прагматикой - полезность для данной цели, задачи.

В естественном языке различить понятия, с помощью которых характеризуются термины семантика я прагматика, трудно; обыч­но пояснить различие можно лишь при парном сопоставлении тер­минов:

<сема(ггика> :: = <содержание> | <смысл> | <значение>;

<прагматика> : := <смысл> | <значение> | <полезность>.

Поэтому принято рассматривать эти понятия на примерах. Поясним различие между семантически и прагматически правильными конструкциями языка на сле­дующих легко запоминающихся примерах.

Традиционно для пояснения синтаксической правильности и семантической бес­смыслицы используется предложенный Л.В.Щербой пример "Глокая куздра тщегМ борзданула бокра и курдычет бокренка" (в котором просто нет ни одного слова есте­ственного языка, имеющего смысл). Но примеры можно найти и в естественной речи.

Предложение "Муха лукаво всплеснула зубами" синтаксически правильное, но не имеет смысла в естественном русском языке в обиходном, широком употреблении.

120

естся с точки зрения пользователей русским языком семантически непра-т. <; "_ (исключим пока гипотетическую ситуацию сказки, в которой муха может ^в№яь „адспена указанными свойствами). ⁶ Поугос предложение "Маленькая девочка собирает цсеты на лугу' - синтаксичс-

сема1ггически правильное. Однако для директора завода (если зто луг. а не ^1;1(и ской газон, и - учтем личный фактор - если эта девочка не его дочь) это пред-^WHC не несет никакой информации, т. е. прагматически (с точки зрения целей оводап-сля) является неправильным. Другое дело, если "Ияанов (который в данный ечт должен находиться на рабочем месте) собирает цветы на .ч)'гу". Тогда что ^^дпожение было бы и прагматически правильным.

" Зозвратимся теперь к примеру с мухой. Приведенное предложение, семантиче-

^правильное. может в гипотетической ситуации сказки оказаться прагматически ''тавияьным. что важно иметь в виду при применении лингвистических представле­ний

При создании и использовании искусственных языков применя­ют такие понятия структурной лингвистики, как порождающая и распознающая грамматика.

Под порождающей грамматикой понимается совокупность пра­вил, с помощью которых обеспечивается возможность формирова­ния (порождения) из первичных элементов (словаря) синтаксически правильных конструкций. Под распознающей грамматикой - прави­ла, с помощью которых обеспечивается возможность распознава­ния синтаксической правильности предложений, фраз или других фрагментов языка.

Все рассмотренные понятия в равной мере используются как в математической лингвистике, так и в лингвистической семиотике. Некоторую условную границу между ними можно провести, лишь введя понятие классы формальных грамматик (как теорий матема­тической лингвистики).

На базе лингвистических представлений развивается теория формальных грамматик Н-Хомского [2.56, 2.57 и др.]. Классы фор­мальных грамматик Н.Хомского считаются основой теории фор­мальных языков.

Формальный язык определяют как множество (конечное или бес­конечное) предложений (или "цепочек"), каждое из которых имеет конечную длину и построено с помощью некоторых операций (правил) из конечного множества элементов (символов), составляющих алфа­вит языка.

Формальную грамматику определяют в виде четверки множеств:

С=<^^,/г.Д>, (2.14)

где vt - множество основных или терминальных символов; Уц -множество вспомогательных или нетерминальных символов; R -множество правил вывода, или продукций, которые могут иметь вид:

а-^Р, (2.15) '•Де Ве(^^),

171

т. е. р - цепочка конечной длины из терминальных и нетерминал), ных символов множеств Ут и V^,

а а е (У-г и V„) V^ vt ^ У Л (2.16)

т. е. а является цепочкой из терминальных и нетерминальных сиц. волов, содержащей по крайней мере один нетерминальный символ из Уц; А - множество аксиом (в грамматиках комбинаторного ти. па, к которым относятся грамматики Н.Хомского, А состоит из одного начального символа S, причем S с Уц.

Учитывая, тго в литературе по формальным грамматикам, как правило, не стго. мятся к содержательной интерпретации получаемых выводов, а рассматривают лщщ формальную сторону процессов порождения и распознавания принадлежности цепочек к соответствующему классу грамматик, приведем содержательный прима порождающей грамматики. Предположим, дано:

vt= <ei, вг.л.л > Vц=<S, P>

Порождающая грамматика Распознающая грамматика S-^SP (I) SP-^S (1) 5-T”eiS(2) eiS-^S(2') (2.17) R= {S-^azS (3) aiS-^S (3) S->n (4) л->5(4') Р->л (5) л->Р{5)

Применяя правила К левой части (2.17) в приведенной последовательности, по­лучим:

SssS P =>ei SP=>eie^SP^emnP=^eieinA (1) (2) (3) (4) (5)

Это - формальная сторона процесса порождения. Для того, чтобы получить ин­терпретируемое выражение, нужно расшифровать терминальные символы, вклюяен-ные в Уц. где ei - "все", вз -"возрасты", п - "покорны", л - "любви".

Тогда полученное предложение "ei вз я л" - "все возрасты покорны любви". Если изменить последовательность применения правил, то будут получаться Дру­гие предложения. Например, если применить правила в последовательности (1) -^? (3) =^ (2) => (4) => (5), то получится "возрасты все покорны любви'. Если применил” не все правила: например. (I) =>(!) =>(4) ^(5), то получим "все покорны любви".

Если же попытаться получить предложение, как у Л.С.Пушкина - "Любви W возрасты покорны", то. как бы мы не меняли последовательность правил, получи¹¹ эту фразу не удается. Нужно изменить первое правило: вместо S -” SP включить в R правило S -” PS.

Из примера видно, что вид порождаемых цепочек (предложе­ний) зависит от вида правил (исчисления) и от последовательности ^ применения (алгоритма).

С помощью приведенного примера легко также продемонстри­ровать тесную связь понятия "грамматически правильный" с, языком (грамматикой). 122

„знающая грамматика для рассматриваемого примера будет содержать как •• еоевернутые" правила - правая часть (2.17). которые должны применяться в б" _' последовательности. Пример представления анализа правильности пред-^Р³ ^ (; помощью правил распознающей грамматики приведен на рис. 2.12.

•^10ЖС При распознавании правильности предложения если не оговаривать, что предложение (цепочка) грамматиче­ски правильно с точки зрения правил данного формального языка, то мож­но, пользуясь формальной граммати­кой в первоначальном виде, получить вывод, что приведенная фраза Пуш­кина грамматически неправильна с точки зрения правил грамматики (2.18).

Действительно, с точки зрения пра­вил грамматики для построения дело­вого текста, которым соответствуют правила (2.18). другие поэтические строки часто получали бы формаль­ную оценку "грамматически непра­вильно". И, напротив, если бы мы

построили грамматику на основе анализа пушкинского стиля, то в деловом тексте

получили бы предложения типа "Я решение свое принял правильное" (подобно фразе

'Я памятник себе воздвиг нерукотворный").

Сказанное позволяет легко представить полезность определе­ния формальной грамматики при создании языка моделирования соответствующего литературного или музыкального произведения

- пародий, подражательств или, как иногда принято говорить, про­изведений соответствующего стиля или класса (например, известны работы Р.Х.Зарипова по моделированию музыкальных произведе­ний в стиле, или в классе, массовых советских песен, моделирование процесса сочинения стихотворных произведений и т. п.' ).

Подобным же образом можно моделировать порождение дело­вых писем или других документов, имеющих, как правило, не толь­ко формализованный стиль, но и формальную структуру.

Аналогично можно создавать языки моделирования структур, языки автоматизации проектирования сложных устройств и систем определенного вида (класса).

Основу подобных работ составляют идеи, которые можно пояс-чить с помощью классов грамматик, впервые предложенных Н-Хомским [2.56, 2.57].

Разделение грамматик на классы определяется видом правил вы-^Да R. В зависимости от правил R можно выделить четыре основ-^ны^ наиболее часто рассматриваемых класса грамматик (в полной ^рии формальных грамматик с правилами типа подстановки есть ^и "Ромежуточные классы):

I.„класс На правила вывода накладывается только одно требование, чтобы, левой части правила вывода было t^"⁷” ^ww\lule символов, чем в правой, т. е. ^ правила были нсукорачивающим”¹¹,¹" У^чъшали число символов в выводимы, цепочках Этот класс грамматик “⁰⁶"⁴"⁰ -"к и называют неутрачивающими (цу, грамматиками). Иногда их также зазывают грамматиками типа ноль (нулевого типа)

пни алгоритмическими.

-•-и класс На правила вывода. ГП^чмо требований неукорачиваемоста. наклады. вается ограничение, чтобы на к^”^⁰" ^шаге "'менялся только один символ в вд„. тексте, т е. чтобы Z1 В Z2 -”Z/ ^ ^z2- ^{где в} - ^отн нетерминальный символ, к/. непустая цепочка символов, т. с. ^w * ⁰ Грамматику такого вида называют ^ текстной. контекстно-связанной *”^и ^1шогда применяют термин - грамматика wu, средственнь^ составляющих (//с-грамматики)

3-й класс. Если. кроме нсукораЧ¹"”³⁶”⁰"¹¹ требуется, чтобы правила имени вид fi -* В (т. е. а всегда состоит из оЛ^⁰ в"'"могательного символа), то грамматик, такого типа называют бесконтексУ"¹⁰" ^или контекстно-свободной (А-С-грамматиха).

+i! класс Если на правила вы^⁰^^ накладывается по сравнению с третьим клад. сом еще одно ограничение, трсбу”^"^ ^етобы ч "Равилах вывода нетерминальна символ всегда стоял справа или с?*.*”"- т. е. с одной стороны, то грамматику „азы. вают автоматной (/”-грамматике””) ^Екш нетерминальный символ стоит слева, т. е. правила имеют вид А -” ай или ^А -* ^а' ^[де <-⁴- ^ ^€ ^ ^{а €} ^г. автоматная грам. матика является праюлинейной-. -^ехяи нетерминальный символ стоит справа - то автоматную грамматику называю-^ леволинечнои.

В теории формальных грв""'"™ показывается, что имеет место

следующее соотношение:

Л £ КСс ЯСс НУ. (2.18)

Иногда доказывают, ч-Г^{43 имеет мест0} строгое вхождение:

^ с: КС с: НС с НУ. (2.18а)

При исследовании раз”¹"^{31 классов} формальных грамматик по­лучены результаты, котор^® позволяют сделать вывод, что по ме. ре уменьшения числа огра^м^ний, накладываемых на правила вы­вода, т е. по мере продви^ии" ^в (²-¹⁸) ^слева направо, в языке уве­личивается возможность отображение смысла (повышается смыс-ловыражающая способность языка, т. е. возможность выражения с помощью формальных np³"¹" семантических особенностей про­блемной ситуации): говор^- ^что формальная система становитй более богатой. Однако пр** ^это" ^{в языке} ра"^ тасло алгоритми­чески неразрешимых про^™"' ^т- ^е- увеличивается число положе­ний, истинность или ложн*^¹' которых не может быть доказана”

рамках формальной систе”*""³"^- . Здесь мы сталкиваемся фактически с геделевской проблемой

[2 48] которая в теории форизль”^ языков обсуждается обычно” терминах этой теории. А ”*менно: вводится понятие "операция МУ делена (или не определена) w множестве языков данного класса ; ” считают, что операция оПР^^”" н³ множестве языков данного класса, если после применяй" ее к языкам, входящим в это множе­ство, получается язык, пр^^ежащнй множеству языков этого

124

Например, если Я, с; КС и Я, с КС, и если (Я, иЯ,) с КС, то ^кл яция объединения (^определена на классе /СС-языков. ⁰⁽¹ Характеризуя с помощью введенного понятия классы языков,

чечают, что в последовательности (2.18) по мере продвижения ^от ва направо увеличивается число операций, которые не определе-^сл на множестве языков данного класса.

Чяесь, правда, следует оговорить, что дело обстоит не так прямолинейно. Точнее дц сказать, что для большого числа операций нет доказательств, что они ппеяслсны не классах ЯС-языков и ЯУ-язьпсов, т. с. от-и доказательства становятся "ее или вообще (в силу теоремы Гёделя) нереализуемы средствами теории фор-дадьны! грамматик.

В упрощенном виде мы представили проблему для того, чтобы обратить внимание тех, кто будет заниматься разработкой языков программирования или программных систем, языков моделирова­ния, автоматизации проектирования, на необходимость учитывать закономерность: чем большими смысловыражающими возможно­стями обладает знаковая система, тем в большей мере растет в ней число алгоритмически неразрешимых проблем (т. е. тем менее доказа­тельны в ней формальные процедуры).

При выходе в класс произвольных грамматик, в котором не выполняется даже условие исукорачивасмости. доказать допустимость тех или иных формальных пре­образований средствами математической лингвистики практически невозможно, и поэтому в поисках новых средств исследователи обратились к семиотическим пред­ставлениям. Здесь можно провести как бы формальную границу между лингвистикой и семиотикой-

Семиотические представления пользуются другими по сравнению с математической лингвистикой средствами исследования семанти­ческих возможностей языков. В частности, понятием треугольника Фреге [2.27, 2.62 и др.], согласно которому любой знак имеет форму. синтаксис (означаемое знака) и семантику (смысл, значение).

Такая исходная терминология позволяет отойти от представле­ний формальных грамматик Н.Хомского, имеющих отношения типа подстановки, и конструировать грамматику, используя более широкий спектр отношений.

В частности, на границе лингвистики и семиотики возникли язы­ки синтагматического типа, т. е. языки, использующие правила тапа (a, ric fry}, называемые синтагмой, где о, е А. Ъ^ е В - взаимо­действующие множества (подклассы) исходных понятий языка;

^е R - множество отношений, которые могут иметь произвольный '"Д. Однако такая свобода, как уже отмечалось выше, приводит к увеличению числа антиномий в языке.

Например, для информационно-поискового языка это означает ухудшение его "ОДеств (в частности - релевантности, т. е. соответствия выдачи запросу пользоватс-^л*) в силу того, что при реализация поискового алгоритма могут возникнуть замк-"У^е циклы, обусловленные противоречивыми правилами грамматики языка.

125

Поэтому используемые отношения все же пытаются конкрети­зировать.

В частности, Ю.А.Шрейдер [2.61] исследовал возможности ис­пользования отношений эквивалентности, толерантности и стро. гого порядка, определяемых на основе свойств рефлексивности, сим. метртности и транзитивности (табл. 2.9).

Таблица 2.9

Отношение	Свойство
	Рефлексивность	Симметричность	Транзитивность
Эквивалентность Толерантность Строгий порядок	+ +	+ +	+ +

С примерами применения этих отношений для отображения фраз и текстов естественного языка можно познакомиться в (2.61, 2.62]. Но для пояснения возможностей, появляющихся при таком подходе к созданию языка проиллюстрируем применение отноше­ния толерантности.

Как видно из таблицы, по определению толерантность - осо­бый вид сходства, при котором сопоставляемые элементы языка находятся в отношении, обладающем рефлексивностью и симмет­ричностью, но не обладающем транзитивностью. Это означает, что, например, если при сопоставлении слов ввести допустимую ошибку в один символ, то отношение сходства между первым и вторым словами могут быть признаны (с точностью до допусти­мой ошибки) рефлексивным и симметричным; аналогично - между вторым и третьим; но первое и третье слова уже могут отличаться не одним, а двумя символами, и сходство между ними можно во­обще не обнаружить, т. е. не будет выполнено отношение транзи­тивности.

В [2.61] приводится образный пример, как в результате применения такого от­ношения можно получить из "мухи" "слона" (т. е. из слова "муха" получить слово "слов"), а также иллюстрация понятия транзитивности с помощью гравюры гол­ландского художника М.К.Эсхсра "Небо и вода" (на которой едва различимые пре­образования на каждом шаге сверху вниз постепенно превращают контуры птиц в контуры рыб).

Возникновение подобных ситуаций важно учитывать при раз­работке языков для формального кодирования передачи текстов и восстановления их в месте приема.

С помощью отношения толерантности можно отобразить неко­торые отношения между словами естественного языка.

Например: рам-а т стол (2.19)

стол t книг-у , где т - операция установления сходства. 126

Приведенные соотношения (2.19) означают, что в синтагме "рама ^х стол" имеет место отношение сходства с точностью до рефлексии и симметрии, в синтагме "стол т книгу" - тоже. а между элементами синтагмы "рам-а" - "книг-у" сходства нет в силу невы­полнения по определению для рассматриваемого отношения свой­ства транзитивности.

Попытаемся интерпретировать формальную запись (2.19). Со­держательный анализ этих соотношений позволяет понять, что в них отражено сходство по падежу: слова мужского рода ("стол") могут употребляться в русском языке в одинаковой форме в име­нительном (первая строка) и винительном (вторая строка) падеже, в то время, как слова женского рода имеют в этих падежах разную форму, что и обусловило нетранзитивность.

Аналогично можно отобразить сходство по роду. так как в русском языке могут использоваться одни и те же имена для женщин и мужчин, что в тексте без дополни­тельных пояснений или учета формы глагола может оказаться нераспознаваемым. Можно также отразить понятие места в предложении или места предложения в абзаце и т. п.

Таким образом, вводя в язык отношение толерантности (напри­мер. путем формирования классов толерантности) можно отразить в языке взаимоотношения между словами и высказываниями более полно и точно, чем это позволяют делать отношения математи­ческой логики или грамматик Н.Хомского. Такие языки необходи­мы при расшифровке древних рукописей, при автоматизации про­цесса перевода с одного языка на другой.

Однако, следует иметь в виду, что создание подобных языков - весьма сложный н трудоемкий процесс, и поэтому в практике информационного поиска или разра­ботки языков моделирования в тех случаях, когда есть возможность отразить <х;о-бенности моделируемой ситуации иным способом, рассматриваемый подход не применяют.

В частности, при разработке некоторых информационно-поисковых языков было предложено вводить при индексировании текста понятия "указатели роли", "ука-чтсли связи", которые легче интерпретируются при ручном индексировании, чем п<>-итие толерантности. В то же время при автоматизации индексирования может воч-впЕнуть необходимость в использовании отношений, приведенных в табл. 2.9. по­скольку они. обладая большими по сравнению с лингвистическими представления­ми смысловыражающими возможностями, все же базируются на определенной фор­мальной основе, которая может позволить сделать язык более алгоритмизируемым.

Гр афические методы. Понятие графа первоначально было введено Л.Эйлером. Графические представления позволяют наглядно отображать структуры сложных систем и процессов, про-"сходящих в них. С этой точки зрения они могут рассматриваться ^к промежуточные между МФПС и МАИС. Действительно, такие средства, как графики, диаграммы, гистограммы, древовидные ^уктуры, можно отнести к средствам активизации интуиции спе-Чиалистов.

В то же время, есть и возникшие на основе графических предста. влений методы, которые позволяют ставить и решать вопросы on. тимизации процессов организации, управления, проектирования, к являются математическими методами в традиционном смысле. Та­ковы. в частности, геометрия, теория графов (основные понятия теории графов приведены в таблице 2.10. которая поможет начать самостоятельное изучение теории графов) и возникшие на основе последней прикладные теории - PERr. сетевого планирования ц управления {СПУ) [2.24, 2.25. 2.46 и др.], а позднее и ряд методов статистического сетевого .моделирования с использованием веро.

ятностных оценок графов.

Таблица 2.10

Понятие	Определение или опредаумщий прина”	Изображение
Гро<р(Г)	Множество элементов х, - х„ u	Источник ('Исток) Сто”' — -^^"^^"" i —^^^^в о^о^СР*.
	отношений и,- Un меэкЗу пики	"о '—вершина Дуга (рсоро)
Г. конечный м Х	Конечное множество	00 0-0 X. Хп
	мементор
		Un
Г. конечный no If	Конечное множество отношении	Хд s-— X
Г. немпраСтетом (неориентиробан-ныи)	Элементу не упорядочен” (направление отноше­нии не определено)	X. X.
Г. напраВмнныи (ориентирован -иьш)	Элементы упоридоченн . ('направление отношении определено)	0-—-0-"~*DC$0 х, x
Г. cunneinpu-ческии	Двухсторонние отношения	000° "о
Г. асимметри­ческий	Односторонние отношения	u-^cr'^o^'o л ”
		o°~"o <Г^о
Г несо/чныи	Обособленные части	х- х 0
Г.сбяэныи	Камдсч пара элементов сЧязана между собой непосредственно или через другие элементе	сГ^(Г~~'сГ~'а "0 x
Г. полней	Любая пара элементов соединена непосредст­венно хлтя оы одним	^^^
	^тиП1М/”*ч:9^ | * лу

Продолжение таблицы 2.10

^pb связи с большой распространенностью СПУ остановимся кра­тко на ее недостатках. Во-первых она первоначально была ори­ентирована на анализ только одного класса графов - направленных (не имеющих обратных связей, т. е. циклов, петель; такие требова­ния содержались в руководящих материалах по формированию сетевых планов предприятий), и это явилось одной из причин того, что впоследствии при применении сетевых методов для отображе­ния ситуаций, не подчиняющихся этим ограничениям, был исполь-^ван термин сетевое моделирование, снимающий требование одно­направленности графа. И, во-вторых, (что наиболее существенно) .-"ри формировании сетевых планов необходимо участие высококва­лифицированных специалистов, хорошо знающих процессы в сис-^ме (эту работу нельзя поручить техническим работникам, кото-Рые полезны лишь при оформлении сетевых графиков и обработке 129

результатов оценки. При этом по результатам кледованиия оказа лось, что доля "ручного" труда ЛПР при разработке сете-евого гра фика составляет по оценкам специалистов ддо55% ббчдиих затрат времени на анализ ситуаций и процессов с исдаользованиемк сетевого моделирования. Для снижения доли "ручного" труда полеезно соче. тать графические представления с лингвистивчвкими и сеемиотиче^ скими, разрабатывая языки автоматизации “формирован иия сетевой модели. На основе такого сочетания методов возникли вновые на­правления моделирования - структурно-ли "нгмстическоое, графо. семиотическое и т. п. Примеры разработки методик и яззыков мо­делирования, использующих подобные предстамения, буддут приве. дены в гл. 8.