Биномиальное распределение. Распределение Пуассона

Важным примером распределения дискретной случайной величины является биноминальное распределение. Пусть имеется некоторое случайное событие А, вероятность появления которого в каждом из испытаний постоянна и равна p. Производится n независимых испытаний. Случайная величина Х – число появлений события А в n независимых испытаниях. Возможными значениями с.в. Х, распределенной по биноминальному закону, являются все целые числа от 0 до n. Величина Вер{Х = k} – вероятность того, что в n испытаниях событие А произойдет ровно k раз – вычисляется по формуле Бернулли.

(21)

где q = 1 – р.

Введем в рассмотрение случайные величины Х_i, i = 1,2,… n-число появлений события А в i-испытании. Тогда Х = Х₁ + Х₂ + …+ Х_n – общее число появлений события А в n независимых испытаниях – равно сумме числа появления события А в каждом из n испытаний. Случайные величины Х_i, i = 1,2,…, n принимают только два значения: 0 – с вероятностью q и 1 – с вероятностью p.

Следовательно,

Далее,

(22)

а так как случайные величины X_i независимы, то

(23)

Таким образом, математическое ожидание числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события А, а дисперсия равна произведению числа испытаний на вероятность появления события А и на вероятность его не появления.

Найдем математическое ожидание и дисперсию случайной, имеющей распределение Пуассона:

M(X)= m = , D(X)= m² - = .

Пример19. Пусть некоторая случайная величина распределена по закону Пуассона. По результатам наблюдаемых значений 2; 1; 1; 3; 1; 4; 2; 5; 1; 7 оценить неизвестный параметр случайной величины.

Решение. Математическое ожидание M(X) случайной величины есть ее среднее значение. Для случайной величины, распределенной по закону Пуассона

Пример 20. Бросаются две игральные кости. Случайная величина Х – число очков, выпавших на первой игральной кости; Y – на второй; Z – суммарное число очков, выпавших на двух игральных костях. Вычислить математическое ожидание и дисперсию случайных величин Х, Y, Z.

Решение. Закон распределения с.в. Х задается таблицей:

Таблица 4

X	1	2	3	4	5	6
Р

Законы распределения с.в. X и Y совпадают, т.е. X = Y, а Z = X + Y. Заметим, что Z = X + Y  2·X (!!) .

Вычислим математическое ожидание и дисперсию с.в. Z, пользуясь законом распределения, заданным в таблице 1:

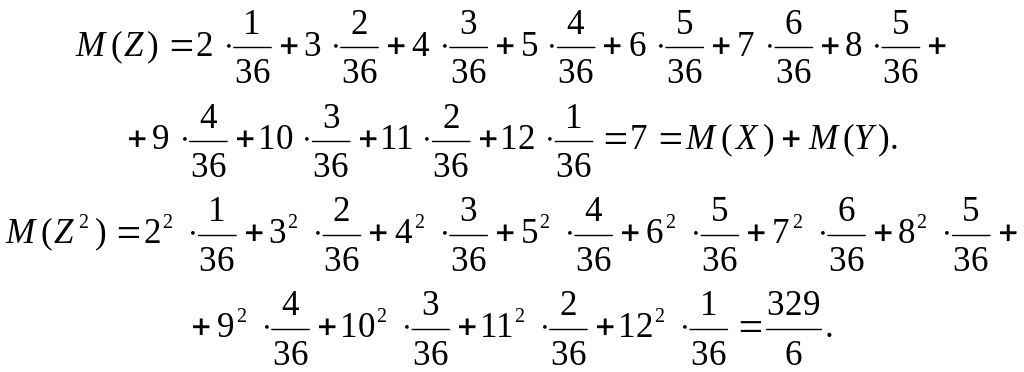
Пример 21. Из ящика, содержащего 3 черных и 5 белых шаров, наудачу извлекается 4 шара. Случайная величина Х – число вытащенных белых шаров. Найти математическое ожидание и дисперсию с.в. Х.

Решение. Построим закон распределения с.в. Х. Она может принимать любое значение от 1 до 4.

Таблица 5

X	1	2	3	4
P	p1	P2	р3	р4

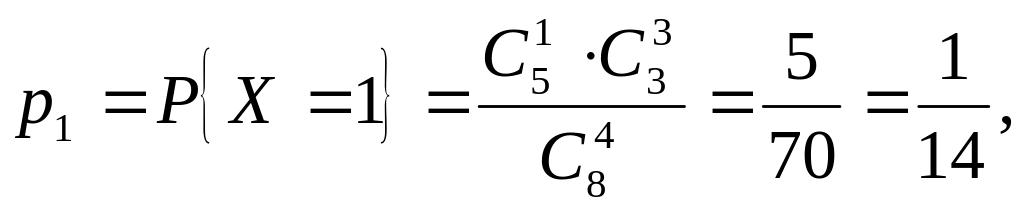
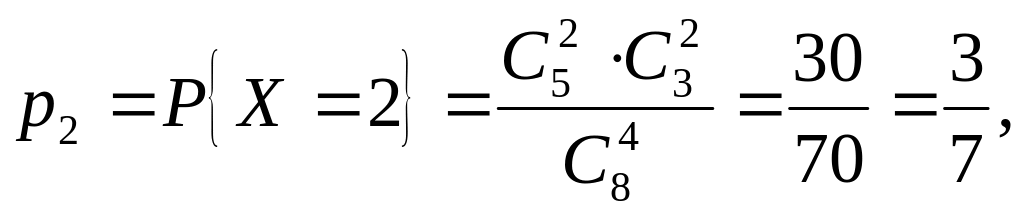
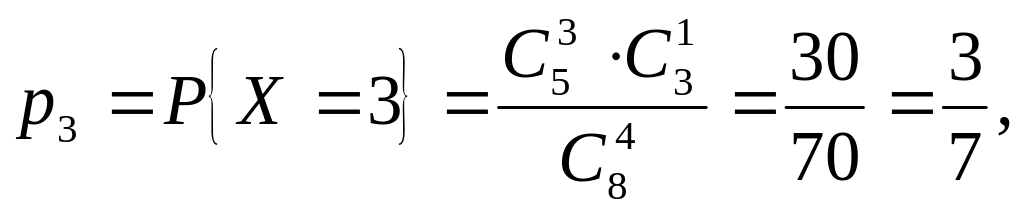
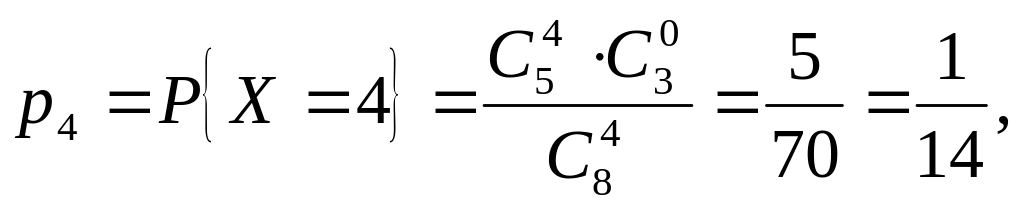
Для того, чтобы понять, что представляет собой сумма случайных величин, рассмотрим следующий пример.

Пример 22. Производится стрельба из трех орудий. Первое попадает при каждом выстреле с вероятностью 0.8, второе - 0.5, третье - 0.6. Все орудия выстрелили по одному разу. Случайная величина X - число снарядов, попавших в цель. Требуется построить закон распределения, найти математическое ожидание и дисперсию случайной величины X.

Решение. Введем обозначения: A - cобытие, заключающееся в том, что первое орудие попало в цель, B - второе орудие попало в цель, C - третье. Далее находим P(X=0)=P

P(X=1)=P

=

P(X=2)=P

=

P(X=3)=P

Закон распределения нашей случайной величины имеет вид:

X	0	1	2	3
P	0.04	0.26	0.46	0.24

Вычислим математическое ожидание и дисперсию:

M(X)=

D(X)=M( )- =

Введем в рассмотрение следующие случайные величины: X₁- число снарядов, попавших в цель из первого орудия, X₂ - число снарядов, попавших в цель из первого орудия,

X₃ - число снарядов, попавших в цель из первого орудия. Законы распределения этих случайных величин имеют вид:

X1	0	1		X2	0	1		X3	0	1
P	0.2	0.8		P	0.5	0.5		P	0.4	0.6

M(X₁)=

D(X₁)=M( )-M²(X₁)=

Аналогично находим M(X₂) = 0.5; M(X₃) = 0.6; D(X₂) = 0.25; D(X₃) = 0.24.

Нетрудно видеть, что X=X₁+X₂+X₃ , следовательно

М(X)= M(X₁)+ M(X₂)+ M(X₃)=0.8+0.5+0.6=1.9.

Так как случайные величины X₁, X₂, X₃ независимы, то

D(X)= D(X₁)+ D(X₂)+ D(X₃)=0.16+0.25+0.24=0.65.

Предположим, что из первого орудия выстрелили 100 раз, из второго -200, из третьего-250 раз, случайная величина X число попаданий в цель. Построить закон распределения такой случайной величины сложно, так как она может принимать очень много значений. возможные значения- любое число от 0 до 550. Однако M(X)= D(X)= среднее квадратичное отклонение Полученный результат можно интерпретировать следующим образом (приближенно)- в цель попадет 550 снарядов ‘плюс минус’ 11.