Случайные события

Теория вероятностей – это наука о закономерностях массовых случайных событий. Событие, которое при воспроизведении некоторого комплекса условий может произойти, а может и не произойти, называется случайным. Случайные события обозначаются большими буквами латинского алфавита (А, В, С и т.д.). Далее вместо слов «воспроизведен комплекс условий» будем писать «произведено испытание». Событие, которое всегда происходит при проведении испытания, называется достоверным и обозначается U; событие, которое никогда не происходит, называется невозможным и обозначается V.

Пусть имеется пара случайных событий А, В. Событие, заключающееся в появлении хотя бы одного из событий А или В, называется суммой и обозначается А+В (иногда А В), событие, заключающееся в совместном появлении событий А и В называется их произведением и обозначается А ·В (иногда А В).

Событие заключающееся в том, что событие А не произошло называется противоположным событием событию А и обозначается .

Говорят, что событие А влечет за собой событие В, если при появлении события А, обязательно происходит и событие В (обозначается А В).

Если А В и В А, то такие события называются равносильными: А=В.

Пример 1. Два стрелка выстрелили в цель по одному разу. Пусть событие А – попал первый стрелок; событие В – попал второй. Тогда

А+В – цель поражена (попал хотя бы один); А ·В – попали оба;

- первый промахнулся; · - никто не попал; (очевидно, ).

При умножении и сложении случайных событий можно поступать точно также, как и при сложении и умножении обычных чисел, только следует иметь в виду следующие формулы:

А ·А = А, А+А = А, А+U = U, А+V = А,

А ·U = А, А ·V = V, = А.

А +В = В +А, А ·В = В ·А,

А + (В + С) = (А + В) + С, А ·(В + С) = А ·В + А ·С.

События А и В называются несовместимыми (несовместными), если их совместное появление невозможно, т.е. А ·В = V.

Классическое определение вероятности

Говорят, что событие А подразделяется на m частных случаев А₁, А₂,…, А_m , если А =А₁ + А₂ +…+ А_m , т.е. А происходит тогда и только тогда, когда происходит одно из событий А_j, j 1 : m. Говорят, что события А₁, А₂,…А_n образуют полную группу, если А₁ + А₂ +…+ А_n = U, т.е. при проведении испытания обязательно происходит одно и только одно из событий А₁, А₂,…, А_n.

В самом общем случае определить вероятность случайного события непросто. Однако в простых случаях, когда число исходов испытания конечно, можно дать не только определение вероятности, но и способ ее вычисления.

Определение. Если событие А подразделяется на m частных случаев, входящих в полную группу, состоящую из n равновозможных, попарно несовместимых событий, то вероятность события А есть , т.е.

P(A)= .

(1)

Иными словами, вероятность случайного события есть отношение числа исходов, благоприятствующих появлению события А, к числу всех исходов.

Пример 2. Брошена игральная кость. Найти вероятность выпадения четного числа очков (событие А).

Решение. Здесь полная группа событий состоит из шести событий: А₁, А₂, А₃, А₄, А₅, А₆, где А_i – выпало i очков. Событие А = А₂ + А₄ + А₆, таким образом, m=3, n=6.

P(A) = =

Пример 3. Бросаются две игральные кости. Найти вероятности появления того или иного числа очков.

Решение. При бросании двух игральных костей может выпасть любое число очков от двух до двенадцати. Полная группа событий состоит здесь из 36 событий и, если кости правильные, то выпадение каждой из 36 возможных комбинаций числа очков на первой и на второй кости можно считать равновозможным. Число очков равное 12 появляется в одном случае – на первой и на второй кости выпало по 6 очков; таким образом, вероятность выпадения 12 очков равна . Число очков равное 11 может появиться двумя способами: на первой кости 5 очков, на второй – 6, или на первой – 6 и на второй – 5; откуда вероятность появления 11 очков равна . Теперь без труда можно убедиться, что искомые вероятности задаются следующей таблицей:

Таблица 1

Число очков	2	3	4	5	6	7	8	9	10	11	12
Вероятность

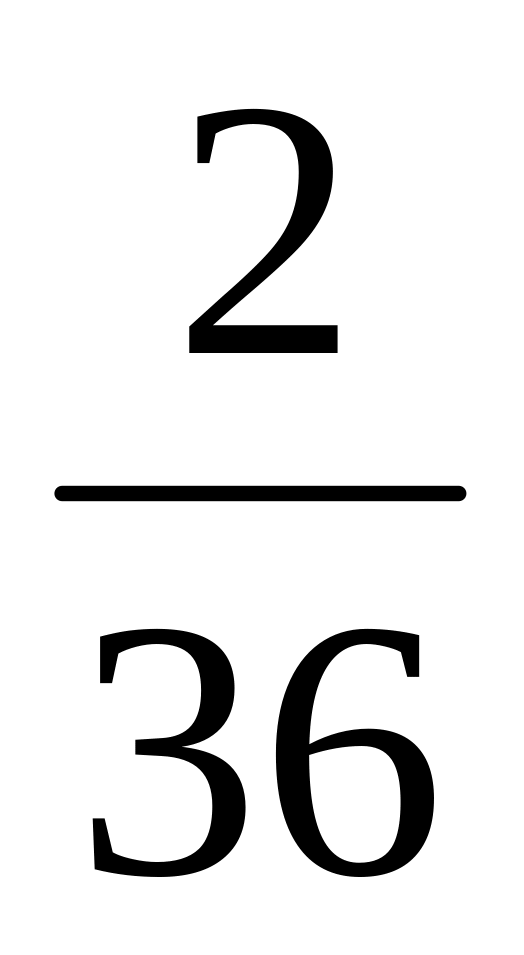
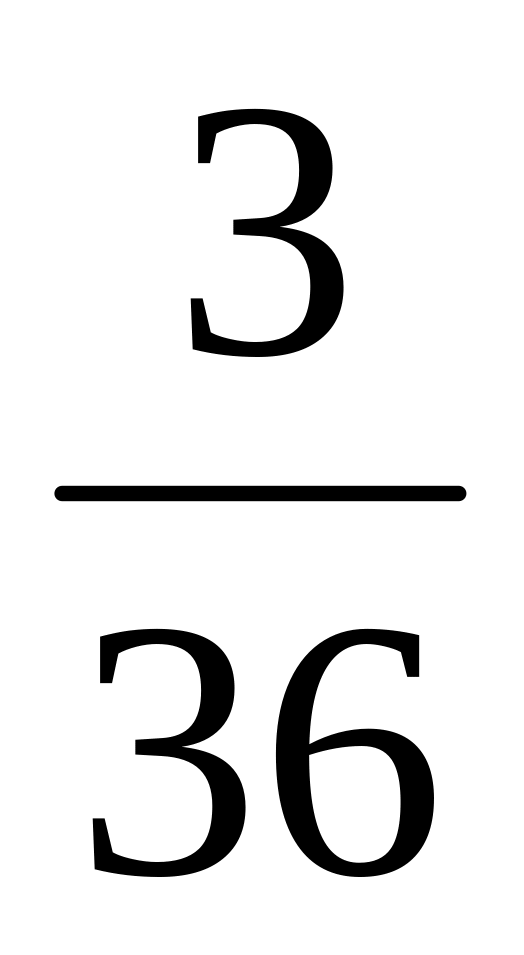
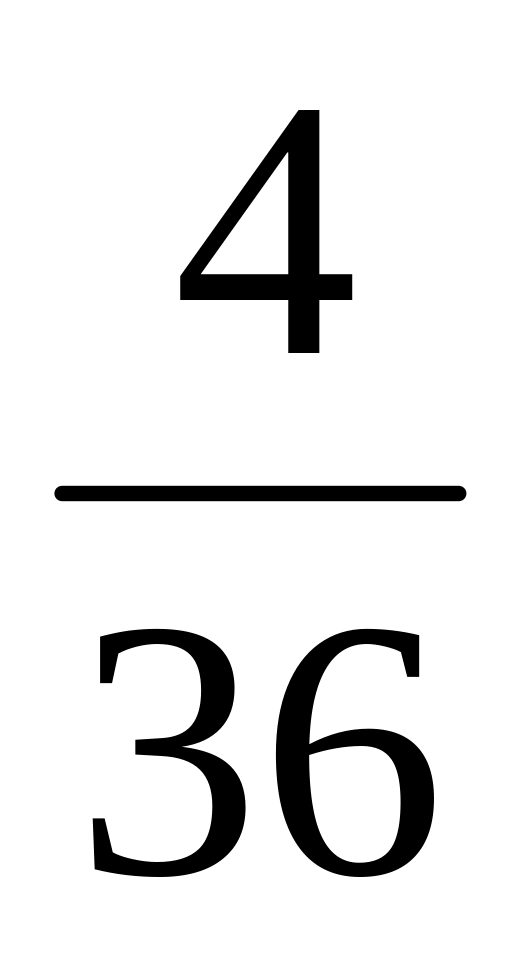
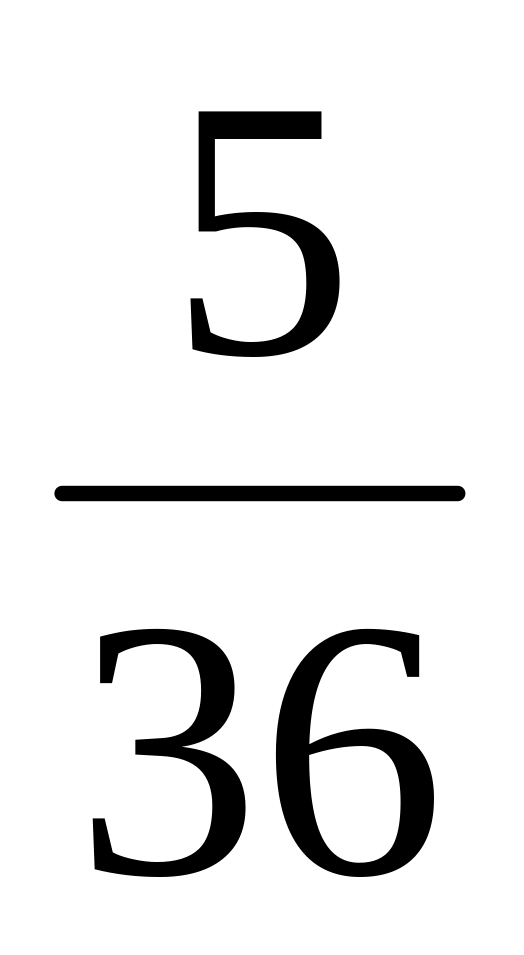
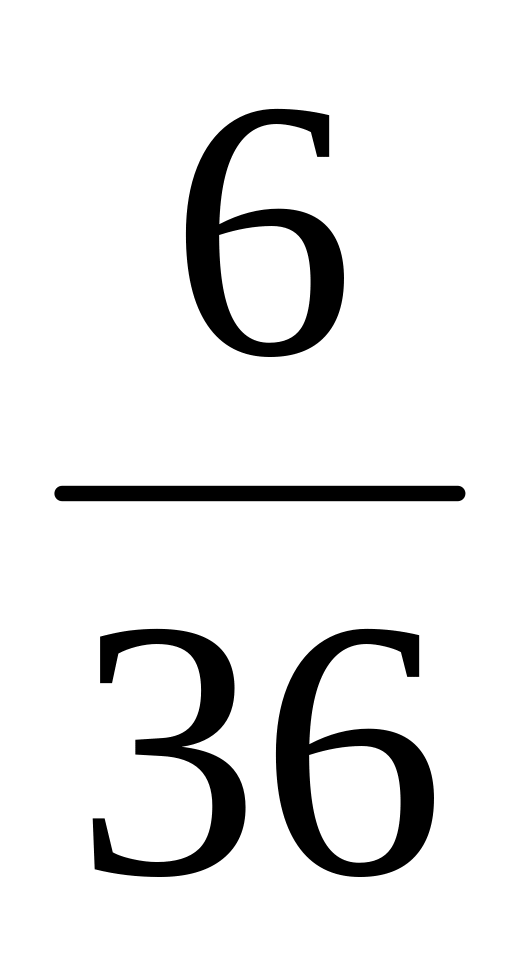
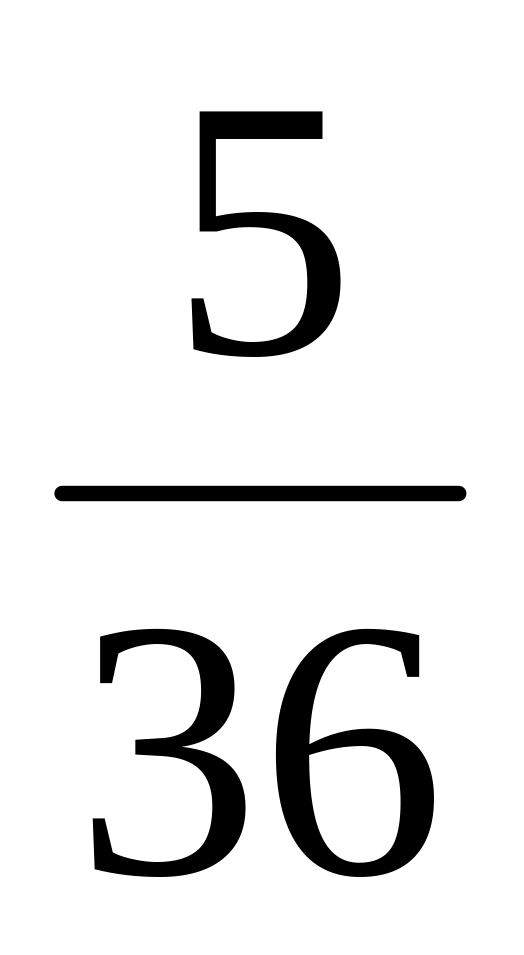
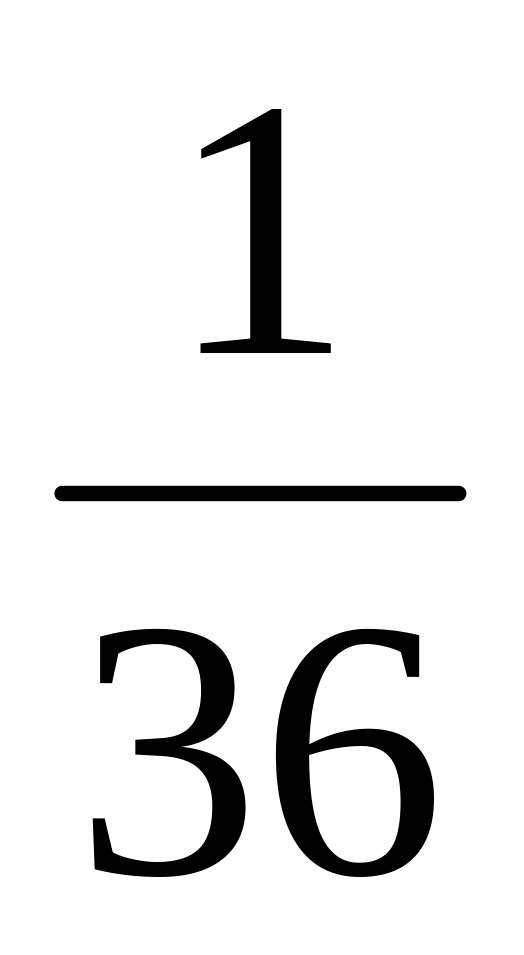
Перечислим все исходы, благоприятствующие появлению 7 очков: 1-6, 6-1, 5-2, 2-5, 3-4, 4-3; таким образом, их ровно 6.

При вычислении вероятностей случайных событий часто используется раздел элементарной математики – комбинаторики. Приведем основные формулы комбинаторики.

Пусть имеется конечно-элементное множество состоящее из n элементов.

Перестановками называются комбинации элементов множества, состоящие из всех n элементов и отличающиеся друг от друга только лишь их порядком. Для примера выпишем все перестановки трехэлементного множества a, b, c : abc, bac, bca, cba, cab, acb. Число перестановок n – элементного множества вычисляется по формуле:

Pn=n!,

(2)

где n! = 1 ·3·…·n (читается эн-факториал), причем полагают 0! = 1. При n = 3 получаем P₃ = 3! = 1·2·3 = 6.

Сочетанием из n элементов по k называются комбинации, состоящие ровно из k элементов и отличающиеся друг от друга хотя бы одним элементом. Число сочетаний из n по k (или что тоже самое – число различных k – элементных подмножеств n – элементного множества) обозначается символом С :

С = .

(3)

Выпишем все сочетания из четырех элементов по два: (n = 4, k = 2) ab, ac, ad, bc, bd, cd; следовательно,

C = = = 6.

Основное правило комбинаторики: если некоторый выбор N можно осуществить n способами, а некоторый выбор M можно осуществить m способами, то N и M вместе можно осуществить m·n способами.

Пример 4. Из урны, содержащей три белых и четыре черных шара, наудачу извлекаются три шара. Найдите вероятность появления двух белых и одного черного шаров (событие А).

Решение. Здесь число элементарных исходов равно числу способов извлечь 3 шара из 7, т.е. . Два белых шара (выбор М) извлекаются из трех способами; 1 черный шар можно извлечь четырьмя различными способами (выбор N); 2 белых и 1 черный можно выбрать 3 · 4 = 12 способами. Таким образом .

Свойства классической вероятности:

0 ≤ P(A) ≤ 1, p(U) =1, P(V) = 0.

(4)

Если А ·В = V, то

Р(А + В) = Р(А) + Р(В),

(5)

т.е. вероятность суммы несовместимых событий равна сумме вероятностей этих событий.

Из последнего свойства следует важная формула.

(6)

т.е. сумма вероятностей противоположных событий равна 1.