
- •Раздел. Математический анализ
- •Тема 1. Множества и функции в.1. Понятие множества
- •В.2. Абсолютная величина действительного числа. Окрестность точки
- •В.3. Определение функции
- •В.5. Элементарные функции
- •В.6. Интерполирование функций
- •В. 7. Преобразование графиков
- •Тема 2. Пределы и непрерывность в.1. Предел числовой последовательности
- •В.2. Предел функции
- •В. 3. Бесконечно малые величины
- •В. 4. Бесконечно большие величины
- •В. 5. Основные теоремы о пределах. Признаки существования предела
- •В. 6. Замечательные пределы
- •В.7. Непрерывность функции
- •В.8. Вычисление пределов
- •Тема 3. Дифференциальное исчисление функций одной переменной в.1. Задачи, приводящие к производной. Задача о касательной:
- •В.2. Определение производной функции
- •В.3. Основные правила дифференцирования
- •В.4. Производная сложной и обратной функций
- •В. 5. Производные основных элементарных функций
- •В.6. Производные высших порядков
- •В.7. Приложения производной
- •7.1. Правило Лопиталя
- •7.2. Возрастание и убывание функции. Экстремум функции
- •7.3. Исследование функции на выпуклость и точки перегиба
- •7.4. Асимптоты графика функции
- •9.4. Общая схема исследования функций и построения их графиков
- •В.8. Дифференциал функции
- •8.1. Определение дифференциала
- •8.2. Применение дифференциала в приближённых вычислениях
- •8.3. Дифференциалы высших порядков
- •Тема 4. Неопределенный интеграл (ни) в.1. Первообразная и неопределённый интеграл
- •В.3. Таблица ни
- •В.4. Методы интегрирования
- •4.1. Метод разложения
- •4.2. Метод замены переменной
- •4.3. Метод интегрирования по частям
- •В.5. Интегрирование отдельных классов функций
- •5.1. Интегрирование простейших рациональных дробей
- •5.2. Интегрирование иррациональных функций
- •5.3. Интегрирование тригонометрических функций
- •Тема 5. Определённый интеграл в.1. Формула Ньютона-Лейбница.
- •В.2. Замена переменной и интегрирование по частям в определенном интеграле.
В. 7. Преобразование графиков
Пусть задан график функции y = f(x). Тогда справедливы следующие утверждения:
График функции y = f(x+a) есть график y = f(x), сдвинутый на а единиц параллельно оси Оy (вдоль оси Oх); при a > 0 – влево, при a < 0 – вправо.
График функции y = f(x)+b есть график y = f(x), сдвинутый b единиц параллельно оси Оx (вдоль оси Oy); при b > 0 – вверх, при b < 0 – вниз.
График функции y = mf(x) (m≠0) есть график y = f(x), растянутый при m > 1 в m раз или сжатый при 0 < m <1 в m раз вдоль оси Oy. При m < 0 график функции y = mf(x) есть зеркальное отображение графика y = -mf(x) от оси Ox.
График функции y = f(kx) (k≠0) есть график y = f(x), сжатый при k > 1 в k раз или растянутый при 0 < k < 1 в k раз вдоль оси Ox. При k < 0 график функции y = f(-kx) есть зеркальное отображение графика y = f(kx) от оси Oy.
График функции
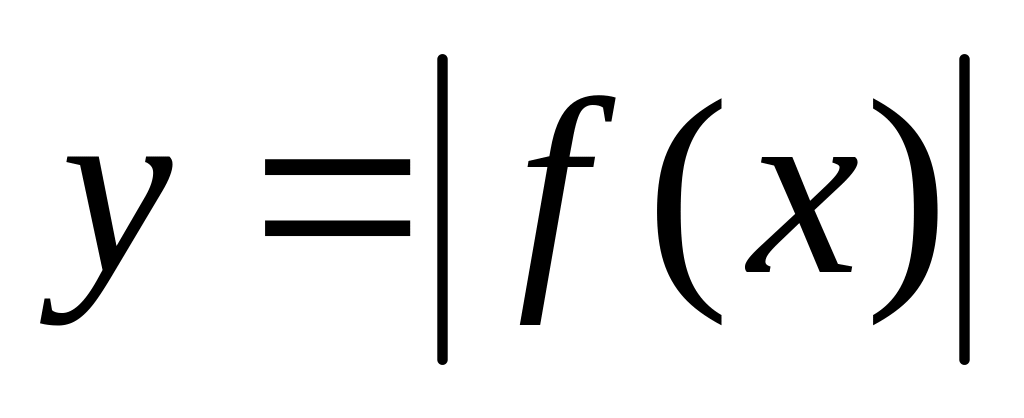 получается из графика функции y
= f(x), если
оставить на месте ту часть, где
f(x) ≥ 0 и
симметрично отобразить относительно
Ох
часть f(x)˂
0:
получается из графика функции y
= f(x), если
оставить на месте ту часть, где
f(x) ≥ 0 и
симметрично отобразить относительно
Ох
часть f(x)˂
0:
![]() .
.
6.
График функции
![]() совпадает с графиком y
= f(x)
на множеств неотрицательных значений
аргумента и симметричен ему относительно
Оу
на множестве отрицательных значений
аргумента.
совпадает с графиком y
= f(x)
на множеств неотрицательных значений
аргумента и симметричен ему относительно
Оу
на множестве отрицательных значений
аргумента.
Пример 4. Построить график функции у = –4∙sin2x + 1.
Р ешение.
1) Сначала построим график функции у
= sinx.
ешение.
1) Сначала построим график функции у
= sinx.
у

 1
1

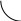
 О х
О х
-π -![]() -1
π
-1
π
2) Сжатием графика в 2 раза вдоль оси Ох получаем график функции у=sin2x.
у
1
 О х
О х
-π - π
3) Растянем график у = sin2x вдоль оси Оу в 4 раза и получим график функции
у
= 4sin2x.
 у
у
 4
4

 1
1
 О х
О х
-π - π
-4
4) Зеркально отобразив график от оси Ох, получим у = –4sin2x.
 у
у

 4
4
 1
1

 О х
О х
-π - π
-4
5) Сдвинем полученный график на 1 единицу вверх параллельно оси Оу. Таким образом график функции у = – 4∙sin2x + 1 имеет вид:
 у
у
5
1
π О π х
-3
Тема 2. Пределы и непрерывность в.1. Предел числовой последовательности
Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число an, то говорят, что задана числовая последовательность {an}:
a1, a2,…,an… .
Другими словами, числовая последовательность – это функция натурального аргумента an=f(n).
Числа a1, a2,…,an называются членами последовательности, а число an – общим или n-м членом данной последовательности.
Пример 1: а) 2, 4, 6, …2n, … (монотонная неограниченная);
б) 1, 0, 1, 0, … (немонотонная ограниченная);
в)
0,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
…,
,
…,
![]() ,
… - немонотонная, ограниченная. Изобразим
её точками числовой оси. С ростом n
последовательность как угодно близко
приближается к 1. При этом
,
… - немонотонная, ограниченная. Изобразим
её точками числовой оси. С ростом n
последовательность как угодно близко
приближается к 1. При этом
![]() ,
,
![]() ,
,
![]() ,
… ,
,
… ,
![]() ,
… Т.е. с ростом n
расстояние
,
… Т.е. с ростом n
расстояние
![]() будет меньше любого, сколь угодно малого
числа.
будет меньше любого, сколь угодно малого
числа.
Число А называется пределом числовой последовательности {an}, если для любого сколь угодно малого положительного числа > 0 найдется такой номер N(), зависящий от , что для всех членов данной последовательности с номерами n > N() верно неравенство an - A < .
Предел
числовой последовательности обозначается
![]() или
или
![]() .
Используя следующие логические символы
(кванторы):
(любой),
(существует),
(равносильность или эквивалентность),
определение предела можно записать в
виде:
.
Используя следующие логические символы
(кванторы):
(любой),
(существует),
(равносильность или эквивалентность),
определение предела можно записать в
виде:
(A
=
![]() an)
(
> 0
N()
: n
> N()
an
– A
< )
an)
(
> 0
N()
: n
> N()
an
– A
< )
Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.
Смысл определения: для достаточно больших n члены последовательности {an} сколь угодно мало отличаются от числа А.
