5. Пример расчета пластинки с использованием принципа минимума энергии деформации
Рассматривается задача о растяжении в своей плоскости прямоугольной пластинки напряжениями, приложенными вдоль ее краев по параболическому закону (см. рис. 7).
Пластинка растянута усилиями:
при
(парабола);
при
Нагрузка
вдоль оси, перпендикулярной плоскости
пластины, равна нулю, поэтому
В учебнике [7] утверждается, что энергия
деформации пластинки единичной толщины
в этом случае равна:
(9)
Рис. 7. Нагружение пластины в ее плоскости
Поскольку
распределение напряжений в прямоугольной
пластине не зависит от упругих констант
материала, положим в (9)
Введем функцию напряжений
следующим способом:
Тогда энергия пластинки выразится через функцию напряжений:
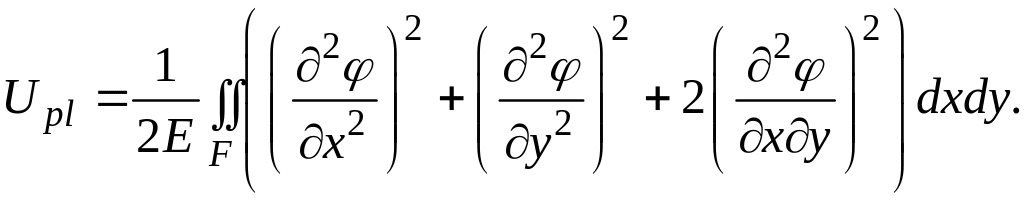
Функцию напряжений будем искать в виде:
.
При
этом все
должны удовлетворять краевым условиям,
а коэффициенты
находим из условий
… .
Пусть
при этом краевые условия выполнены.
Тогда получим уравнение для
Для квадратной пластинки со стороной :
Отсюда можно определить неизвестные напряжения.
Фактически при решении этой задачи использован метод Ритца.
Глава 5. Сложное напряженное состояние деформируемых тел
1. Свободная энергия стержня в общем случае нагружения
Пусть в сечении могут возникать все шесть силовых факторов:
N – нормальные усилия;
Qx, Qy – поперечные усилия;
Mx, My, Mz – изгибающие и крутящий моменты.
Найдем потенциальную энергию деформированного стержня при постоянной температуре, совпадающую со свободной энергией. Пусть точка приведения сил совпадает с центром тяжести сечения, а оси Ох и Оу – главные оси сечения.
Рис. 8. Силовые факторы в сечении стержня для осей y, z
Тогда изменение потенциальной энергий элемента dz при деформировании можно представить как сумму элементарных работ внутренних сил на перемещении:
dU = dU(Mк) + dU(Mx) + dU(My)+ dU(N) + dU(Qx) + dU(Qy)
Приведем известные формулы вычисления силовых факторов через напряжения:
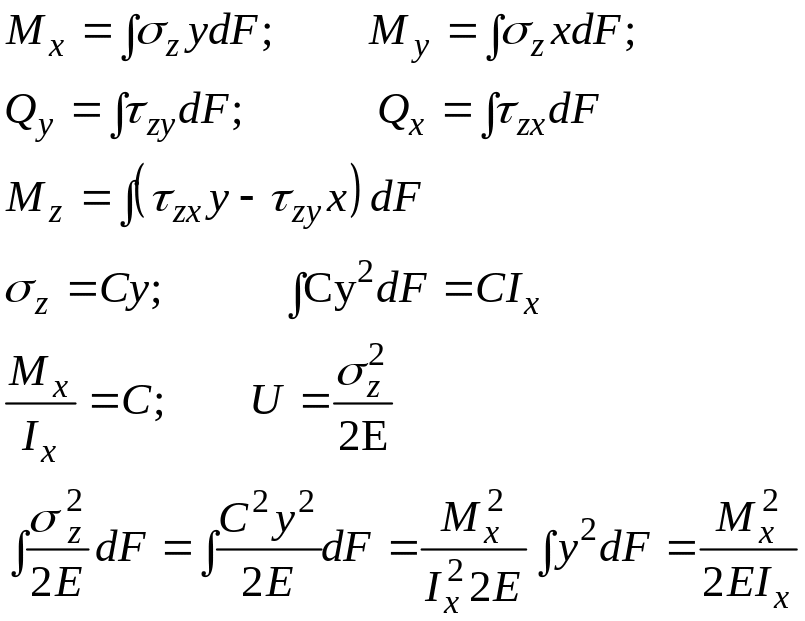
Е – модуль Юнга при сжатии;
G – модуль упругости при сдвиге.
Для кручения;
Ранее были получены формулы для энергии деформации «чистых» состояний растяжения, кручения и изгиба:
Будем
применять эти формулы для сложного
сопряженного состояния. Найдем dU
(Qy). Рассмотрим призму с
площадью основания dF и
длиной dz. Энергия объема
равна
,
где
– удельная энергия.
При
сдвиге
Интегрируя
по площади F:
Можно
показать, что
–
формула
Журавского; где
–
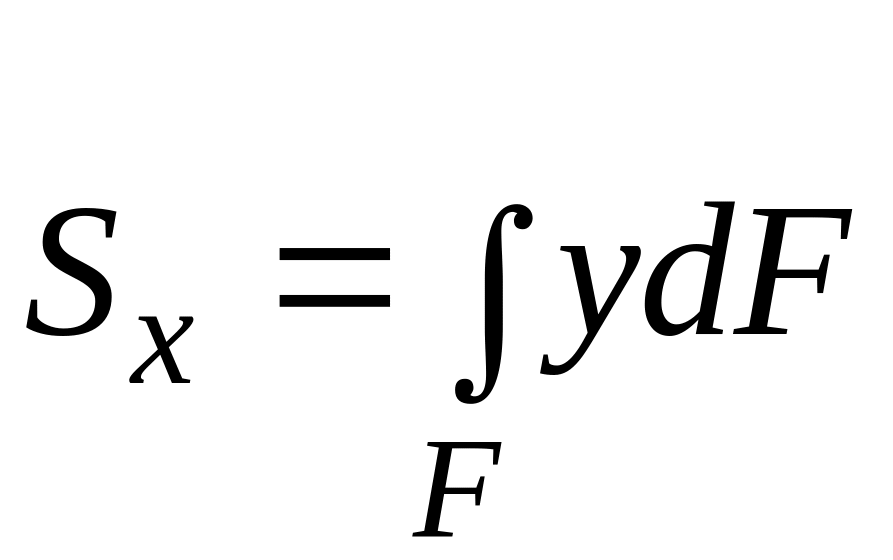статистический момент
сечения; Ix
–
момент
инерции относительно оси
Ох
=
;
b
= b(y)
– текущая ширина сечения.
Отсюда получим
где
–
константа, зависящая только от формы
сечения.
Аналогично
.
Для прямоугольного сечения kx =ky = 6/5.
Для сплошного круга k = 10/9.
Для тонкостенного круга k = 2.
Тогда получим:
Как правило, для стержневых систем, работающих на изгиб и кручение, три последних слагаемых малы, и ими можно пренебречь. Для таких систем
.
2. Теорема Кастилиано
Теорема. Частная производная от потенциальной энергии системы по силе равна перемещению точки приложения силы по направлению этой силы.
Pn – обобщенная сила; n – обобщенное перемещение, на котором Рn совершает работу, т. е., если Рn – внешний момент, то n – угол поворота.
Ограничение: должен выполняться закон Гука, в отличие от теоремы Лагранжа. Для сплошной среды:
– тоже
теорема Кастилиано.
Пример 1. Определить при помощи теоремы Кастилиано угол поворота правого торца стержня, нагруженного моментом Мкр.
Решение
Внутренняя энергия стержня:
Это совпадает с известным выражением для .
Пример 2. Определить прогиб консоли, нагруженной силой Р.
П
отенциальная
энергия при изгибе:
На расстоянии z от точки приложения силы Р
По теореме Кастилиано искомое перемещение:
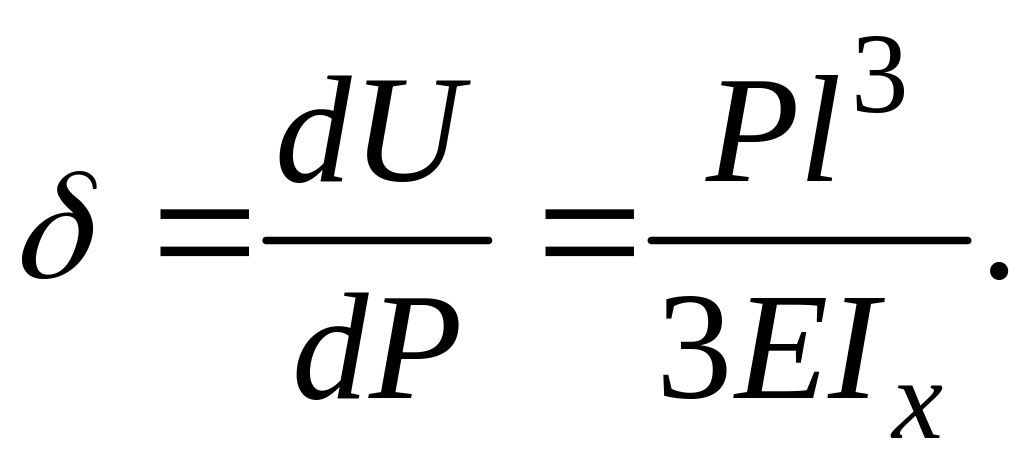
Этот результат можно получить интегрированием уравнения упругой линии балки.