
- •Специальные главы механики деформируемых тел
- •Введение
- •Глава 1. Деформации и напряжения в тонкой пластине
- •Основные понятия и гипотезы
- •Перемещения и деформации в пластинке
- •Напряжения в пластинке
- •Усилия в тонкой пластинке
- •5. Вывод уравнений равновесия пластинки
- •Глава 2. Уравнения равновесия тонкой пластины
- •Формулировка граничных условий
- •Изгиб круглой пластинки
- •Глава 3. Равновесие прямоугольной пластины
- •Глава 4. Прочность пластин. Применение вариационных принципов к расчету пластин
- •Энергия тонкой пластинки
- •2. Критерий прочности тонкой пластинки
- •3. Деформационный критерий несущей способности пластин
- •4. Вариационные принципы при расчете пластин
- •5. Пример расчета пластинки с использованием принципа минимума энергии деформации
- •Глава 5. Сложное напряженное состояние деформируемых тел
- •1. Свободная энергия стержня в общем случае нагружения
- •2. Теорема Кастилиано
- •3. Интеграл Мора
- •Глава 6. Упругопластическое кручение и изгиб стержня
- •Условия пластичности. Состояние пластичности
- •Идеальная пластичность
- •Упругопластический изгиб призматического бруса
- •Упругопластическое кручение круглого бруса
- •Кручение некруглых стержней
- •Глава 7. Исследование напряженного состояния
- •Напряжения в наклонном сечении при растяжении (одноосное напряженное состояние).
- •Двуосное напряженное состояние.
- •Плоское напряженное состояние.
- •4. Главные напряжения.
- •5. Круг Мора для двуосного напряженного состояния
- •Круг Мора для плоского напряженного состояния
- •Деформация при двуосном напряженном состоянии
- •Глава 8. Основы механики разрушения
- •1. История и литература. Исходная задача об эллиптическом отверстии.
- •2. Энергия деформации пластинки с отверстием и коэффициент интенсивности напряжений
- •3. Критическое равновесие трещины
- •4. Схема расчета на трещиностойкость
- •5. Учет пластической зоны
- •6. Учет конечности размеров пластины
- •7. Экспериментальное определение коэффициента интенсивности напряжений
- •Заключение
- •Рекомендуемый библиографический список
- •Содержание
- •Специальные главы механики деформируемых тел
- •680021, Г. Хабаровск, ул. Серышева, 47.
Глава 1. Деформации и напряжения в тонкой пластине
Основные понятия и гипотезы
Определение 1. Пластиной называется призматическое или цилиндрическое тело, высота которого мала по сравнению с размерами в плане.
Определение 2. Плоскость, делящая пластинку пополам по толщине, называется срединной. Линия пересечения боковой поверхности со срединной плоскостью называется контуром пластинки.
Координаты:
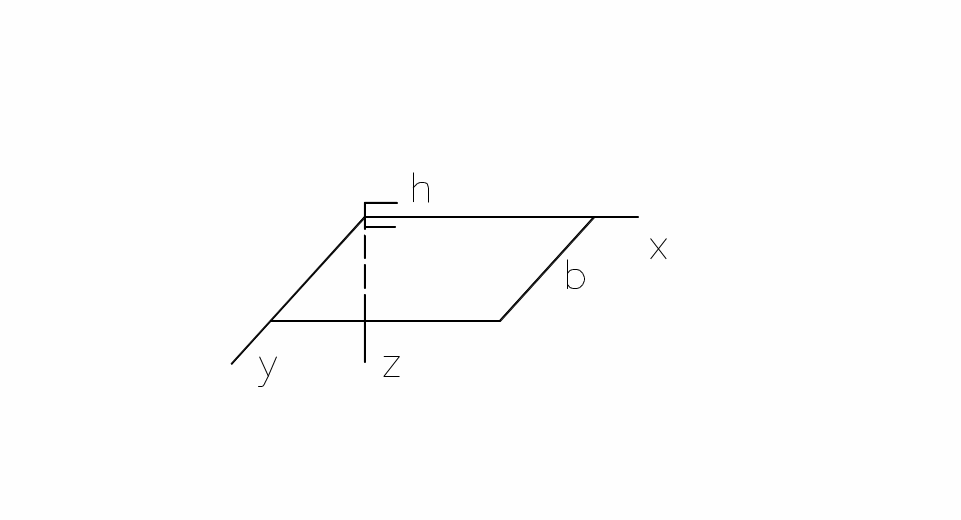
Рис. 1. Координатные линии
![]() в
срединной плоскости,
в
срединной плоскости,
![]() вертикально
вниз.
вертикально
вниз.
![]() прогиб
пластинки (перемещение вдоль
прогиб
пластинки (перемещение вдоль
![]() ).
).
Пластинка
считается тонкой, если:
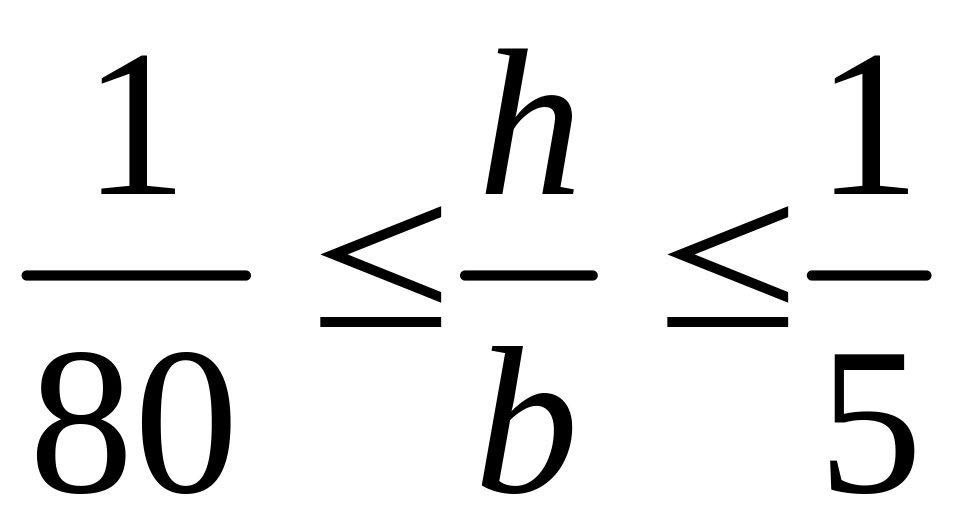 ;
;
![]()
Допустимо
считать тонкой пластинку, в которой
выполнено
![]() .
.
Если
![]() ,
то применяют теорию гибких пластин.
,
то применяют теорию гибких пластин.
Гипотезы теории пластин:
Гипотеза прямых нормалей. Сдвиги в плоскостях
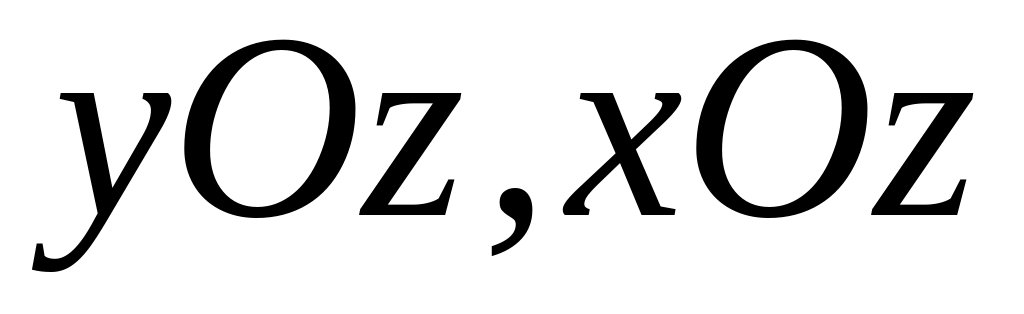 отсутствуют:
отсутствуют:
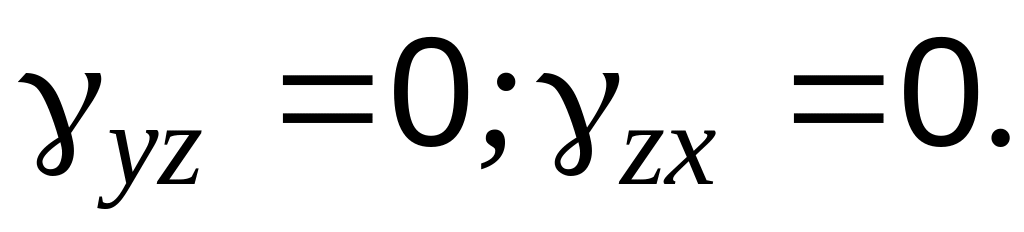 Нет деформации вдоль
:
Нет деформации вдоль
:
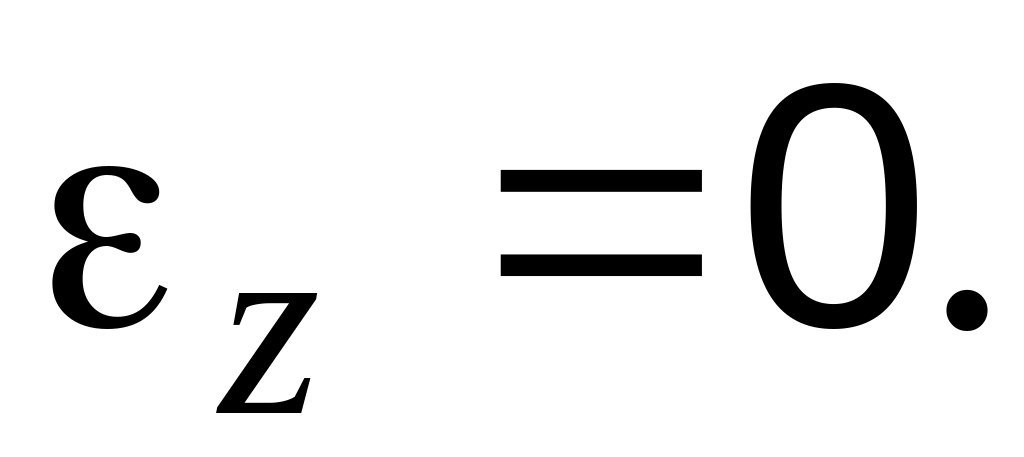
Гипотеза о недеформируемости срединной плоскости:
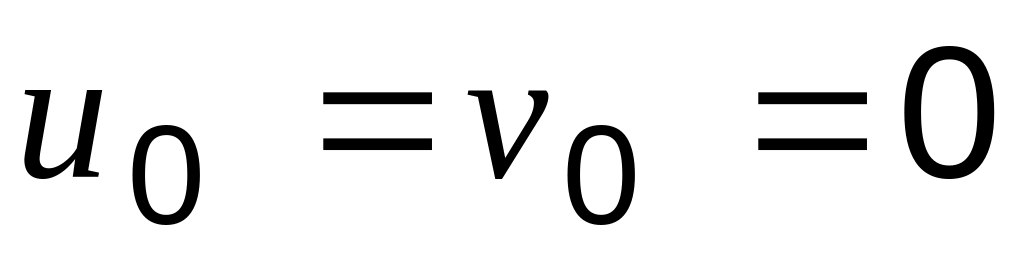 .
.Гипотеза об отсутствии давления между слоями пластинки, параллельными срединной плоскости:
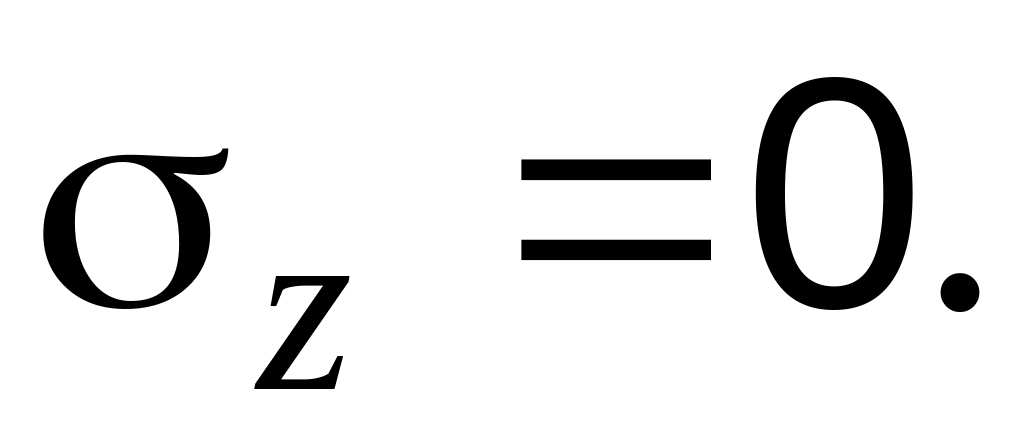
Перемещения и деформации в пластинке
Как
правило, из уравнений равновесия находят
прогиб пластинки
![]() .
Выразим деформации через этот прогиб.
.
Выразим деформации через этот прогиб.
Для получения этих выражений нам понадобятся формулы Коши, выражающие деформации через перемещения:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
(1)
;
(1)
![]() ;
;
![]() .
.
![]() ,
следовательно,
,
следовательно,
![]() – из уравнений Коши.
– из уравнений Коши.
Это
означает, что
![]() прогиб не зависит от координаты
прогиб не зависит от координаты
![]() .
.
Из
![]() следует
следует
![]()
![]()
Поскольку не зависит от , проинтегрируем эти уравнения по :
![]() ;
;
![]() .
.
Из
того, что при
![]() (на срединной поверхности)
,
следует
(на срединной поверхности)
,
следует
![]() .
.
Отсюда получим
![]() ;
;
![]() .
.
Ненулевые деформации из формул Коши равны:
![]() ;
;
![]() ;
(2)
;
(2)
![]() ;
;
В этих уравнениях деформации выражены через прогибы .
Напряжения в пластинке
По
предположению,
![]() .
.
Закон Гука для нормальных напряжений
![]() ;
;
![]() .
.
Решая
систему относительно
![]() ,
,
![]() ,
и учитывая (2):
,
и учитывая (2):
![]() ;
;
![]() ,
откуда
,
откуда
![]() ;
;
![]() .
(3)
.
(3)
Закон Гука для сдвиговых напряжений
![]() .
.
Оказывается,
пользоваться законом Гука при определении
![]() ,
,
![]() нельзя, поскольку тогда получим
=
= 0, согласно гипотезе прямых нормалей.
Воспользуемся непосредственно уравнениями
равновесия из теории упругости,
пренебрегая объемными силами:
нельзя, поскольку тогда получим
=
= 0, согласно гипотезе прямых нормалей.
Воспользуемся непосредственно уравнениями
равновесия из теории упругости,
пренебрегая объемными силами:
![]()
Используя (3), получим:
![]()
Интегрируя по :
![]() .
.
Здесь
![]() – оператор Лапласа.
– оператор Лапласа.
Считая,
что на верхней и нижней плоскостях нет
касательных нагрузок, т. е.
![]() =
0 при
=
0 при
![]() ,
найдем
,
найдем
![]()
Подставляя
![]() в формулу для
,
получим
в формулу для
,
получим
![]()
Тем же путем получим
![]() (4)
(4)
Таким образом, напряжения выражены через прогибы формулами (3), (4). Ниже приведены эпюры напряжений в зависимости от вертикальной координаты в соответствии с выведенными формулами.
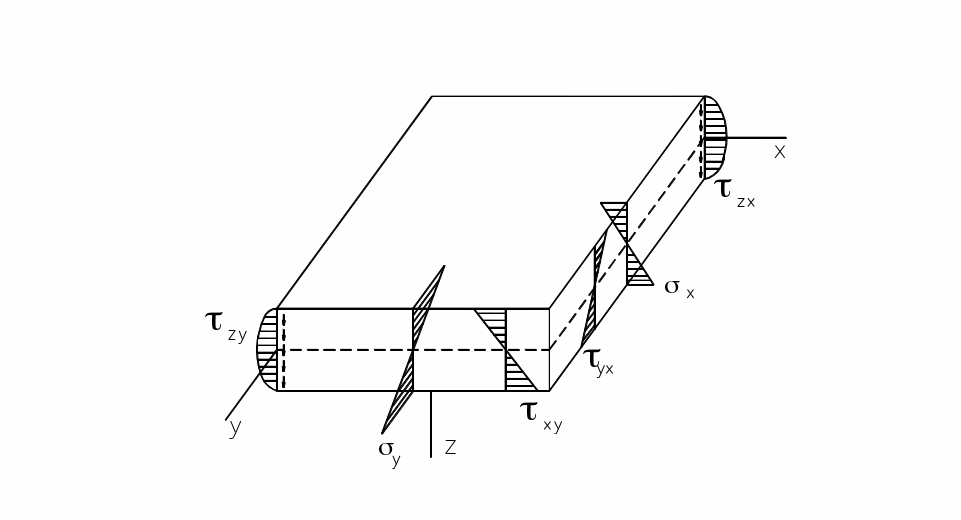
Рис. 2. Эпюры напряжений по толщине пластины
Усилия в тонкой пластинке
Найдем
внутренние силовые факторы в сечении,
перпендикулярном оси
![]() :
:

Рис. 3. Внутренние силовые факторы
![]() – изгибающий
момент.
– изгибающий
момент.
![]() – крутящий
момент.
– крутящий
момент.
![]() – поперечная
сила.
– поперечная
сила.
Все
силы рассматриваются на единицу ширины
пластины (т. е. делим на размер вдоль
![]() ).
).
По
определению
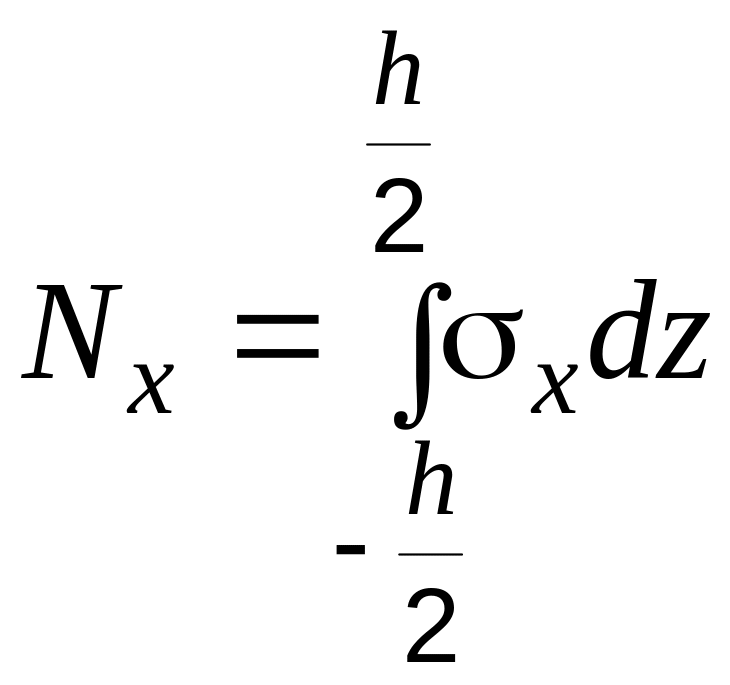 .
Из (3) получим:
.
Из (3) получим:
 .
.
Изгибающий момент по определению:
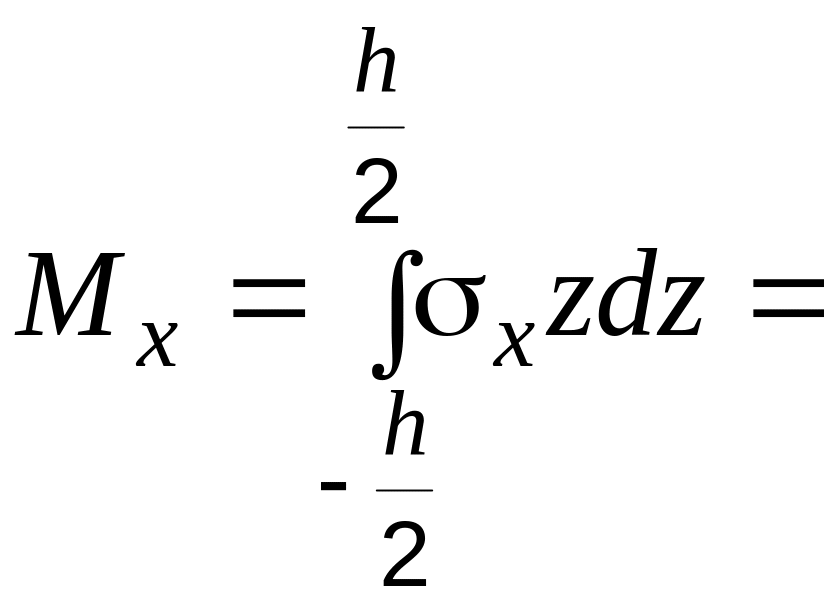
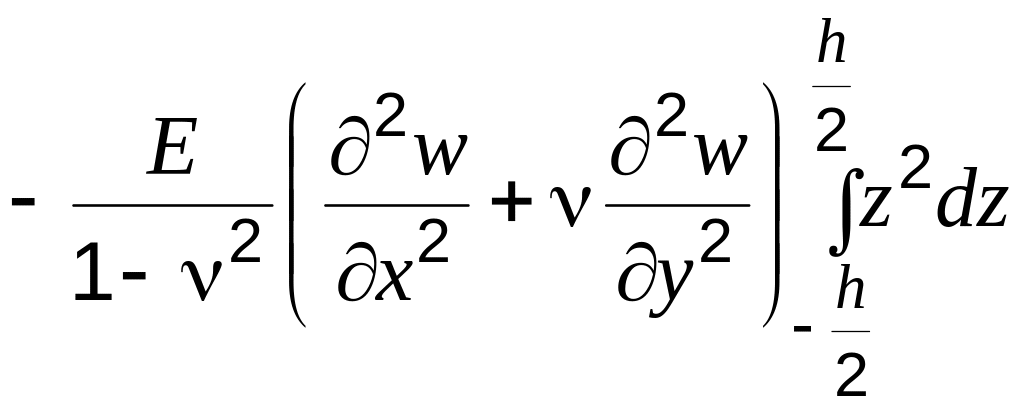 .
.
![]() .
(5)
.
(5)
Далее обозначим
![]() – цилиндрическая
жесткость пластины.
– цилиндрическая
жесткость пластины.
Единицы
измерения изгибающего момента
![]() на единицу ширины.
на единицу ширины.
Поперечная сила:
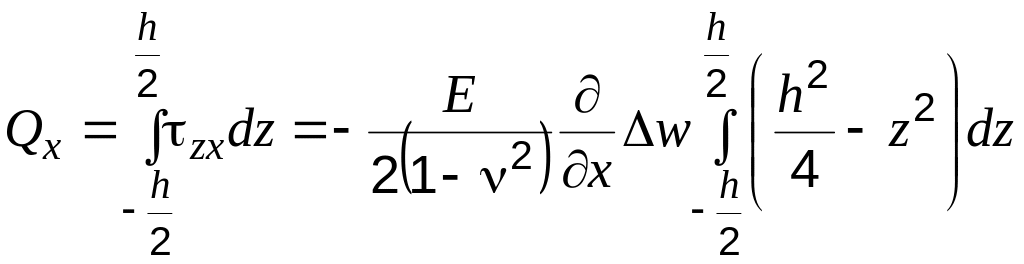 .
.
Проинтегрировав, получим:
![]() .
.
Единицы
измерения:
![]() на единицу ширины.
на единицу ширины.
Крутящий момент:
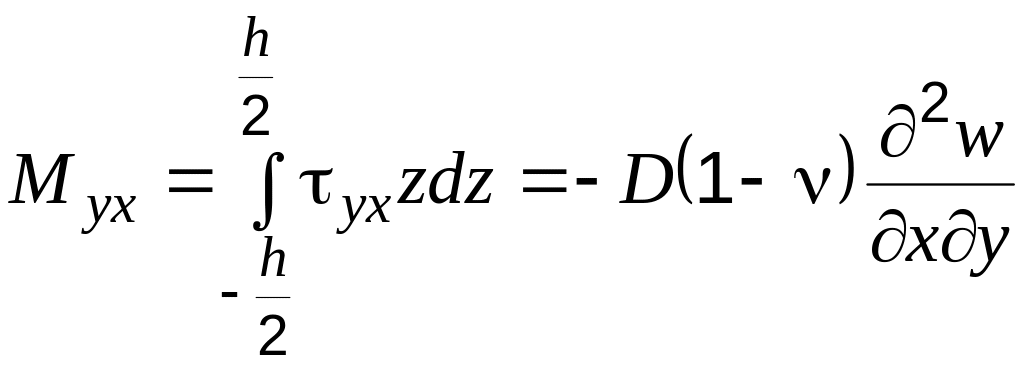 .
.
Единицы
измерения:
![]() на единицу ширины.
на единицу ширины.
Аналогично найдем
![]() ;
;
![]() ;
(6)
;
(6)
![]() .
.
Заметим, что
![]() ,
как и должно быть по третьему закону
Ньютона.
,
как и должно быть по третьему закону
Ньютона.
Формулы (5), (6) связывают усилия в пластинке с прогибами срединной плоскости. Осталось найти прогибы.
