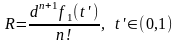- •1.Неопределенный интеграл.
- •2. Первообразные элем.Функций.
- •3.Замена переменных в неопр.Интегралле.
- •4.Интегрирование по частям.
- •5.Интегрирование иррациональных функций.
- •6.Элементарные рац.Функции и интегралы от них.
- •7.Алгоритм
- •8.Интегрирование функций, содержащих радикалы.
- •9.Интегрирование биноминальных дифференциалов.
- •11.Тригонометрическая подстановка.
- •12.Интегр.Функций содержащих показ.Функции
- •13.Определенный интеграл.
- •14.Класс интегрируемых функций
- •15.Определенный интеграл как функция верхнего предела
- •16.Теорема: (Теорема Ньютона – Лейбница)
- •17.Замена переменных.
- •18.Интегрирование по частям.
- •19.Приложения опред. Интеграла
- •1)Площадь плоской фигуры.
- •22.Интеграл Эйлера I рода
- •23.Интеграл Эйлера I I рода
- •24.Функции нескольких переменных
- •25. Непрерывные функции
- •26.Дифференцирование функций нескольких переменных.
- •27.Производная сложной функции
- •28.Частные дифференциалы и дифференциал функции
- •29.Частные производные высших порядков.
- •30.Дифференциалы высших порядков.
- •31.Формула Тейлора
- •32.Градиент.
- •33.Экстремум функции нескольких переменных.
- •34.Теорема. (Достаточные условия экстремума).
- •35.Условный экстремум.
- •36.Билинейная и квадратичная форма
- •38.Второй дифф.Как квадрат.Форма
- •39.Пространства.
- •40.Основные понятия теории дифференциальных уравнений.
- •41.Дифференциальные уравнения первого порядка
- •42.Уравнения с разделяющимися переменными.
- •43.Однородное дифференциальное уравнение первого порядка.
- •44.Уравнения, приводящиеся к однородным. К таким уравнениям относят уравнения вида:
- •45.Линейное уравнение первого порядка
- •46.Уравнение Бернулли
- •47.Уравнение Риккати
- •48.Уравнение в полных дифференциалах и их решение
- •49.Интегральный множитель и его нахождение
- •50.Дифференциального уравнения n-го порядка.
- •51.Диф.Ур.Высшего порядка.Способы пониж.Порядка
- •Уравнения, не содержащие явно искомой функции
- •52.Линейные однородные дифференциальные уравнения с
- •Линейные неоднородные дифференциальные уравнения с произвольными коэффициентами.
- •54.Метод вариации
- •55.Метод неопределенных коэффициентов.
- •56.Метод Коши
- •57.Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.
- •58.Нормальные системы обыкновенных дифференциальных уравнений.
- •59.Метод сведения к одному уравнению.
- •60.Метод интегрируемых комбинаций
- •61. Нормальные системы обыкновенных дифференциальных уравнений.
- •62.Фундаментальная система решений как базис линейного пространства решений однородной линейной системы
- •68.Определитель Вронского
- •64.Системы линейных уравнений первого порядка с постоянными коэффициентами: однородные и неоднородные. Структура решения. Алгоритм решения.
- •65.Преобразование Лапласа.
- •66.Интегралл Лапласа и его свойства
- •67.Свойства 1-6 преобразования Лапласа.
- •68.Свойства 7-12 преобразования Лапласа.
- •70.Таблица изображений некоторых функций.
- •72.Интеграл Дюамеля
- •73.Достаточные условия существования оригинала
- •75.Решение уравнений методом Дюамеля.
28.Частные дифференциалы и дифференциал функции
Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке x0, а функция g имеет производную в точке y0 = f(x0), то сложная функция h(x) = g(f(x)) также имеет производную в точке x0.
Дифференциал
гладкой вещественнозначной функции f
определённой на M (M — область в
![]() или гладкое многообразие) представляет
собой 1-форму и обычно обозначается df
и определяется соотношением
или гладкое многообразие) представляет
собой 1-форму и обычно обозначается df
и определяется соотношением
![]()
где
![]() обозначает производную f по направлению
вектора X в касательном расслоении M.
обозначает производную f по направлению
вектора X в касательном расслоении M.
29.Частные производные высших порядков.
Если
функция f(x,
y)
определена в некоторой области D,
то ее частные производные
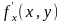 и
и
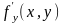 тоже будут определены в той же области
или ее части.
тоже будут определены в той же области
или ее части.
Будем называть эти производные частными производными первого порядка.
Производные этих функций будут частными производными второго порядка.
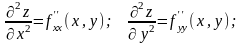

Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.
Определение.
Частные производные вида
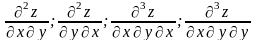
 и
т.д. называются смешанными
производными.
и
т.д. называются смешанными
производными.
Теорема.
Если функция f(x,
y)
и ее частные производные
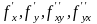 определены и непрерывны в точке М(х, у)
и ее окрестности, то верно соотношение:
определены и непрерывны в точке М(х, у)
и ее окрестности, то верно соотношение:
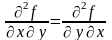 .
.
Т.е. частные производные высших порядков не зависят от порядка дифференцирования.
Аналогично определяются дифференциалы высших порядков.
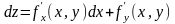
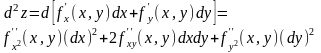
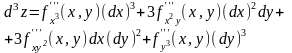
…………………
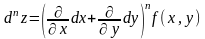
Здесь n – символическая степень производной, на которую заменяется реальная степень после возведения в нее стоящего с скобках выражения.
30.Дифференциалы высших порядков.
Определение: Дифференциалом порядка k, k>1 от функции f(x,y) в точке (x0,y0) называется дифференциал от дифференциала порядка k-1.
…………………
Здесь n – символическая степень производной, на которую заменяется реальная степень после возведения в нее стоящего с скобках выражения.
31.Формула Тейлора
Теорема. Пусть функция f(x,y) и все её частные производные до порядка n+1 непрерывны в некоторой окрестности точки (x0,y0). Тогда справедлива формула Тейлора:
 где
dx=x-x0,
dy=y-y0
и
где
dx=x-x0,
dy=y-y0
и
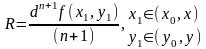 - остаток в форме Лагранжа.
- остаток в форме Лагранжа.
Пусть точка (x,y) лежит в рассматриваемой окрестности точки (x0,y0). Сделаем следующую замену переменных:
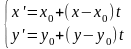
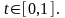
Зафиксируем значения x и y. Тогда справедлива формула Тейлора для функции f1(x)=f(x’,y’) в точке t=0:
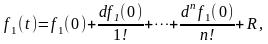 где
где