50.Дифференциального уравнения n-го порядка.

Дифференциальным уравнением называется равенство вида

F(x, y, y', …, y⁽ⁿ⁾) = 0,

где F(t₁, t₂, …, t_n+2)  функция (n+2)-х переменных, выражающая связь между аргументом x, неизвестной функцией y и ее производными. Порядок n старшей производной, входящей в уравнении, называется порядком уравнения (конечно, не все участники, приведенные в определении, могут реально входить в уравнение: некоторые из производных, и также сама функция y(x) или даже аргумент x могут в уравнении явно не присутствовать).

Общий вид дифференциального уравнения первого порядка выглядит так:

F(x, y, y') = 0.

семейство функций y = (x, C₁, C₂, ..., C_n) называется общим решением дифферециального уравнения n-го порядка, если при любом выборе значений C₁, C₂, ..., C_n оно является частным решением уравнения. В п. 1.7. выяснится, почему число постоянных C_i должно быть именно равным порядку n.

Теорема существования и единственности для дифференциального уравнения n-го порядка.

Пусть дан (n+1)-мерный параллелепипед  = {(x₁,…,x_n+1) | a_i<x_i<b_i для всех i=1,…,n+1} и функция f (x₁,…,x_n+1), непрерывная и имеющая непрерывные производные 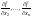всюду в области . Тогда для любой точки (x₀;y₀;y'₀;…;y₀⁽ⁿ⁺¹⁾) области  существует единственное решение дифференциального уравнения

y⁽ⁿ⁾ = f(x, y, y', …, y^(n-1)),

удовлетворяющее начальным условиям y(x₀) = y₀, y'(x₀) = y'₀,…, y⁽ⁿ⁺¹⁾(x₀) = y₀⁽ⁿ⁺¹⁾.

51.Диф.Ур.Высшего порядка.Способы пониж.Порядка

Понижение порядка дифференциального уравнения – основной метод решения уравнений высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем уравнениям. Рассмотрим случаи, когда возможно понижение порядка.

Уравнения вида y⁽ⁿ⁾ = f(x).

Если f(x) – функция непрерывная на некотором промежутке a < x < b, то решение может быть найдено последовательным интегрированием.

…………………………………………………………….

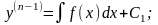
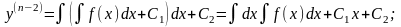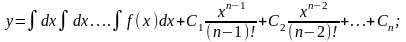
Уравнения, не содержащие явно искомой функции

и ее производных до порядка k – 1 включительно.

Это уравнения вида:

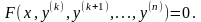
В уравнениях такого типа возможно понижение порядка на k единиц. Для этого производят замену переменной:

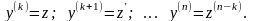
Тогда получаем:

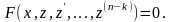
Теперь допустим, что полученное дифференциальное уравнение проинтегрировано и совокупность его решений выражается соотношением:

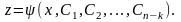
Делая обратную подстановку, имеем:

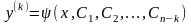
Интегрируя полученное соотношение последовательно k раз, получаем окончательный ответ:

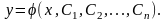
Уравнения, не содержащие явно независимой переменной.

Это уравнения вида

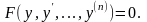
Порядок таких уравнений может быть понижен на единицу с помощью замены переменных

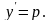
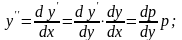
и т.д.

Подставляя эти значения в исходное дифференциальное уравнение, получаем:

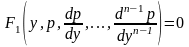
Если это уравнение проинтегрировать, и 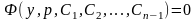- совокупность его решений, то для решения данного дифференциального уравнения остается решить уравнение первого порядка: