17.Замена переменных.

Пусть задан интеграл 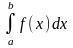, где f(x) – непрерывная функция на отрезке [a, b].

Введем новую переменную в соответствии с формулой x = (t).

Тогда если

1) () = а, () = b

2) (t) и (t) непрерывны на отрезке [, ]

3) f((t)) определена на отрезке [, ], то

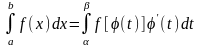
Тогда 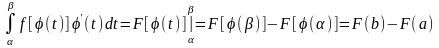При замене переменной в определенном интеграле следует помнить о том, что вводимая функция (в рассмотренном примере это функция sin) должна быть непрерывна на отрезке интегрирования. В противном случае формальное применение формулы приводит к абсурду.

18.Интегрирование по частям.

Если функции u = (x) и v = (x) непрерывны на отрезке [a, b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:

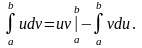
Способ основан на известной формуле производной произведения:

(uv) = uv + vu

где u и v – некоторые функции от х.

В дифференциальной форме: d(uv) = udv + vdu

Проинтегрировав, получаем: , а в соответствии с приведенными выше свойствами неопределенного интеграла:

или ;

Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.

19.Приложения опред. Интеграла

1)Площадь плоской фигуры.

Площадь криволинейной трапеции, ограниченной неотрицательной функцией f (x), осью абсцисс и прямыми x = a, x = b, определяется как

Площадь фигуры, ограниченной функцией f (x), пересекающей ось абсцисс, определяется формулой

где xi – нули функции. Другими словами, чтобы вычислить площадь этой фигуры, нужно разбить отрезок [a; b] нулями функции f (x) на части, проинтегрировать функцию f по каждому из получившихся промежутков знакопостоянства, сложить отдельно интегралы по отрезкам, на которых функция f принимает разные знаки, и вычесть из первого второе.

2)Длина дуги кривой.

Пусть задана кривая Тогда длина ее участка, ограниченного значениями t = α и t = β выражается формулой

В частности, длина плоской кривой, задаваемой на координатной плоскости OXY уравнением y = f (x), a ≤ x ≤ b, выражается формулой

3)Объем тела вращения.

Пусть тело образовано вращением вокруг оси OX криволинейной трапеции, ограниченной непрерывной на отрезке [a; b] функцией f (x). Его объем выражается формулой

Пусть тело заключено между плоскостями x = a и x = b, а площадь его сечения плоскостью, проходящей через точку x, – непрерывная на отрезке [a; b] функция σ (x). Тогда его объем равен

4)Площадь в полярных координатах

Напомним, что определением интеграла служит предел интегральных сумм, взятый при условии измельчения разбиения отрезка интегрирования. Этим определением мы воспользуемся для нахождения площади в следующем случае.

Площадь кругового сектора подсчитывается по формуле

Более кратко эту формулу можно записать так:

5)Масса проволоки через плотность.

20.Несобственные интегралы первого рода

Пусть

1. функция 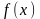определена на отрезке ;

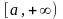2. 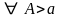 существует .

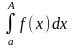Произведем теперь предельный переход 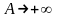. Тогда 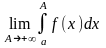называется несобственным интегралом первого рода и обозначается символом :

= .

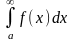Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится (или: существует). Если этот предел равен бесконечности или вообще не существует, то говорят, что несобственный интеграл расходится (или: не существует).

Совершенно аналогично определяются и следующие несобственные интегралы первого рода:

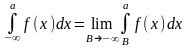
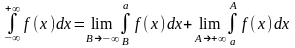(а  любое).

Пример.

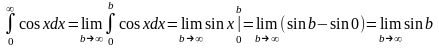- не существует.

Несобственный интеграл расходится.

Пример.

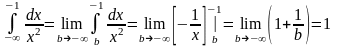- интеграл сходится

21.Несобственные интегралы второго рода.

Пусть с есть особая точка функции и 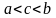. Тогда, как уже говорилось выше,

.

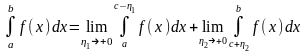Снова обратите внимание на то, что в этом определении два предела и величины ₁ и ₂ никак друг с другом не связаны. Главное значение этого интеграла определяется так

,

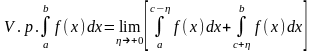то есть величины ₁ и ₂ стали одинаковыми и предел один.

Рассмотрим пример на вычисление главного значения. Пусть мы имеем интеграл 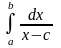и . Тогда имеем

.

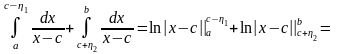
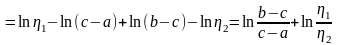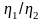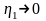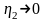Но если ₁ и ₂ никак друг с другом не связаны, то отношение может быть любым, и при , предел не существует. Но если считать, что ₁ = ₂, то 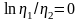и поэтому

,

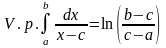и интеграл существует в смысле главного значения.