- •1.Неопределенный интеграл.
- •2. Первообразные элем.Функций.
- •3.Замена переменных в неопр.Интегралле.
- •4.Интегрирование по частям.
- •5.Интегрирование иррациональных функций.
- •6.Элементарные рац.Функции и интегралы от них.
- •7.Алгоритм
- •8.Интегрирование функций, содержащих радикалы.
- •9.Интегрирование биноминальных дифференциалов.
- •11.Тригонометрическая подстановка.
- •12.Интегр.Функций содержащих показ.Функции
- •13.Определенный интеграл.
- •14.Класс интегрируемых функций
- •15.Определенный интеграл как функция верхнего предела
- •16.Теорема: (Теорема Ньютона – Лейбница)
- •17.Замена переменных.
- •18.Интегрирование по частям.
- •19.Приложения опред. Интеграла
- •1)Площадь плоской фигуры.
- •22.Интеграл Эйлера I рода
- •23.Интеграл Эйлера I I рода
- •24.Функции нескольких переменных
- •25. Непрерывные функции
- •26.Дифференцирование функций нескольких переменных.
- •27.Производная сложной функции
- •28.Частные дифференциалы и дифференциал функции
- •29.Частные производные высших порядков.
- •30.Дифференциалы высших порядков.
- •31.Формула Тейлора
- •32.Градиент.
- •33.Экстремум функции нескольких переменных.
- •34.Теорема. (Достаточные условия экстремума).
- •35.Условный экстремум.
- •36.Билинейная и квадратичная форма
- •38.Второй дифф.Как квадрат.Форма
- •39.Пространства.
- •40.Основные понятия теории дифференциальных уравнений.
- •41.Дифференциальные уравнения первого порядка
- •42.Уравнения с разделяющимися переменными.
- •43.Однородное дифференциальное уравнение первого порядка.
- •44.Уравнения, приводящиеся к однородным. К таким уравнениям относят уравнения вида:
- •45.Линейное уравнение первого порядка
- •46.Уравнение Бернулли
- •47.Уравнение Риккати
- •48.Уравнение в полных дифференциалах и их решение
- •49.Интегральный множитель и его нахождение
- •50.Дифференциального уравнения n-го порядка.
- •51.Диф.Ур.Высшего порядка.Способы пониж.Порядка
- •Уравнения, не содержащие явно искомой функции
- •52.Линейные однородные дифференциальные уравнения с
- •Линейные неоднородные дифференциальные уравнения с произвольными коэффициентами.
- •54.Метод вариации
- •55.Метод неопределенных коэффициентов.
- •56.Метод Коши
- •57.Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.
- •58.Нормальные системы обыкновенных дифференциальных уравнений.
- •59.Метод сведения к одному уравнению.
- •60.Метод интегрируемых комбинаций
- •61. Нормальные системы обыкновенных дифференциальных уравнений.
- •62.Фундаментальная система решений как базис линейного пространства решений однородной линейной системы
- •68.Определитель Вронского
- •64.Системы линейных уравнений первого порядка с постоянными коэффициентами: однородные и неоднородные. Структура решения. Алгоритм решения.
- •65.Преобразование Лапласа.
- •66.Интегралл Лапласа и его свойства
- •67.Свойства 1-6 преобразования Лапласа.
- •68.Свойства 7-12 преобразования Лапласа.
- •70.Таблица изображений некоторых функций.
- •72.Интеграл Дюамеля
- •73.Достаточные условия существования оригинала
- •75.Решение уравнений методом Дюамеля.
4.Интегрирование по частям.
Способ основан на известной формуле производной произведения:
(uv) = uv + vu
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав,
получаем:
 ,
а в соответствии с приведенными выше
свойствами неопределенного интеграла:
,
а в соответствии с приведенными выше
свойствами неопределенного интеграла:
 или
или
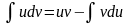 ;
;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Пример.
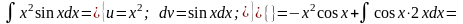
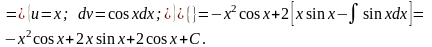
Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.
Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.
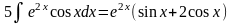
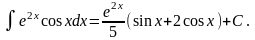
Таким образом, интеграл найден вообще без применения таблиц интегралов.
5.Интегрирование иррациональных функций.
Интегрирование некоторых иррациональных функций.
Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой может быть найден как известно всегда.
Рассмотрим некоторые приемы для интегрирования различных типов иррациональных функций.
Интеграл
вида
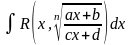 где
n-
натуральное число.
где
n-
натуральное число.
С помощью
подстановки
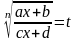 функция рационализируется.
функция рационализируется.
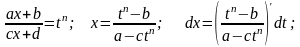
Тогда
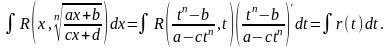
Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.
6.Элементарные рац.Функции и интегралы от них.
Прежде
всего напомним, что любой многочлен
Q(x)
с
действительными коэффициентами,
коэффициент при старшей степени которого
равен единице, может быть разложен
(каким образом - это уже другой вопрос)
в произведение многочленов с
действительными коэффициентами вида
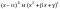 ,
где квадратные трехчлены
,
где квадратные трехчлены
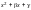 не имеют действительных корней.
не имеют действительных корней.
Так как интеграл от суммы функций равен сумме интегралов от слагаемых, и интегрирование многочлена не представляет труда, то проблема интегрирования рациональных дробей сводится к проблеме интегрирования правильных рациональных дробей.
Среди совокупности всех правильных рациональных дробей мы выделим класс так называемых простейших рациональных дробей. Правильную рациональную дробь назовем простейшей, если она имеет один из следующих видов:
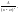 и
без степени 2)…
и
без степени 2)…
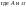 -
произвольные
действительные числа; k
- натуральное
число,
-
произвольные
действительные числа; k
- натуральное
число,
3)
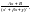 и без степени 4)
и без степени 4)
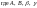 -
действительные
числа; k
-
натуральное
число, и квадратный трехчлен
-
действительные
числа; k
-
натуральное
число, и квадратный трехчлен
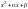
 не
имеет действительных корней (т.е. его
дискриминант
не
имеет действительных корней (т.е. его
дискриминант
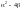 отрицателен).
отрицателен).
Решение происходит след.образом: выделяется полный квадрат знаменателя и выделяется табличный интеграл.