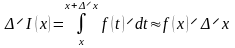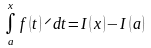- •1.Неопределенный интеграл.
- •2. Первообразные элем.Функций.
- •3.Замена переменных в неопр.Интегралле.
- •4.Интегрирование по частям.
- •5.Интегрирование иррациональных функций.
- •6.Элементарные рац.Функции и интегралы от них.
- •7.Алгоритм
- •8.Интегрирование функций, содержащих радикалы.
- •9.Интегрирование биноминальных дифференциалов.
- •11.Тригонометрическая подстановка.
- •12.Интегр.Функций содержащих показ.Функции
- •13.Определенный интеграл.
- •14.Класс интегрируемых функций
- •15.Определенный интеграл как функция верхнего предела
- •16.Теорема: (Теорема Ньютона – Лейбница)
- •17.Замена переменных.
- •18.Интегрирование по частям.
- •19.Приложения опред. Интеграла
- •1)Площадь плоской фигуры.
- •22.Интеграл Эйлера I рода
- •23.Интеграл Эйлера I I рода
- •24.Функции нескольких переменных
- •25. Непрерывные функции
- •26.Дифференцирование функций нескольких переменных.
- •27.Производная сложной функции
- •28.Частные дифференциалы и дифференциал функции
- •29.Частные производные высших порядков.
- •30.Дифференциалы высших порядков.
- •31.Формула Тейлора
- •32.Градиент.
- •33.Экстремум функции нескольких переменных.
- •34.Теорема. (Достаточные условия экстремума).
- •35.Условный экстремум.
- •36.Билинейная и квадратичная форма
- •38.Второй дифф.Как квадрат.Форма
- •39.Пространства.
- •40.Основные понятия теории дифференциальных уравнений.
- •41.Дифференциальные уравнения первого порядка
- •42.Уравнения с разделяющимися переменными.
- •43.Однородное дифференциальное уравнение первого порядка.
- •44.Уравнения, приводящиеся к однородным. К таким уравнениям относят уравнения вида:
- •45.Линейное уравнение первого порядка
- •46.Уравнение Бернулли
- •47.Уравнение Риккати
- •48.Уравнение в полных дифференциалах и их решение
- •49.Интегральный множитель и его нахождение
- •50.Дифференциального уравнения n-го порядка.
- •51.Диф.Ур.Высшего порядка.Способы пониж.Порядка
- •Уравнения, не содержащие явно искомой функции
- •52.Линейные однородные дифференциальные уравнения с
- •Линейные неоднородные дифференциальные уравнения с произвольными коэффициентами.
- •54.Метод вариации
- •55.Метод неопределенных коэффициентов.
- •56.Метод Коши
- •57.Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.
- •58.Нормальные системы обыкновенных дифференциальных уравнений.
- •59.Метод сведения к одному уравнению.
- •60.Метод интегрируемых комбинаций
- •61. Нормальные системы обыкновенных дифференциальных уравнений.
- •62.Фундаментальная система решений как базис линейного пространства решений однородной линейной системы
- •68.Определитель Вронского
- •64.Системы линейных уравнений первого порядка с постоянными коэффициентами: однородные и неоднородные. Структура решения. Алгоритм решения.
- •65.Преобразование Лапласа.
- •66.Интегралл Лапласа и его свойства
- •67.Свойства 1-6 преобразования Лапласа.
- •68.Свойства 7-12 преобразования Лапласа.
- •70.Таблица изображений некоторых функций.
- •72.Интеграл Дюамеля
- •73.Достаточные условия существования оригинала
- •75.Решение уравнений методом Дюамеля.
11.Тригонометрическая подстановка.
Интегралы от дифф. такого вида берутся с помощью так называемой универсальной тригоном. подстановки.
Теорема:
Интеграл вида
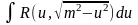 подстановкой
подстановкой
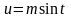 или
или
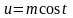 сводится к интегралу
от рациональной функции относительно
sint
или cost.
сводится к интегралу
от рациональной функции относительно
sint
или cost.
Теорема:
Интеграл вида
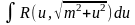 подстановкой
подстановкой
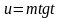 или
или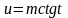 сводится к интегралу от рациональной
функции относительно sint
и cost.
сводится к интегралу от рациональной
функции относительно sint
и cost.
Теорема:
Интеграл вида
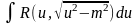 подстановкой
подстановкой
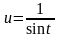 или
или
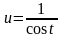 сводится к интегралу от рациональной
функции относительно sint
или cost.
сводится к интегралу от рациональной
функции относительно sint
или cost.
12.Интегр.Функций содержащих показ.Функции
13.Определенный интеграл.
Пусть
функция
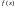 определена на интервале
определена на интервале
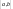 .
Выберем разбиение отрезка
.
Выберем разбиение отрезка
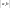 с помощью точек
с помощью точек
 на более мелкие отрезки
на более мелкие отрезки
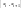 .
Внутри каждого из последних отрезков
выберем точку
.
Внутри каждого из последних отрезков
выберем точку
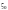 .
Тогда число, равное
.
Тогда число, равное
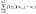 ,
называется соответствующей интегральной
суммой.
,
называется соответствующей интегральной
суммой.
Определение:
Если при любых разбиениях отрезка [a,
b]
таких, что maxxi
0 и произвольном
выборе точек i
интегральная сумма
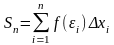 стремится к пределу S,
который называется определенным
интегралом от f(x)
на отрезке [a,
b].
стремится к пределу S,
который называется определенным
интегралом от f(x)
на отрезке [a,
b].
Обозначение
:
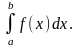
а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования.
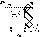
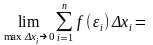
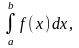 то функция называется интегрируемой
на отрезке [a,
b].
то функция называется интегрируемой
на отрезке [a,
b].
Также
верны утверждения:
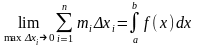

Теорема: Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
Свойства определенного интеграла.
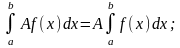
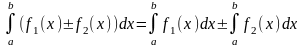
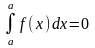
Если f(x) (x) на отрезке [a, b] a < b, то
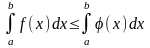
Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:

14.Класс интегрируемых функций
1)Если функция непрерывна на отрезке то она не определена.
2)Если ограничена на отрезке и имеет определённое число точек то она интегрируема
3)Монотонная функция интегрируема если она ограничена на интервале (а,в).
Теорема о среднем значении.
Пусть f(x) интегрируема на [a,b] где (a,b)- ориент.интервал на всём [a,b] функция f(x) ограничена на [a,b]
Любое
X
принадлежащее [a,b]
m≤f(x)≤M
тогда существует µ принадлежащее |R
(m≤µ≤M)
что
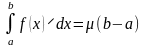
µ-среднее значение функции на интервале (a,b)