Алгоритм Басакера-Гоуэна (Basaker r.G., Gowen p.J)
Шаг
0. Решение
начинаем с нулевого потока
.
Полагаем
.
Шаг
1. Строим
граф модифицированных стоимостей
нет ни одной цепи из s в t, то задача
нахождения потока минимальной стоимости,
имеющего заданную мощность,
не имеет решения. В исходной сети G
пропущен поток максимальной мощности
минимальной стоимости. В противном
случае находим кратчайшую цепь
из s в t (роль длин дуг играют их
модифицированные стоимости).
Шаг
3. В исходном
графе определяем
-
путь P, соответствующий цепи P*. На прямых
дугах пути P вычисляем:
на обратных:
.
Находим
.
На прямых дугах пути P величину потока увеличиваем, а на обратных уменьшаем на .
Шаг
4 Полагаем
.
Если
,
то переходим к шагу 1, если
,
то алгоритм свою работу закончил, в сети
построен оптимальный поток.
Замечание. Для решения задачи о нахождении максимального потока максимальной стоимости достаточно в алгоритме Басакера-Гоуэна заменить на .
Пример.
Построить
поток заданной мощности
=3
минимальной стоимости в сети
(см. Рис. 1.24).
Итерация 1
Полагаем
.
Строим граф модифицированных стоимостей
(см. Рис. 1.25).
Находим кратчайшую (наиболее дешевую) цепь P* из s в t:
P*: s b a t,
Длина цепи (модифицированная стоимость) равна 3.
Соответствующий ей (s, t) – путь
P: s b a t,
и
.
Т.к. все дуги пути — прямые, то увеличивая пути P величину потока на 2, то получаем (см. Рис. 1.26)
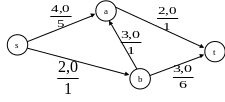
Рис. 1.24
Рис. 1.25
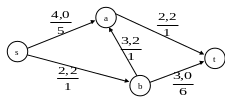
Рис. 1.26
Пересчитываем
.
Поскольку
,
то переходим к шагу 1.
Итерация 2
Стром
граф модифицированных стоимостей
(см.
Рис. 1.27).
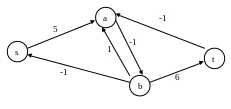
Рис. 1.27
Находим в графе модифицированных стоимостей кратчайшую цепь
P*: s a b t,
Соответствующий ей (s, t) – путь
P:
s
a
b
t.
На прямых дугах пути P вычисляем:
,
на обратных:
.
Находим
.
Величину потока на прямых дугах (s, a), (b, t) увеличиваем, а на обратной (a, b) уменьшаем на 1.
Получаем (см. Рис. 1.28)
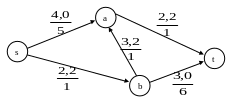
Рис. 1.28
Считаем
.
Т.к. , то алгоритм свою работу закончил, в сети построен оптимальный поток.
Вычислим суммарную стоимость пропущенного потока:
S(f)=1*5+1*2+1*1+1*2+6*1=16.
Очевидно, что при достаточно больших значениях использование алгоритма Басакера-Гоуэна приводит к длительным вычислениям.
Следующий алгоритм, предложенный Клейном, позволяет эти вычисления сократить.
Алгоритм Клейна (Klein m.)
Шаг 0. Решение начинаем с любого потока f из источника в сток мощности . Это может быть сделано подбором или с помощью задачи о максимальном потоке (в котором надо проводить вычисления до тех пор, пока величина потока не станет равной ). Вычисляем стоимость пропущенного потока f по формуле:
Шаг 1. Строим граф модифицированных стоимостей .
Шаг
2. Находим в
графе
ориентированный цикл отрицательной
длины
.
Если в графе модифицированных стоимостей
нет ни одного цикла отрицательной длины,
то задача решена: в сети построен поток
минимальной стоимости
мощности
.
В противном случае переходим к шагу 3.
Шаг 3. В исходной сети G определяем замкнутый путь P, соответствующий циклу P*. Прямыми дугами в этом цикле считаем дуги сонаправленные соответствующим дугам цикла P* в графе , обратными — дуги, имеющие противоположную ориентацию. На прямых дугах пути P вычисляем:
на обратных: .
Находим
.
На прямых дугах пути P величину потока увеличиваем, а на обратных уменьшаем на .
Шаг
4. Пересчитываем
и переходим к шагу 1.
Пример. Построить поток заданной мощности =5 минимальной стоимости в сети G (см. рис. 1.29):
В сети построен поток мощности =4. Пропускаем ещё одну единицу потока, получаем (см. рис. 1.30)
Итерация 1
Находим
=1*3+2*3+2*3+3*2+8*2=37.
Строим граф модифицированных стоимостей
(см.
рис. 1.31)
Находим цикл отрицательной длины P* (можно воспользоваться алгоритмом Флойда):
P*: b t c b,
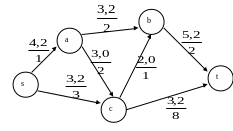
Рис. 1.29
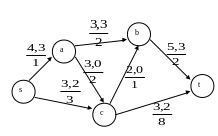
Рис. 1.30
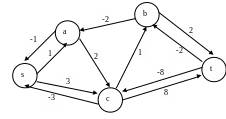
Рис. 1.31
Длина
цикла
.
Соответствующий ему путь в сети G: P:
b
t
c
b.
На прямых дугах пути P((b, t), (c, b)) вычисляем:
На обратной (t, c)
.
Находим
.
Величину потока на прямых дугах увеличиваем, а на обратной — уменьшаем на 2. Получаем: (см. рис. 1.32)
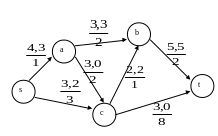
Рис. 1.32
Находим стоимость нового потока:
.
Итерация 2
Строим граф модифицированных стоимостей (см. рис. 1.33).
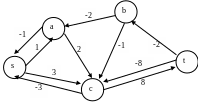
Рис. 1.33
В построенном графе отсутствуют циклы отрицательной длины.
Упражнение: Доказать этот факт при помощи алгоритма Флойда.
Т.о., в данной сети построен оптимальный поток, его стоимость равна 27.
Очевидно, что оба рассмотренных алгоритма позволяют найти поток мощность , если это число не превышает максимальной мощности допустимых потоков. Менее очевидно, что эти алгоритмы позволяют найти оптимальный поток. Доказательство этого факта основано на следующей теореме, которая может рассматриваться как основная теорема в теории потоков минимальной стоимости.
Теорема. Поток величины оптимален тогда и только тогда, когда граф модифицированных стоимостей не содержит ориентированных циклов отрицательной длины.
Упражнения
Пусть
—
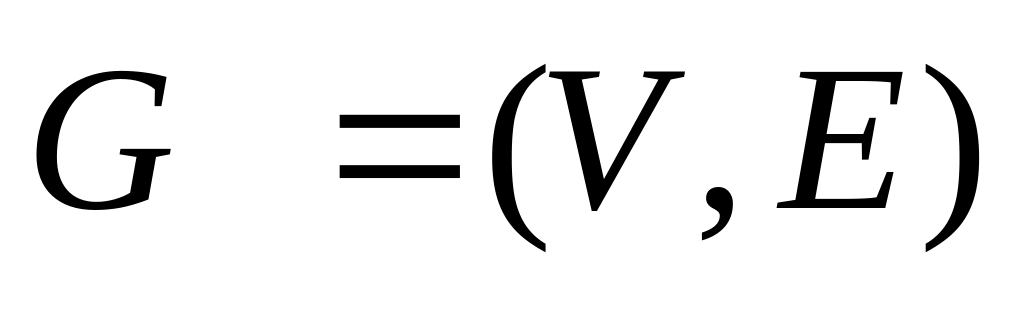сеть, с заданными пропускными способностями
,
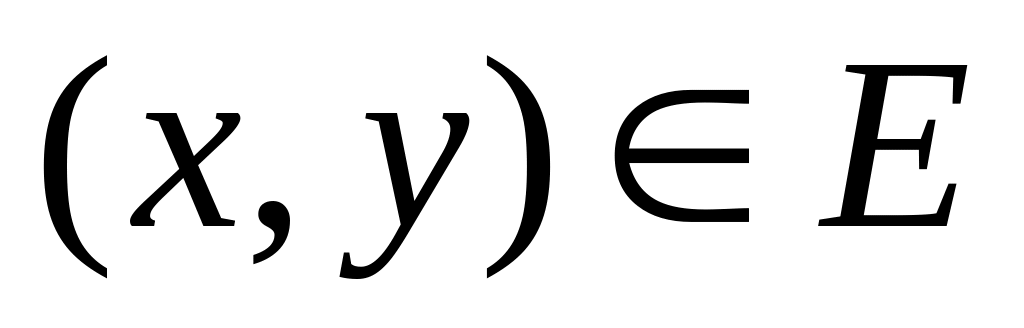и стоимостями
,
дуг. Среди допустимых потоков заданной
мощности
найти поток минимальной стоимости
.
Решить эту задачу при помощи модификации
алгоритма Басакера-Гоуэна.Пусть задана сеть, в которой мощность максимального потока равна . Известно, что стоимость провоза единицы потока по дуге (x, y) равна d(x,y), а пропускная способность дуги равна c(x,y).
Пусть известно, что мощность максимального потока в сети должна быть равной
,
.
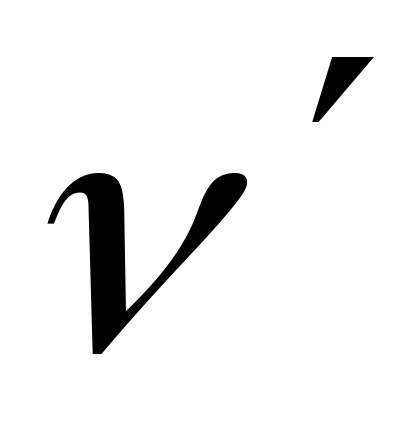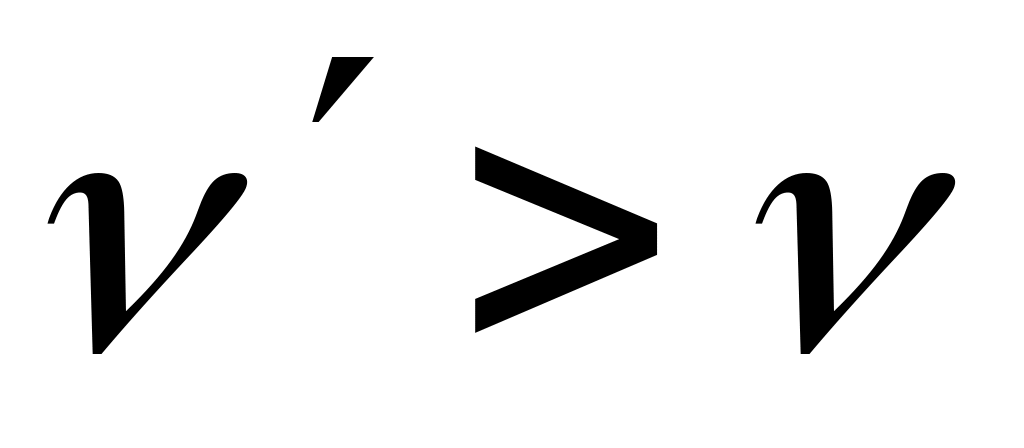Каким образом следует увеличить
пропускные способности дуг, чтобы
получить необходимый поток с минимальными
затратами (то есть с минимальным
увеличением стоимости потока)?Пусть известно, что суммарные затраты на пропущенный в сети поток не должны превышать заданной величины S. Как следует увеличить пропускные способности дуг, чтобы в преобразованной сети можно было бы пропустить поток как можно большей мощности?
В задаче о потоке минимальной стоимости поток является оптимальным тогда и только тогда, когда в графе модифицированных стоимостей не существует отрицательных циклов. Объяснить, почему при поиске максимального потока минимальной стоимости, граф можно разбить на две части и в каждой из них отдельно искать отрицательные циклы.