6. Дискретное программирование.

6.1 Метод Гомори для решения задачи целочисленного линейного программирования

Задачей целочисленноголинейного программирования (ЗЦЛП) называют ЗЛП, в которой на переменные налагается дополнительное ограничение – условие целочисленности. ЗЦЛП имеет вид:

(1)

(2)

(3)

- целые числа; (4)

где N₁ – некоторое подмножество множества индексов N =1,2, …,n.

Если N₁=N, то задачу (1) – (4) называют полностью целочисленной, если N₁N, - частично целочисленной.

Метод Гомори является одним из методов решения задач целочисленного линейного программирования. Идея метода Гомори решения задачи (1) – (4) заключается в следующем. Отбрасывается условие целочисленности (4), и полученная ЗЛП (1) – (3) решается симплекс-методом. Если оптимальное решение задачи (1) – (3) удовлетворяет ограничению (4), т.е. является целочисленным, то оно является и решением исходной задачи (1) – (4). Если оптимальное решение задачи (1) – (3) не удовлетворяет ограничению (4), то к основным ограничениям (2) добавляется новое линейное ограничение, обладающее следующими свойствами: 1) оптимальный нецелочисленный план задачи (1) – (3) ему не удовлетворяет; 2) любой целочисленный план задачи (1) – (3) ему удовлетворяет. Затем решается расширенная задача. Процесс повторяется до получения целочисленного решения. Способы построения дополнительного линейного ограничения различны для полностью и частично целочисленных ЗЛП. В силу свойств 1 и 2 дополнительное ограничение называют еще отсечением Гомори, а метод Гомори – методом отсечения.

Рассмотрим метод Гомори для решения полностью целочисленных ЗЛП. Пусть задача (1) – (3) решена симплекс-методом, х⁰ – ее оптимальный план, а табл. 7.1 - оптимальная симплексная таблица.

Таблица 6.1

БП	сБ	А0	хj1	хj2	…	xjn-m	хi1	xi2	…	хim
			сj1	сj2	…	cjn-m	ci1	ci2	…	cim
хi1	ci1	X0i1	ai1j1	ai1j2	…	ai1jn-m	1	0	…	0
хi2	ci2	X0i2	ai2j1	ai2j2	…	ai2jn-m	0	1	…	0
…	…	…	…	…	…	…	…	…	…	…
xim	cim	X0im	aimj1	aimj2	…	aimjn-m	0	0	…	1
zj-cj		f0	zj1-cj1	zj2-cj2	…	zjn-m-cjn-m	0	0	…	0

Если все значения х⁰_ip - целые, то х⁰ – решение задачи (1) – (4). Пусть среди чисел х⁰_ip есть нецелочисленные. Выберем из них число с максимальной дробной частью:

Дополнительное линейное ограничение, или отсечение Гомори, будет иметь вид

(5)

В ограничение (5) вводим дополнительную переменную

(6)

где x_n+10. Равенство (6) умножим на -1 и получим

(7)

Припишем ограничение (7) к симплексной таблице 1. При том переменная x_n+1 будет базисной. Получим расширенную таблицу 2.

Расширенную задачу решают начиная с табл.6.2. Так как в столбце свободных членов табл.6.2 есть отрицательное число, для решения расширенной задачи выполняют следующие операции.

Таблица 6.2

БП	сБ	А0	хj1	хj2	…	xjn-m	хi1	xi2	…	хim	xn+1
			сj1	сj2	…	cjn-m	ci1	ci2	…	cim	0
хi1	ci1	X0i1	ai1j1	ai1j2	…	ai1jn-m	1	0	…	0	0
хi2	ci2	X0i2	ai2j1	ai2j2	…	ai2jn-m	0	1	…	0	0
…	…	…	…	…	…	…	…	…	…	…	…
xim	cim	X0im	aimj1	aimj2	…	aimjn-m	0	0	…	1	0
xn+1	0	-x0ik	-aikj1	-aikj2	…	-aikjn-m	0	0	…	0	1
zj-cj		f0	zj1-cj1	zj2-cj2	…	zjn-m-cjn-m	0	0	…	0	0

1. Просматривают строку, содержащую отрицательное число в столбце свободных членов, и выбирают любое отрицательное число в этой строке. Выбранное число определяет разрешающий столбец.

2. Для чисел с одинаковыми знаками составляют симплексные отношения.

3. Наименьшее симплексное отношение определяет разрешающую строку. На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент.

4. С найденным разрешающим элементом выполняют симплексные преобразования.

Пример. Предприятие производит две модели А и В сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки. Для каждого изделия модели А требуется 2 м² досок, а для изделия В – 5 м². Малое предприятие может получить от своих поставщиков до 1600 м² досок в неделю. Для изготовления каждого изделия модели А требуется 10 мин машинной обработки, а изделие модели В – 12 мин. Время машинной обработки в неделю 100 ч. Сколько изделий каждой модели следует выпускать малому предприятию в неделю для получения максимальной прибыли, если каждое изделие модели А приносит 20 ден. ед. прибыли, а каждое изделие модели В – 40 ден. ед.?

Решение Математическая модель задачи имеет вид

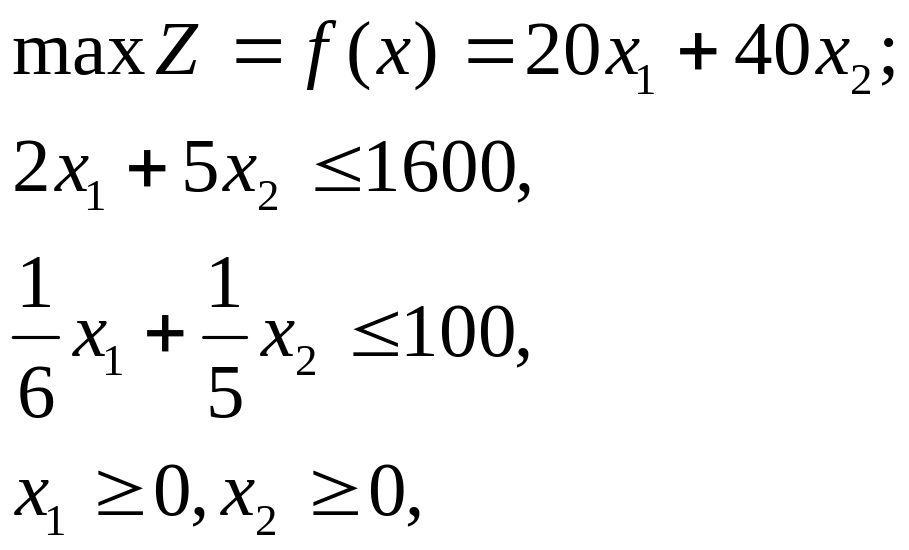
x₁, x₂ – целые.

Преобразуем задачу, умножив обе части второго неравенства на 30. Получим задачу

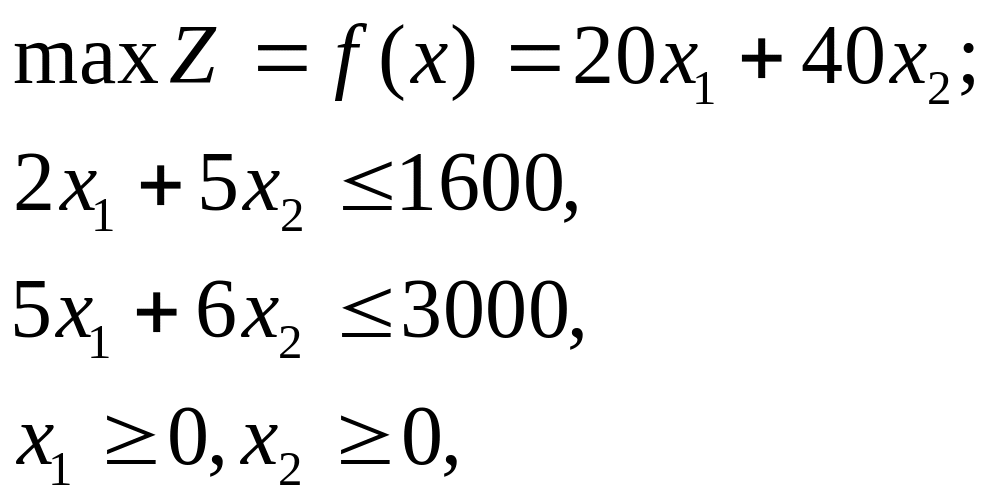
x₁, x₂ – целые.

По методу Гомори для определения оптимального плана задачи ,решим ЗЛП симплекс-методом. Приведем ее к каноническому виду:

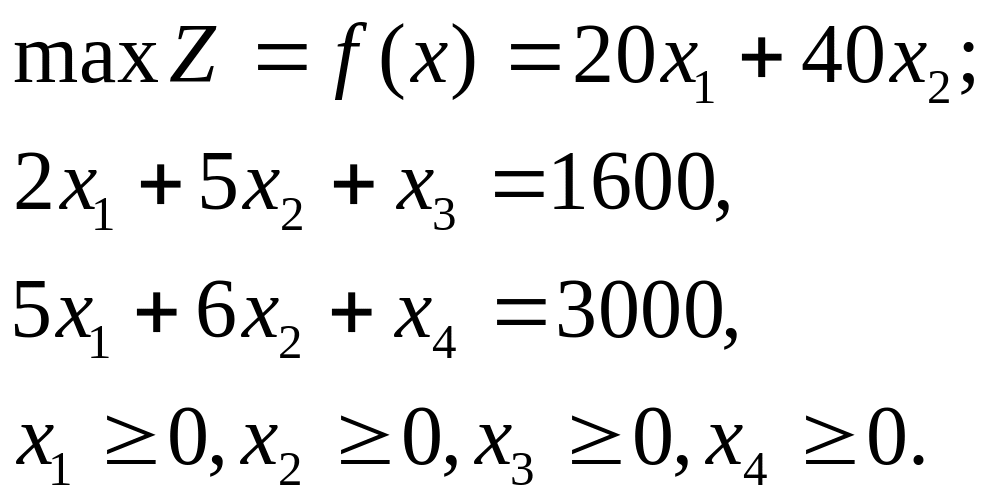
В процессе решения задачи получаются следующие симплекс таблицы

Таблица 6.3

БП	сБ	А0	х1	х2	х3	x4
			20	40	0	0
х3	0	1600	2	5	1	0
х4	0	3000	5	6	0	1
zj-cj		0	-20	-40	0	0

Таблица 6. 4

БП	сБ	А0	х1	х2	х3	x4
			20	40	0	0
х2	40	320	2/5	1	1/5	0
х4	0	1080	13/15	0	-6/5	1
zj-cj		12800	-20/5	0	40/5	0

Таблица 6.5

БП	сБ	А0	х1	х2	х3	x4
			20	40	0	0
х2	40		0	1	5/13	-2/13
х1	20		1	0	-6/13	5/13
zj-cj			0	0	80/13	20/13

Табл.6.5 – оптимальная симплексная таблица,

x⁰=(x⁰₁;x⁰₂), где x⁰₁= , x⁰₂= - оптимальный план задачи. Так как оптимальный план задачи нецелочисленный, он не является оптимальным планом ЗЦЛП. Следуя методу Гомори, находим

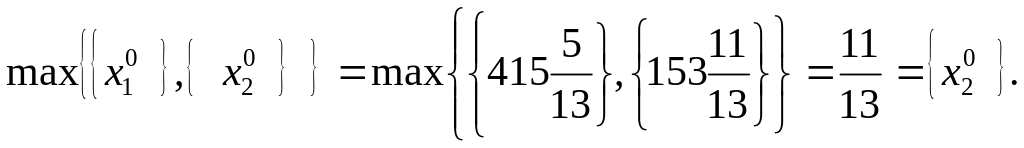По первой строке табл.7.5 строим дополнительное линейное ограничение:

(*)

Так как

ограничение (*) примет вид

Введем в ограничение дополнительную переменную

Домножим ограничение на -1:

Припишем ограничение к табл.7.5 и получим табл.7.6

Таблица 7.6

БП	сБ	А0	х1	х2	х3	x4	x5
			20	40	0	0	0
х2	40		0	1	5/13	-2/13	0
х1	20		1	0	-6/13	5/13	0
x5	0		0	0	-5/13	-11/13	1
zj-cj			0	0	80/13	20/13	0

Следуя методу Гомори, выполним симплексные преобразования табл.6.6 с разрешающим элементом -11/13. Получим табл.6.7.

Таблица 6.7

БП	сБ	А0	х1	х2	х3	x4	x5
			20	40	0	0	0
х2	40
х1	20
x4	0	1
zj-cj			0	0	60/11	0	20/11

Имеем оптимальный целочисленный план расширенной задачи. Тогда оптимальный план исходной задачи х⁰=(415;154).