1.2 Нахождение кратчайших путей между двумя заданными вершинами. Алгоритм Дийкстры

Постановка задачи. Пусть задан ориентированный граф G = (V, E) с заданными положительными длинами ребер l(e)>0, . Нужно найти длину кратчайшего пути (и сам путь), соединяющего две произвольные фиксированные вершины s и t, где s - начало, а t - конец пути.

Для решения данной задачи может быть использован алгоритм Дийкстры (Dijkstra E.W., 1959).

Идея алгоритма состоит в том, что необходимо упорядочить вершины графа по их расстоянию от s. Предположим, что известны m близлежащих к вершине s вершин и известны сами пути, соединяющие эти вершины с s. Как может быть найдена (m + 1)-я близлежащая к s вершина?

Окрасим (пометим) s и m близлежащих к ней вершин. Для каждой неокрашенной вершины u, соседней с одной из окрашенных, построим ребра, соединяющие ее с окрашенными вершинами. После этого выберем кратчайший из путей, соединяющий s с каждой из рассмотренных вершин u. Соответствующая этому кратчайшему пути вершина u является (m + 1)-й близлежащей вершиной.

Таким образом, начиная с вершины s (m = 0) и продолжая процедуру окраски до t, можно построить кратчайший путь от s до t.

Алгоритм Дийкстры

Шаг 1. Вначале алгоритма все вершины не окрашены. Каждой вершине ν во время выполнения алгоритма ставится в соответствие либо число l(ν) — длина кратчайшего пути из s в ν, включающего только окрашенные вершины, либо l’(ν) - временная метка, которая становится равной l(ν) в момент, когда вершина ν окрашивается.

Полагаем: l(s) = 0

l’(ν) = ∞, ν ≠ s

и окрашиваем вершину s.

Шаг 2. Для каждой неокрашенной вершины u, соседней с последней из окрашенных вершин ν, пересчитываем l(u) по формуле:

l(u) = min {l’(u), l(ν) + l(ν,u)},

где l(ν, u) - длина дуги между вершинами ν и u.

Если l’(u) = ∞ для любой неокрашенной вершины u, то алгоритм следует закончить, так как в исходной сети не существует пути из s в неокрашенные вершины, в том числе и в t.

В противном случае находим вершину r, для которой, l’(r) = = min l’(u), после чего вершину r окрашиваем, l(r) = l’(r) и вносим в корневое дерево дугу (ν, r), на которой достигается min в l(r). Вершина r становится последней из окрашенных вершин.

Шаг 3. В момент, когда вершина t становится окрашенной, находим кратчайший путь, соединяющий s и t, состоящий из окрашенных дуг (ребер).

Теорема. Алгоритм Дийкстры строит в графе G = (V, E) кратчайший (s, t) путь.

Пример. Задан граф с фиксированными длинами ребер (рис. 1.4). Найти кратчайший (s, t) путь.

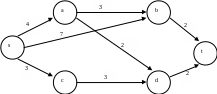
Рис. 1.4

Решение

Шаг 1. l(s) = 0, l’(ν) = ∞, ν ≠ s. Окрашиваем вершину s.

Шаг 2. Производим перерасчет чисел l(u) для неокрашенных вершин u соседних с s.

l’(a) = min {l’(a), l(s) + l(s, a)} = min {∞,0 + 4} = 4,

l’(b) = min {l’(b), l(s) + l(s, b)} = min {∞,0 + 7} = 7,

l’(c) = min {l’(c), l(s) + l(s, c)} = min {∞,0+ 3} = 3.

Таким образом, первой ближайшей к s является вершина c, которую необходимо окрасить (вместе с дугой (s, c)).

Получаем l(c) = 3 (рис. 1.5).

Так как вершина t является неокрашенной, то необходимо снова повторить шаг 2.

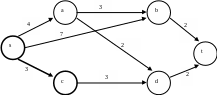
Рис. 1.5

Производим перерасчет меток у вершин, соседних с последней окрашенной вершиной (вершиной с). В данном случае — это единственная вершина d.

l’(d) = min {l’(d), l(c) + l(c, d)} = min {∞,3+3} = 6.

Метки остальных вершин оставляем без изменения:

l’(a) = 4;

l’(b) = 7;

l’(t) = ∞.

Минимум достигается в вершине a.

Окрашиваем вершину a и дугу (s, a), на которой достигается минимум. Вершина a становится последней окрашенной вершиной, l(a) = 4 (рис. 1.6).

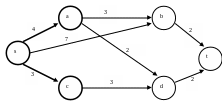
Рис. 1.6

Вершина t по-прежнему не окрашена. Снова повторим шаг 2.

Пересчитываем l(u) у вершин, соседних с a — это вершины b и d.

l’(b) = min {l’(b), l(a) + l(a, b)} = min {7,4+3} = 7,

l’(d) = min {l’(d), l(a) + l(a, d)} = min {6,4+2} = 6,

l’(t) = ∞.

Окрашиваем вершину d. Величину l(d) определяют как дуга (с, d), так и дуга (a, d). Поэтому можно окрасить любую из этих дуг. Например, пусть это будет (c, d), l(d) = 6. Вершина d становится последней из окрашенных вершин (рис. 1.7).

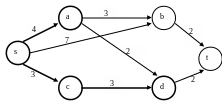
Рис. 1.7

Так как вершина t не окрашена, то переходим снова к шагу 2.

Производим перерасчет меток (это нужно сделать только для вершины t).

l’(t) = min {l’(t), l(d) + l(d, t)} = min {∞,6+2} = 8,

l’(b) = 7. (рис 1.8).

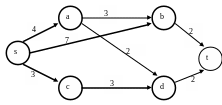
Рис. 1.8

Вершина b становится последней из окрашенных. Т.к. t не окрашена, то повторяем шаг 2.

Производим перерасчет меток (это необходимо сделать только для вершины t, потому что она соседствует с вершиной b).

l’(t) = min {l’(t), l(b) + l(b, t)} = min {8,7+2} = 8.

Окрашиваем вершину t и дугу (d, t) (рис. 1.9).

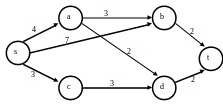
Рис. 1.9

Таким образом, построено дерево кратчайших путей из вершины s, включающее и кратчайший (s, t) - путь (s, t) = {(s, c), (c, d), (d, t)}, длина которого равна 8.

Замечание 1. Данное решение в общем случае не является единственным. Кратчайший путь является единственным только в том случае, если в алгоритме ни разу не возникает однозначности в выборе дуг. В данном примере такая неоднозначность возникла и есть соответствующее альтернативное решение: (s, t) = {(s, a), (a, d), (d, t)}.

Замечание 2. По алгоритму Дийкстры можно находить кратчайшие пути из вершины s во все другие вершины графа. Для этого следует модифицировать в алгоритме только последний шаг.

Если все вершины оказываются окрашенными, то следует закончить алгоритм, иначе перейти к шагу 2.

Замечание 3. Данный алгоритм предполагает неотрицательность длин дуг в заданном графе, и поэтому он не применим к графам, в которых есть отрицательные длины (веса) дуг. Для того чтобы в этом убедиться, достаточно рассмотреть следующий граф (рис. 1.10).

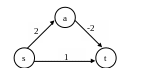
Рис. 1.10

Решая его по алгоритму Дийкстры, получаем, что кратчайший (s, t)-путь есть (s, t) = {(s, t)} и его длина равна 1. В действительности, очевидно, что таким путем является путь {(s, a), (a, t)} с нулевой длиной.