5. Транспортная задача

5.1 Постановка транспортной задачи в матричной форме. Построение исходного опорного плана

Транспортная задача является специальным типом задач ЛП. Экономическая постановка этой задачи следующая. В m пунктах отправления A₁, …, A_m сосредоточен однородный груз в количествах соответственно а₁, …, а_m единиц. Имеющийся груз необходимо доставить потребителям В₁, …, В_n, спрос которых выражается величинами b₁, …, b_n единиц. Известна стоимость с_ij перевозки единицы груза из i-го (i = l, m) пункта отправления в j-й (j = 1, n) пункт назначения. Требуется составить план перевозок, который полностью удовлетворяет спрос потребителей в грузе, и при этом суммарные транспортные издержки минимизируются.

Для построения экономико-математической модели транспортной задачи рассмотрим матрицу

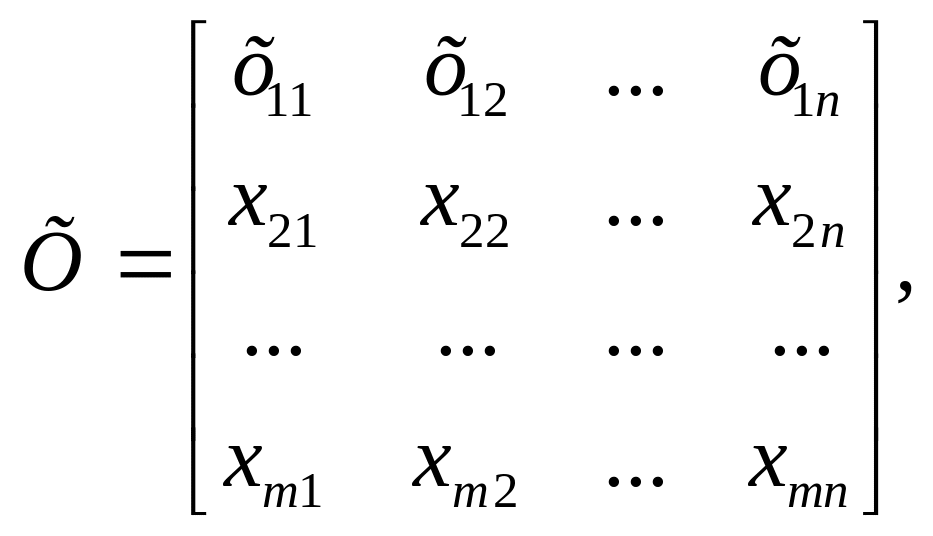
где x_ij (i = 1, m; j = 1, n) обозначает количество единиц груза, которое необходимо доставить из i-гo пункта отправления в j-й пункт назначения.

Матрицу X = [x_ij]_m×n будем называть матрицей перевозок. Предполагается, что все x_ij ≥ 0. Удельные транспортные издержки (расходы) запишем в форме матрицы С = [с_ij]_m×n и назовем ее матрицей тарифов.

Для наглядности условия транспортной задачи можно представить таблицей (табл.5.1), которую будем называть распределительной. Распределительную таблицу называют иногда табличной или матричной моделью транспортной задачи.

Таблица 5.1

Поставщики	Потребители							Запас груза ai
	В1		В2		…	Вn
A1	x11	c11	x12	c12	…	x1n	c1n	a1
А2	x21	c21	x22	c22	…	x2n	c2n	a2
…	…		…		…	…		…
Am	xm1	cm1	xm2	cm2	…	xmn	cmn	am
Потребность в грузе bi	b1		b2		…	bn

Экономико-математическая модель транспортной задачи должна отражать все условия и цель задачи в математической форме. Так, переменные x_ij (i = 1, m; j = 1, n) должны удовлетворять ограничениям по запасам, потребностям и условиям неотрицательности. В математической форме эти условия можно записать так:

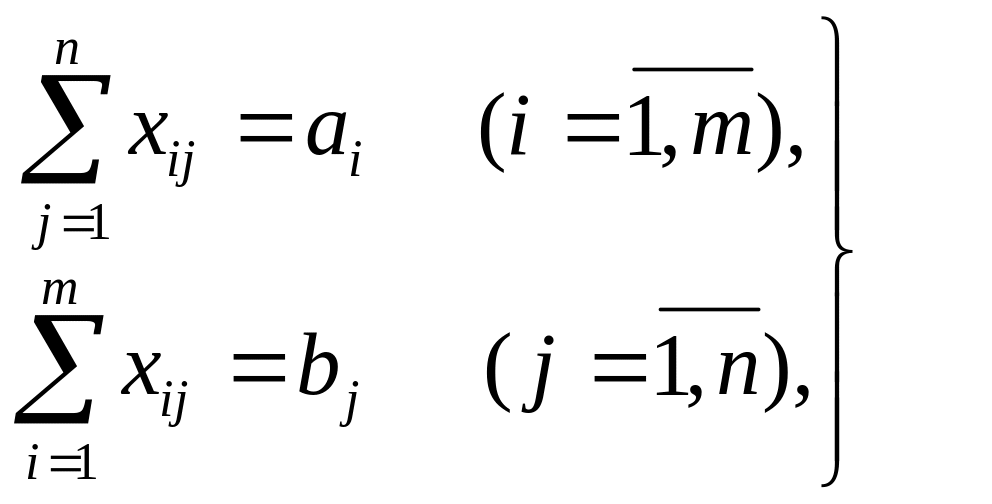(1)

(2)

Цель транспортной задачи — минимизировать общие затраты на реализацию плана перевозок, которые можно представить функцией

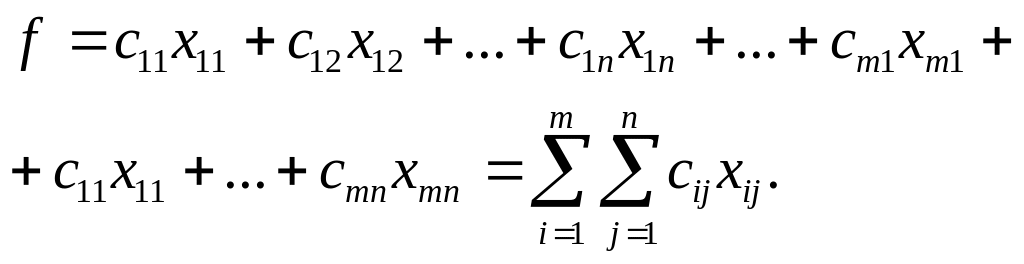(3)

Итак, математически транспортная задача ставится так: Даны система ограничений (1) при условии (2) и линейная функция (3). Требуется среди множества решений системы (1) найти такое неотрицательное решение, при котором линейная функция (3) принимает минимальное значение (минимизируется). [2, с. 144-145]

Будем называть план перевозок X = [x_ij]_m×n допустимым, если он удовлетворяет ограничениям (1) и (2).

Допустимый план перевозок, доставляющий минимум целевой функции (3), называется оптимальным.

Теорема 1 (о существовании допустимого плана). Для того чтобы транспортная задача имела допустимые планы, необходимо и достаточно выполнение равенства

(4)

Доказательство. Просуммировав в распределительной табл. 1 элементы x_ij раздельно по индексам i и j, получим:

Очевидно, что суммируются все элементы x_ij как по строкам, так и по столбцам, различие лишь в перестановке этих элементов. Однако от перестановки слагаемых сумма не меняется. Поэтому равенство

является необходимым условием разрешимости транспортной задачи.

Для доказательства достаточности условия (4) покажем, что если это условие выполняется, то всегда имеется допустимый план. Обозначим

Переменные x_ij выразим через данные задачи следующим образом:

(5)

Поскольку а_i ≥ 0 и bj ≥ 0, то и А > 0, а поэтому и x_ij ≥ (i = l, m; j=1,n).

Покажем, что переменные (5) составляют допустимый план. Этот набор неотрицательных чисел будет составлять допустимый план тогда, когда он удовлетворяет системе ограничений (1). Просуммируем равенства (5) по индексу i. Получим

(6)

Поскольку индекс j не зависит от индекса i, в равенстве (6) вынесем b_j/A за знак суммы и получим

Аналогично, суммируя равенства (5) по индексу j, получаем:

Следовательно, набор чисел x_ij = a_ib_j/A удовлетворяет системе ограничений задачи, а потому является допустимым планом. [2, с. 146]

Модель транспортной задачи называют закрытой, если суммарный объем груза, имеющегося у поставщиков, равен суммарному спросу потребителей, т. е. выполняется равенство:

Если для транспортной задачи выполняется одно из условий:

то модель задачи называют открытой.

Для разрешимости транспортной задачи с открытой моделью необходимо преобразовать ее в закрытую. Так, при выполнении первого условия необходимо ввести фиктивный (n + 1)-й пункт назначения В_n+1, т. е. в матрице задачи предусматривается дополнительный столбец. Спрос фиктивного потребителя полагают равным небалансу, т. е.

а все тарифы — одинаковыми, чаще всего равными нулю, т. е. c_{i, n+1} = 0 (i=l, m).

Аналогично при выполнении второго условия вводится фиктивный поставщик А_{m + 1}, запас груза у которого равен

а тарифы дополнительной строки распределительной таблицы равны нулю, т. е. c_{m + 1, j} = 0 (j=1, n).

При преобразовании открытой задачи в закрытую целевая функция не меняется, так как все слагаемые, соответствующие дополнительным перевозкам, равны нулю.

Теорема 2 (о ранге матрицы). Ранг матрицы А транспортной задачи на единицу меньше числа уравнений: r(A) = m + n - 1.

Доказательство. Матрица системы ограничений (1) имеет вид

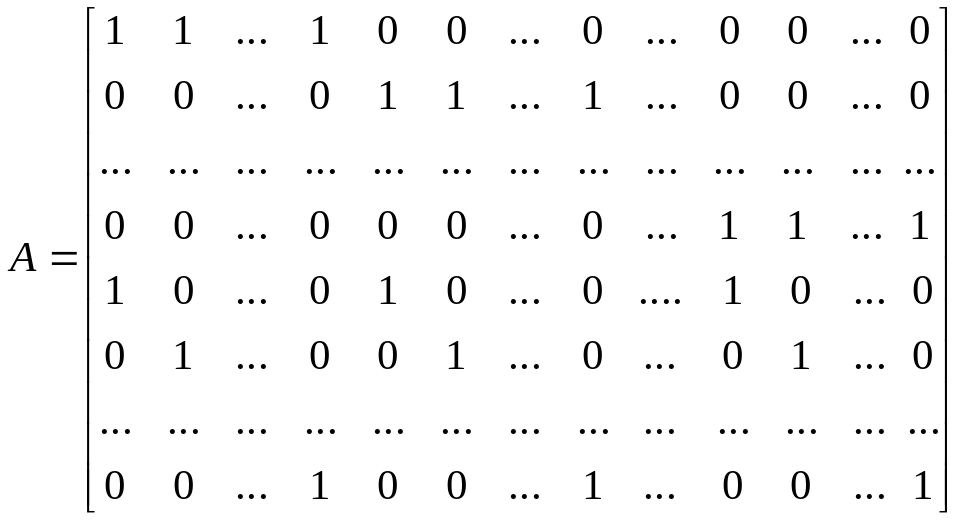
В каждом столбце матрицы А содержатся только два элемента, равных единице, остальные элементы равны нулю. При этом, если сложить первые m строк матрицы, получим строку, элементы которой будут единицы. Этот же результат получаем, если сложить последние n строк. Обозначая i-ю строку через р_i получаем:

p_l + p₂ + ... + p_m = p_m+1 + p_m+2 + ... + p_{m + n}.

Отсюда видно, что любая строка есть линейная комбинация остальных строк.

Значит, не меняя ранга матрицы А, можно вычеркнуть, например, последнюю строку. Минор (m + n - 1)-го порядка получившейся матрицы, составленный из столбцов коэффициентов при x_1n, х_2n, …, x_mn, x₁₁, x₁₂, …, x_{1, n-1} будет отличен от нуля, что и доказывает теорему.

Построение опорных планов будем производить непосредственно в распределительной таблице. Если в плане перевозок переменная х_ik равна некоторому числу а ≠ 0, то это число записываем в соответствующую клетку (i; k) и считаем ее занятой или базисной, если же x_ik = 0, то клетку (i, k) оставляем свободной. При этом число занятых опорным планом клеток в соответствии с теоремой 2 должно быть равно m + n - 1, а остальные mn - (m + n - 1) = (m - 1)(n - 1) клеток будут свободными.

Рассмотрим правило «северо-западного угла». Сущность его состоит в следующем. Пользуясь табл. 1, будем распределять груз, начиная с загрузки левой верхней, условно называемой северо-западной, клетки (1; 1), двигаясь затем от нее по строке вправо или по столбцу вниз. В клетку (1; 1) занесем меньшее из чисел а₁, b₁, т. е. x₁₁ = min (a₁, b₁). Если а₁ > b₁, то x₁₁ = b₁ и первый потребитель В₁ будет полностью удовлетворен. В дальнейшем 1-й столбец таблицы в расчет не принимается; в нем переменные х_i1 = 0 для i = 2, m.

Двигаясь вправо по первой строке таблицы, заносим в соседнюю клетку (1; 2) меньшее из чисел (a₁ – b₁) и b₂, т. е. x₁₂ = min (а₁ – b₁, b₂). Если (а₁ – b₁) < b₂, то запасы первого поставщика исчерпаны и первая строка таблицы в дальнейшем в расчет не принимается. Переходим к аналогичному распределению запаса груза второго поставщика.

Если b₁ > a₁, то x₁₁ = min (a₁, b₁) = а₁. При этом запас первого поставщика будет исчерпан, а потому x_1k = 0 для k = 2, n. Первая строка из дальнейшего рассмотрения исключается. Переходим к распределению запасов второго поставщика. В клетку (2; 1) заносим наименьшее из чисел (а₂, b₁ – а₁).

Заполнив таким образом клетку (1; 2) или (2; 1), переходим к загрузке следующей клетки по второй строке либо по второму столбцу. Процесс распределения по второй, третьей и последующим строкам (столбцам) производится аналогично распределению по первой строке или первому столбцу до тех пор, пока не исчерпаются ресурсы. Последней заполняется клетка (m; n).

Рассмотрим правило «минимального элемента». Сущность его состоит в следующем. Просматриваются тарифы табл. 1 и в первую очередь заполняется клетка с минимальным значением тарифа. При этом в клетку записывается максимально возможное значение поставки. Затем из рассмотрения исключают строку, соответствующую поставщику, запасы которого полностью израсходованы, или столбец, соответствующий потребителю, спрос которого полностью удовлетворен. После этого из оставшихся клеток таблицы снова выбирают клетку с наименьшим тарифом. Процесс распределения заканчивается, когда все запасы поставщиков исчерпаны, а спрос потребителей полностью удовлетворен. В результате получаем опорный план, который должен содержать m + n - 1 загруженных клеток. В процессе заполнения таблицы могут быть одновременно исключены строка и столбец. Так бывает, когда полностью исчерпывается запас груза и полностью удовлетворяется спрос (вырожденная задача). В этом случае в свободные клетки надо записать число 0 — «нуль-загрузка», условно считая такую клетку занятой. Однако число 0 записывается в те свободные клетки, которые не образуют циклов с ранее занятыми клетками.

Рассмотрим метод Фогеля. Сущность его состоит в следующем. В табл. 1 по строкам и столбцам определяется разность между двумя наименьшими тарифами. Отмечается наибольшая разность знаком □. Далее в строке (столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом. Строки (столбцы) с нулевым остатком груза в дальнейшем в расчет не принимаются. На каждом этапе загружается только одна клетка. Распределение груза производится, как и по выше рассмотренным правилам.

Среди полученных опорных планов Х₁ Х₂, Х₃ с различными значениями целевой функции лучшим является Х₃. Будет ли он оптимальным? Чтобы ответить на этот вопрос, необходимо знать признак оптимальности.