
- •1. Теория графов
- •1.1 Остовные деревья минимального веса.
- •Алгоритм Прим
- •Алгоритм Краскал
- •1.2 Нахождение кратчайших путей между двумя заданными вершинами. Алгоритм Дийкстры
- •Алгоритм Дийкстры
- •Модифицированный алгоритм Дийкстры
- •1.3 Нахождение кратчайших цепей между всеми парами узлов в сети
- •Алгоритм Флойда (Floyd r. W.)
- •Модификация алгоритма Флойда
- •1.4 Построение потоков максимальной мощности. Алгоритм Форда-Фалкерсона
- •Алгоритм Форда-Фалкерсона
- •1.5 Обобщенные задачи о потоке
- •1.5.1 Построение потока в сети с двойным ограничением потока по дугам
- •1.5.2 Построение потока в сети с пропускными способностями узлов
- •1.5.3 Построение потока в сети с несколькими источниками-стоками
- •1.5.4 Построение потока в сети с неориентированными ребрами
- •1.6 Определение потока заданной величины минимальной стоимости. Алгоритмы Басакера-Гоуэна, Клейна
- •Алгоритм Басакера-Гоуэна (Basaker r.G., Gowen p.J)
- •Алгоритм Клейна (Klein m.)
- •2 Сетевое планирование
- •2.1 Построение сетевых моделей
- •2.2 Расчет и анализ сетевых моделей
- •Задача №1
- •Задача №2
- •I. Поиск критических путей
- •II. Поиск резервов работ
- •Правило №2.1
- •3 Линейное программирование
- •3.1 Примеры задач лп
- •3.2 Свойства решений задач линейного программирования
- •3.3 Двумерные задачи линейного программирования. Графический метод решения. Исследование на разрешимость
- •3.3.1 Построение области допустимых решений целевой функции f.
- •3.3.2 Построение прямой уровня
- •3.3.3 Максимизация целевой функции f
- •3.4 Симплекс-метод.
- •3.4.1 Построение начального опорного плана.
- •3.4.2 Симплексные таблицы
- •3.4.3 Примеры решения задач симплекс-методом
- •4. Теория двойственности в линейном программировании
- •4.1 Понятие двойственности. Построение пары взаимно двойственных задач
- •4.2 Теоремы двойственности и их экономическое содержание
- •4.3 Анализ решения задач линейного программирования
- •5. Транспортная задача
- •5.1 Постановка транспортной задачи в матричной форме. Построение исходного опорного плана
- •5.2 Метод потенциалов
- •5.3 Дополнительные условия в транспортных задачах.
- •6. Дискретное программирование.
- •6.1 Метод Гомори для решения задачи целочисленного линейного программирования
- •7. Динамическое программирование
- •7.1 Многошаговые процессы в динамических задачах
- •7.2 Принцип оптимальности и рекуррентные соотношения
- •7.3 Вычислительная схема динамического программирования
- •7.4 Оптимальное распределение средств на расширение производства
- •8. Матричные игры
- •8.1 Парные матричные игры с нулевой суммой
- •8.2 Платежная матрица
- •Нижняя и верхняя цена игры
- •8.3 Смешанные стратегии
- •8.3 Решение матричной игры сведением к задаче линейного программирования
- •8.4 Решение матричной игры графическим методом
- •8.5 Приближенный метод решения матричных игр
- •Практические работы Практическая работа №1 Построение остовного дерева графа. Нахождение найкратчайшего расстояния между заданными вершинами графа
- •Практическая работа №2 Нахождение наикратчайших расстояний между всеми парами вершин графа. Алгоритм Флойда.
- •Практическая работа №3
- •Практическая работа №4 Нахождение потока заданной величины минимальной стоимости. Алгоритм Басакера-Гоуэна
- •Практическая работа №7 Оптимизация проекта по времени.
- •Практическая работа №8
- •Практическая работа №9 Оптимизация целевой функции с помощью двухфазного симплекс метода.
- •Практическая работа №10 Решение двойственных задач. Экономическая интерпретация задач линейного программирования.
- •Практическая работа №11 Решение транспортных задач.
- •Практическая работа №12 Дополнительные условия в транспортных задачах
- •Практическая работа №13 Метод Гомори для решения задачи целочисленного линейного программирования.
- •Практическая работа №14
- •Практическая работа №15 Решение матричных игр в чистых стратегиях
- •Практическая работа №16 Графический метод решения матричных игр.
- •Каркас минимального веса. Метод р. Прима.
- •Кратчайшие пути
- •Лабораторная работа №2 Кратчайшее расстояния от заданной вершины до всех остальных вершин графа.
- •Алгоритм Дийкстры.
- •Пути в бесконтурном графе.
- •Лабораторная работа №3 Кратчайшие пути между всеми парами вершин графа.
- •Алгоритм Флойда.
- •Лабораторная работа №4 Построение потока максимальной мощности.
- •Потоки в сетях.
- •Метод построения максимального потока в сети.
- •Лабораторная работа №5 Симплекс метод
- •Лабораторная работа №6 Транспортная задача
- •Список литературы
1.5 Обобщенные задачи о потоке
Рассмотрим некоторые обобщения задачи о нахождении максимального потока заданной сети, которые также могут быть решены с помощью рассматриваемого базового алгоритма Форда-Фалкерсона.
1.5.1 Построение потока в сети с двойным ограничением потока по дугам
В данной задаче наряду с рассмотренными условиями выполняется ещё одно дополнительное условие:
![]() для
любой дуги
.
для
любой дуги
.
Очевидно,
что в данной ситуации уменьшение потока
на обратных дугах будет ограничено
нижней границей
![]() для
потока на рассматриваемой дуге.
для
потока на рассматриваемой дуге.
Упражнения
Определить допустимый поток в данной модифицированной сети и привести формулировку задачи о нахождении максимального потока. Сформулировать условия существования допустимого потока.
Модифицировать алгоритм Форда-Фалкерсона для построения максимального потока в сети с двойным ограничением потока по дугам.
1.5.2 Построение потока в сети с пропускными способностями узлов
Такой
сетью является сеть, в которой узлы
(вершины) могут также обладать пропускной
способностью, т.е. когда дополнительно
заданы числа c(x)
для некоторых
![]() .
Для того, чтобы свести данную задачу к
базовой, необходимо представить, что
каждая вершина x, обладающая пропускной
способностью, «растягивается» в
дополнительную дугу (x1,
x2), которой
присваивается пропускная способность
вершины x,
т.е.
.
Для того, чтобы свести данную задачу к
базовой, необходимо представить, что
каждая вершина x, обладающая пропускной
способностью, «растягивается» в
дополнительную дугу (x1,
x2), которой
присваивается пропускная способность
вершины x,
т.е.
![]() .
.
Упражнения
Определить допустимый поток в данной модифицированной сети и привести формулировку задачи о нахождении максимального потока.
Модифицировать алгоритм Форда-Фалкерсона
Для построения максимального потока в сети с пропускными способностями узлов.
1.5.3 Построение потока в сети с несколькими источниками-стоками
Данная модификация предполагает, что в сети заданы n источников s1, s2, …, sn и m стоков t1, t2, …, tm.
Чтобы свести данную задачу к базовой, вводят в рассмотрение фиктивные источники – главный источник S и главный сток T, а также фиктивные дуги (S, s1), …, (S, sn) и (t1, T), …, (tm, T) и полагают пропускную способность дуг, выходящих из S и соответственно входящих в T, равной .
1.5.4 Построение потока в сети с неориентированными ребрами
В данной модификации предполагается, что в сети имеются ребра, т.е. дуги без заданной ориентации, но с заданными пропускными способностями. Для приведения данной сети к базовой каждое ребро заменяется на две дуги противоположной ориентации, но с теми же вершинами и пропускной способностью, равной пропускной способности ребра.
Упражнения
Определить допустимый поток в данной модифицированной сети и привести формулировку задачи о нахождении максимального потока.
Модифицировать алгоритм Форда-Фалкерсона для построения максимального потока в сети с неориентированными ребрами.
1.6 Определение потока заданной величины минимальной стоимости. Алгоритмы Басакера-Гоуэна, Клейна
В
предыдущем разделе рассматривалась
сеть
![]() ,
каждой дуге (x, y) которой соответствовала
пропускная способность дуги
,
каждой дуге (x, y) которой соответствовала
пропускная способность дуги
![]() ,
указывающая максимальное количество
потока, которое по ней можно пропустить.
,
указывающая максимальное количество
потока, которое по ней можно пропустить.
Для
данной задачи нахождения потока заданной
величины минимальной стоимости
необходимо, каждой дуге
![]() было
поставлено в соответствие неотрицательное
действительное число
было
поставлено в соответствие неотрицательное
действительное число
![]() ,
называемое стоимостью доставки единицы
потока по дуге
.
Если в сети пропущен поток f, то стоимостью
потока называется число
,
называемое стоимостью доставки единицы
потока по дуге
.
Если в сети пропущен поток f, то стоимостью
потока называется число
![]() .
.
Постановка
задачи. Пусть
—
сеть с заданными пропускными способностями
,
![]() и стоимостями
и стоимостями
![]() ,
дуг. Среди допустимых потоков (т.е.
потоков, удовлетворяющих условиям
,
дуг. Среди допустимых потоков (т.е.
потоков, удовлетворяющих условиям
![]() )
заданной мощности
)
заданной мощности
![]() ,
найти поток минимальной стоимости
,
найти поток минимальной стоимости
![]() .
.
При этом подразумевается, что величина не превышает максимальной мощности допустимого потока из s в t, иначе задача не имеет решения.
В
излагаемых далее алгоритмах построения
потока минимальной стоимости существенную
роль играет так называемый граф
модифицированных стоимостей
![]() .
.
Пусть
дан граф
,
в котором пропущен допустимый поток f.
Граф
![]() строится
следующим образом: множество вершин
совпадает с множеством вершин графа G,
т.е.
строится
следующим образом: множество вершин
совпадает с множеством вершин графа G,
т.е.
![]() ;
множество
;
множество
![]() определяется
правилами:
определяется
правилами:
Если и
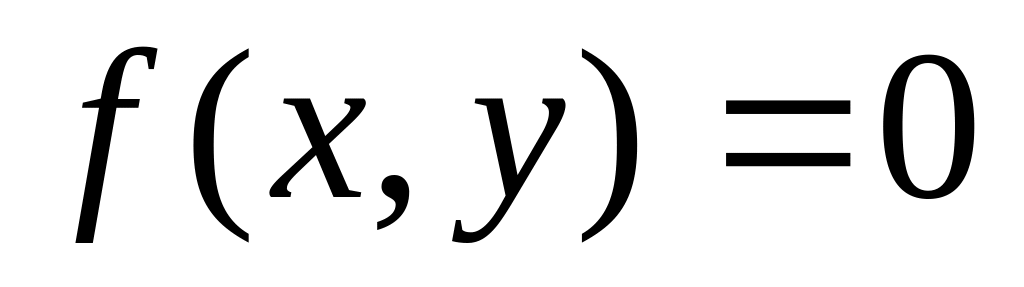 ,
то в графе
рисуется
одна дуга
,
то в графе
рисуется
одна дуга
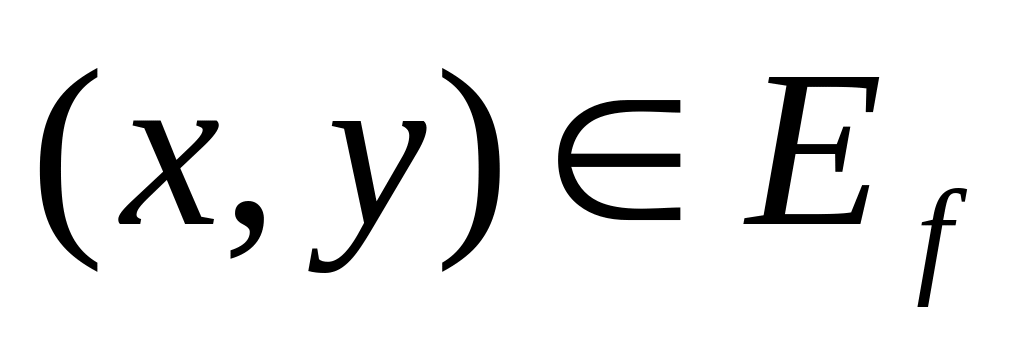 ,
имеющая длину (модифицированную
стоимость)
,
имеющая длину (модифицированную
стоимость)
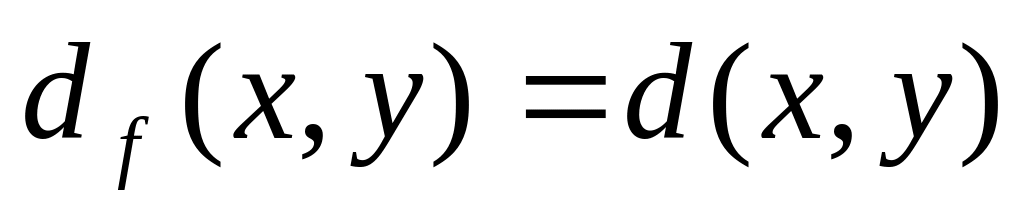 .
.Если и
 ,
то в графе
рисуется
одна дуга
,
то в графе
рисуется
одна дуга
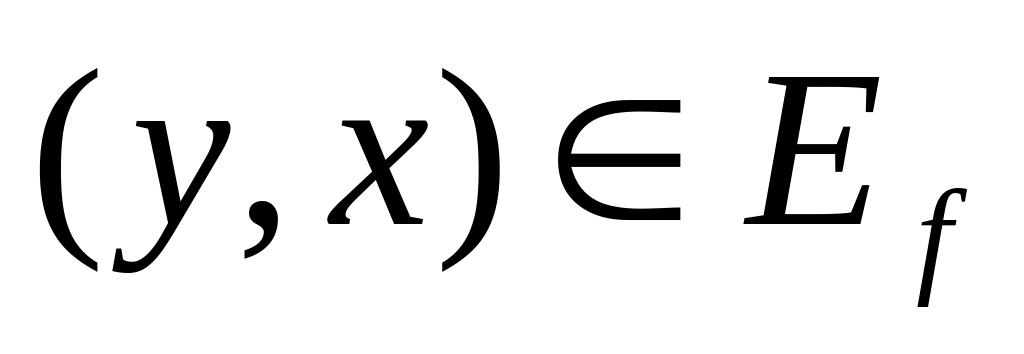 ,
имеющая длину (модифицированную
стоимость)
,
имеющая длину (модифицированную
стоимость)
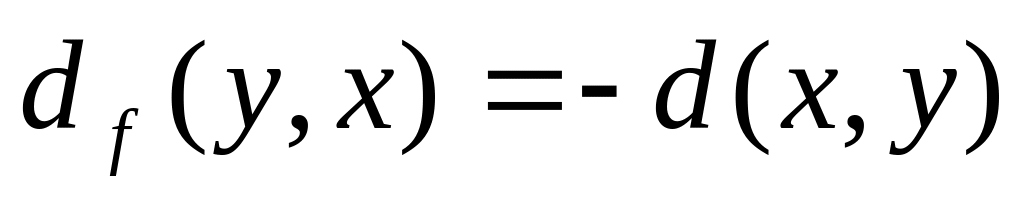 .
.Если и
 ,
то в графе
рисуется две дуги
и имеющие соответственно длины
и
,
то в графе
рисуется две дуги
и имеющие соответственно длины
и
Пример. Пусть задан граф , в котором пропущен допустимый поток f (см. Рис.1.22).
В
данном графе над каждой дугой
числа
![]() показывают
соответственно пропускную способность,
пропущенный по дуге поток и стоимость
единицы потока. Тогда граф
имеет
вид (см. Рис. 1.23)
показывают
соответственно пропускную способность,
пропущенный по дуге поток и стоимость
единицы потока. Тогда граф
имеет
вид (см. Рис. 1.23)
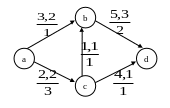
Рис. 1.22
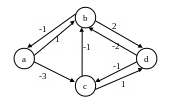
Рис. 1.23
