3.4.2 Симплексные таблицы
Приведя модель ЗЛП к предпочтительному виду, ее заносят в так называемую симплексную таблицу.
Таблица 4.1
БП |
сБ |
А0 |
х1 |
х2 |
… |
xi |
… |
хm |
xm+1 |
… |
xj |
… |
хn |
с1 |
с2 |
… |
ci |
… |
cm |
cm+1 |
… |
cj |
… |
cn |
|||
х1 |
c1 |
b1 |
1 |
0 |
… |
0 |
… |
0 |
a1,m+1 |
… |
a1j |
… |
a1n |
х2 |
c2 |
b2 |
0 |
1 |
… |
0 |
… |
0 |
a2,m+1 |
… |
a2j |
… |
a2n |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
xi |
ci |
bi |
0 |
0 |
… |
1 |
… |
0 |
ai,m+1 |
… |
aij |
… |
ain |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
хm |
cm |
bm |
0 |
0 |
… |
0 |
… |
1 |
am,m+k |
… |
amj |
… |
amn |
zj-cj |
∆0 |
0 |
0 |
… |
0 |
… |
0 |
∆m+1 |
… |
∆i |
… |
∆n |
|
Рабочая часть таблицы, начиная с 3-го столбца и 3-й строки, содержит элементы расширенной матрицы, над которыми будут производиться преобразования с целью получения оптимального плана. В последней строке (zj-cj) таблицы записано «нулевое» уравнение (целевая функция Z). Эта строка называется уравнение индексной или строкой оценок. В столбец БП занесены базисные (предпочтительные) переменные. Столбец сБ содержит коэффициенты целевой функции, стоящие при базисных переменных. Столбец А0 содержит свободные члены bi 0 системы ограничений. Сверху над рабочей частью таблицы указаны все переменные и коэффициенты целевой функции cj.
Остановимся на заполнении индексной строки zj-cj. Здесь расположены значение целевой функции для
начального опорного плана х0 ,т. е. z(х0) = 0 = сБ A0, и оценки индексной строки j = сБ Aj – cj.
Проиллюстрируем процесс заполнения таблицы на примере следующей задачи:
Пример.
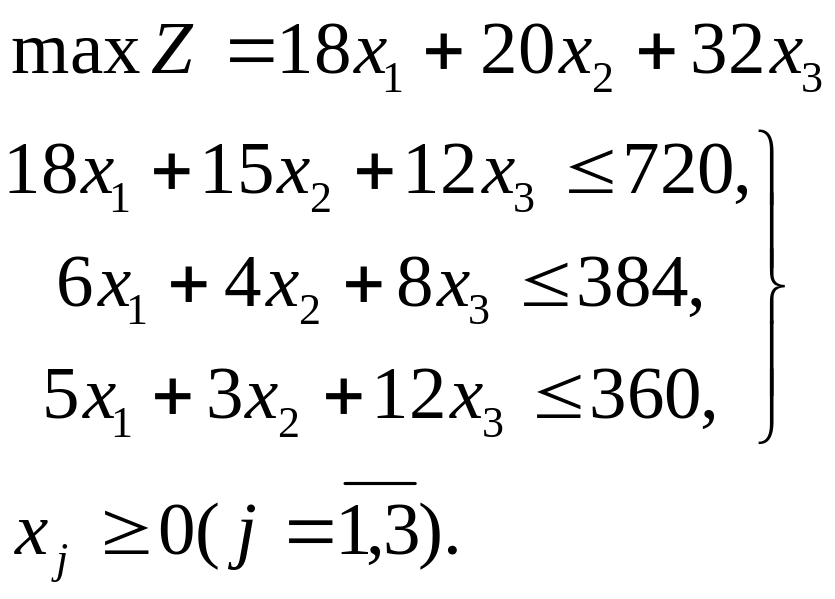
Решение Введя дополнительные переменные х4, х5 и х6, придем к канонической форме:
.
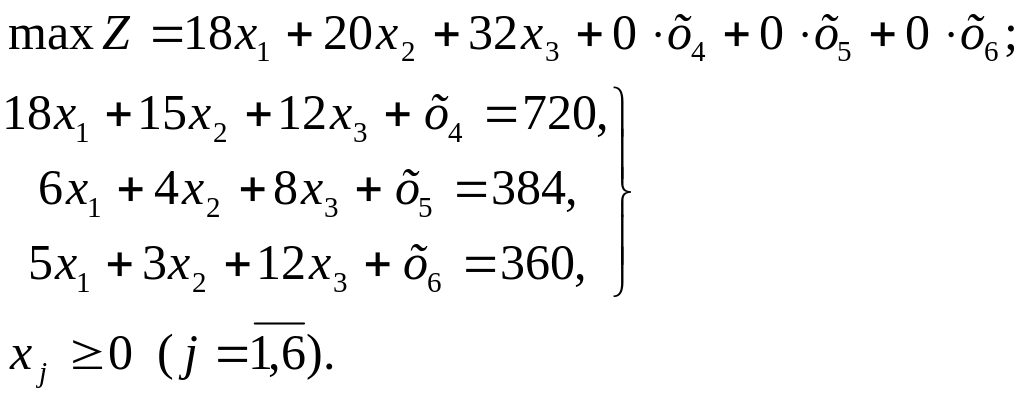
Заносим условия задачи в симплексную таблицу
Таблица 4.2
БП |
сБ |
А0 |
х1 |
х2 |
x3 |
х4 |
x5 |
x6 |
18 |
20 |
32 |
0 |
0 |
0 |
|||
х4 |
0 |
720 |
18 |
15 |
12 |
1 |
0 |
0 |
х5 |
0 |
384 |
6 |
4 |
8 |
0 |
1 |
0 |
x6 |
0 |
360 |
5 |
3 |
12 |
0 |
0 |
1 |
zj-cj |
0 |
-18 |
-20 |
-32 |
0 |
0 |
0 |
|
Индексная строка zj-cj заполнена по известным формулам 0 = сБ A0, j = сБ Aj – cj:
0 = 0 720 + 0 384 + 0 360 = 0
1 = 0 18 + 0 6 + 0 5 – 18 = -18
2 = 0 15 + 0 4 + 0 3 - 20 = -20
3 = 0 12 + 0 8 + 0 12 - 32 = -32
4 = 0 1 + 0 0 + 0 0 - 0 = 0
5 = 0 0 + 0 1 + 0 0 - 0 = 0
6 = 0 0 + 0 0 + 0 1 - 0 = 0.
Приравнивая
х1,
х2 и
х3
нулю, находим х4
= 720,
х5
= 384,
х6
= 360 и тем самым начальный опорный план
В столбце
A0
индексной строки получено значение 0
= 0 целевой
функции, соответствующее плану х0.
Признак оптимальности опорного плана задачи максимизации: если для некоторого опорного плана все оценки j неотрицательны, то такой план оптимален; если же исходная задача на минимум и j неположительны, то такой план оптимален.
Так, содержащийся в табл. опорный план не является оптимальным, поскольку 1 = -18, 2 = -20, 3 = -32.
Рассмотрим переход к нехудшему опорному плану на примере ЗЛП на максимум. Приведем ее к каноническому виду и занесем в симплексную таблицу. Если все j 0, то начальный опорный план х0 оптимален. Если же существуют j < 0, то план неоптимален, при определенных условиях его можно улучшить. Среди отрицательных оценок находят максимальную по абсолютной величине:
Столбец j0 называется разрешающим. Если задача решается на минимум, то разрешающий столбец выбирается из условия
Переменную
,
соответствующую разрешающему столбцу,
следует ввести в базис. Для определения
переменной, выводимой из базиса, находят
отношения
(они называются симплексными). Среди симплексных отношений определяют наименьшее, т. е.
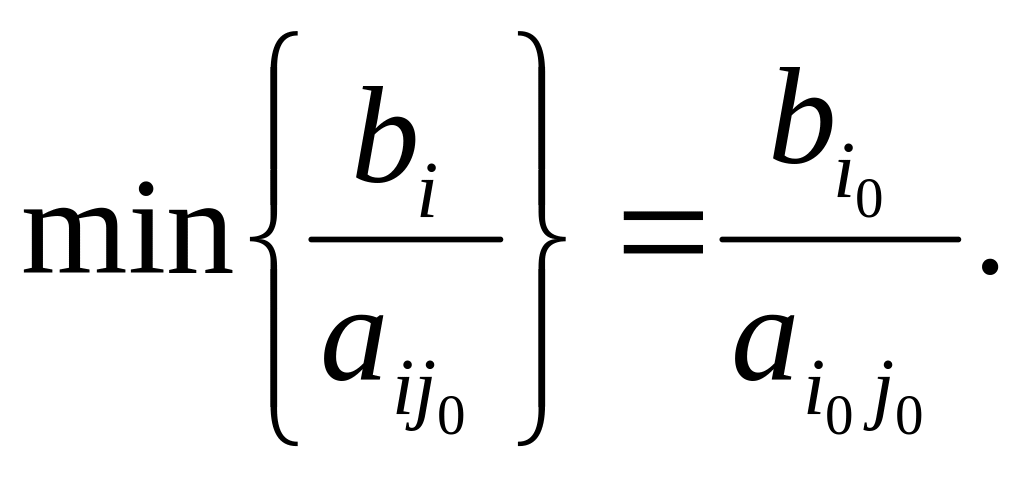
Оно и укажет строку, в которой содержится исключаемая из базиса переменная . Строка i0, соответствующая минимальному симплексному отношению, называется разрешающей. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки, также называется разрешающим. Чтобы завершить шаг преобразований, ведущих к новому опорному плану, составляют таблицу по следующим правилам:
элементы строки i0 новой таблицы равны соответствующим элементам разрешающей строки старой таблицы, деленным на разрешающий элемент;
все элементы столбца j0 новой таблицы равны нулю, за исключением
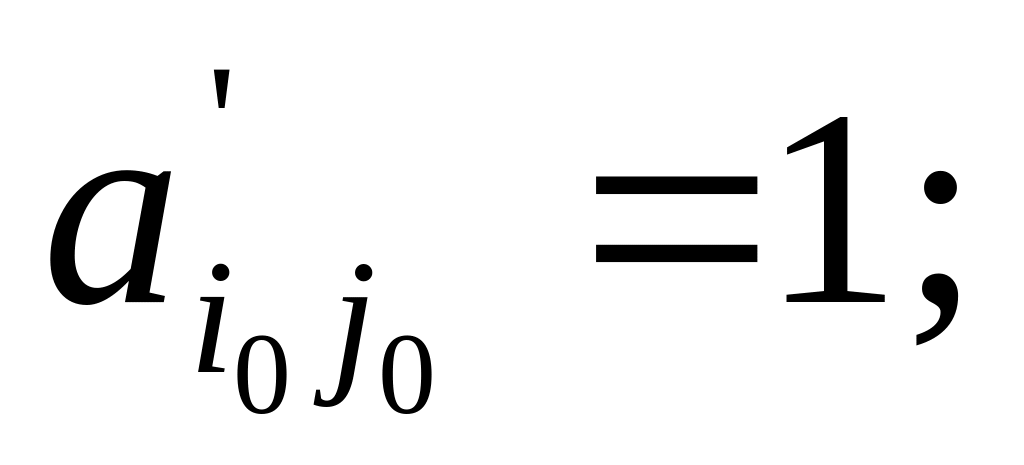
чтобы получить все остальные элементы (включая элементы индексной строки) новой таблицы, надо из соответствующего элемента прежней таблицы вычесть произведение элемента разрешающей строки на элемент разрешающего столбца, разделенное на разрешающий элемент.
Для контроля вычислений элементов индексной строки применяют формулы:
0 = сБ A0, j = сБ Aj – cj:
Альтернативный оптимум (признак бесконечности множества оптимальных планов): если в индексной строке последней симплексной таблицы (содержащей оптимальный план) имеется хотя бы одна нулевая оценка, соответствующая свободной переменной (небазисные переменные), то задача ЛП имеет бесконечное множество оптимальных планов.
Признак неограниченности целевой функции: если в разрешающем столбце нет ни одного положительного элемента, то целевая функция на множестве допустимых планов не ограничена.
Признак несовместимости системы ограничений: если в оптимальном плане М- задачи не все искусственные переменные равны нулю, то система ограничений исходной задачи несовместна.