Правило №2.1

Полный резерв любой работы складывается из собственного свободного резерва и минимального из полных резервов непосредственно следующих работ.

За работой (4,6) следует только критическая работа (6,7) с нулевым полным резервом. Поэтому .

4)     Работа (4,5) заканчивается в 12-й день, в этот же день начинается следующая работа (5,7), т.е. любая задержка выполнения работы (4,5) приведет к задержке начала работы (5,7). Это означает, что работа (4,5) не имеет свободного резерва . Но если сдвинуть во времени работу (4,5) на 1 день, то работа (5,7) также сдвинется на 1 день и это не нарушит срок выполнения проекта, т.к. у работы (5,7) есть временной резерв. Таким образом согласно правилу №2.1

5)     Работа (1,5) заканчивается в 10-й день, в то время как последующая работа (5,7) начинается в 12-й день. Т.е. работа (1,5) может задержаться на 2 дня и это никак не повлияет на время начала последующей работы (5,7), т.е. . Кроме того, поскольку последующая работа (5,7) имеет резерв в 1 день, то, в общем, работу (1,5) можно сдвинуть на 3 дня и это не нарушит сроков проекта (см. рис.2.4), т.е.

6)     Работа (1,4) заканчивается во 2-й день, и в этот же день начинаются следущие работы (4,5) и (4,6). Т.е. работа (1,4) не имеет свободного резерва времени . Поскольку после работы (1,4) следуют две работы с различными полными резервами, то согласно правилу №2.1

7) Работа (1,3) заканчивается в 3-й день, а следующие за ней работы (3,6) и (3,7) начинаются в 5-й день, т.е. . Поскольку обе последующие работы критические, то полный и свободный резерв работы (1,3) совпадают

8. Ненулевые свободные резервы работ обозначены на графике привязки фигурными скобками (см. рис.2.11).

3 Линейное программирование

3.1 Примеры задач лп

Линейное программирование - это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.

Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.

Математическая модель любой задачи линейного программирования включает в себя:

1) максимум или минимум целевой функции (критерий оптимальности);

2) систему ограничений в форме линейных уравнений и неравенств;

3) требование неотрицательности переменных.

Рассмотрим алгоритм составления математической модели задачи на примере.

Пример 1. Фирма производит две модели А и В сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки. Для каждого изделия модели А требуется 3 м² досок, а для модели В - 4 м². Фирма может получать от своих поставщиков до 1700 м² досок в неделю. Для каждого изделия модели А требуется 12 мин. машинного времени, а для изделия модели В - 30 мин. В неделю можно использовать 160 часов машинного времени.

Сколько изделий каждой модели следует выпускать фирме в неделю, если каждое изделие модели А приносит 2 дол. прибыли, а каждое изделие модели В - 4 дол. прибыли?

Сведем все данные в табл.

Таблица 3.1

Ресурс	Модели книжных полок		Запас ресурсов
	А	Б
Доски, м2	3	4	1700
Машинное время, мин	12	30	150
Цена	2	4

Построение математической модели.

Пусть х₁ - количество выпущенных за неделю полок модели А,

х₂ - количество выпущенных полок модели В.

Тогда: 3x₁ - количество досок требуемых на неделю для изготовления полок модели А,

4х₂- количество досок требуемых на неделю для изготовления полок модели В.

3x₁ + 4х₂ - количество досок требуемых на неделю для изготовления книжных полок двух моделей, а по условию задачи это число не должно превышать 1700 м². Следовательно, получаем первое ограничение:

3x₁ + 4х₂ ≤ 1700 (1)

Найдем ограничение на использование машинного времени:

12 мин. составляют 0,2 часа, а 30 мин. - 0,5 часа.

Таким образом: 0,2x₁ - количество времени, требуемое на неделю для обработки полок модели А;

0,5х₂ - количество времени, требуемое на неделю для обработки полок модели В;

0,2x₁ + 0,5х₂ - количество времени, требуемое на неделю для обработки двух моделей, а по условию задачи это число не должно превышать 160 часов. Следовательно, получаем второе ограничение:

0,2x₁ + 0,5х₂ ≤ 160 или 2x₁ + 5х₂ ≤ 1600 (2)

Кроме того, поскольку x1 и х2 выражают еженедельный объем выпускаемых изделий, то они не могут быть отрицательными, то есть

x₁ ≥ 0, х₂ ≥0 (3)

Наша задача состоит в том, чтобы найти такие значения x₁ и х₂, при которых еженедельная прибыль будет максимальной.

Составим выражение для еженедельной прибыли:

2x₁ - еженедельная прибыль, получаемая от продажи полок модели А.

4х₂ - еженедельная прибыль, получаемая от продажи полок модели В.

F=2x₁ + 4х₂ - еженедельная прибыль, которая должна быть максимальной.

Таким образом, имеем следующую математическую модель для данной задачи.

F=2x₁ + 4х₂ → max

Полученная модель является задачей линейного программирования. Функция F это целевая функция, она является линейной функцией своих переменных (x₁, х₂). Ограничения на эти переменные (1) и (2) тоже являются линейными. Выполнено условие неотрицательности для переменных x₁ и х₂.

Необходимо найти значения переменных x₁ и х₂, при которых данная функция F принимает максимальное значение, при соблюдении ограничений, накладываемых на эти переменные.

Решения, удовлетворяющие системе ограничений и требованием неотрицательности, являются допустимыми, а решения, удовлетворяющие одновременно и требованием минимизации (максимизации) функции в целом являются оптимальными.

Задача математического программирования называется задачей линейного программирования, если целевая функция f есть линейная функция, а множество допустимых решений х задается с помощью линейных неравенств или линейных уравнений.

В общем виде задачу линейного программирования можно представить в следующем образом.

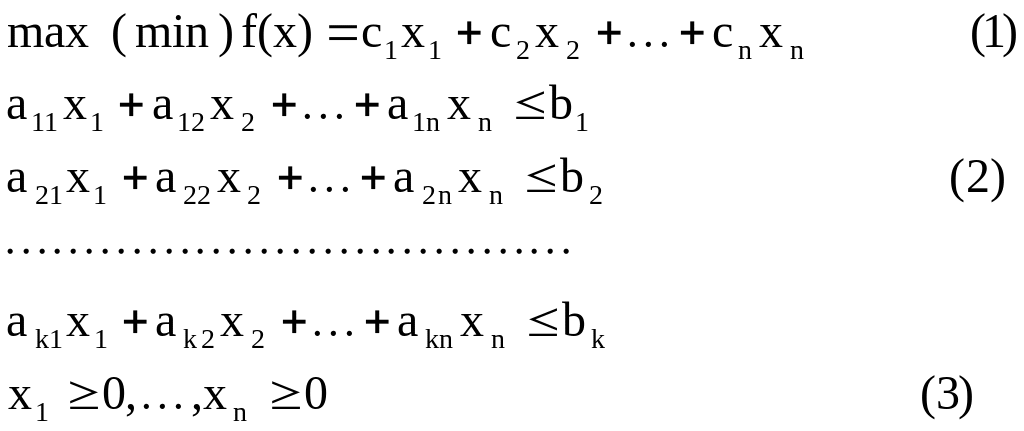
(l)-(3) - это стандартная постановка задачи ЛП (в общем случае в ограничениях (2) могут быть различные соотношения вида «≤», «≥», «=»).

с₁,…, c_n - коэффициенты при целевой функции,

а₁₁, …, а_kn - коэффициенты при ограничениях,

b₁, …, b_k - свободные члены при ограничениях.

Все они являются известными числами (заданы).

Неизвестными являются переменные х₁, …, х_n.

В задачах (1) - (3) требуется найти такие значения переменных (точку максимума), чтобы:

1. эти переменные удовлетворяли всем ограничениям (2) и (3) (условие допустимости);

2. В точке х* = ( ) целевая функция f принимала максимальное значение f(x*) (условие оптимальности).

Аналогично ставится задача на минимум.