3.4 Симплекс-метод.

Существует универсальный способ решения задач ЛП, называемый симплекс-методом.

Идея симплекс-метода. Сначала надо найти некоторую (начальную) вершину многогранника допустимых решений (начальный опорный план). Затем надо проверить это решение на оптимальность. Если оно оптимально, то решение найдено; если нет, то перейти к другой вершине многогранника и вновь проверить на оптимальность. Надо заметить, что при переходе от одной вершины к другой значение целевой функции убывает (в задаче на минимум) или возрастает (в задаче на максимум).

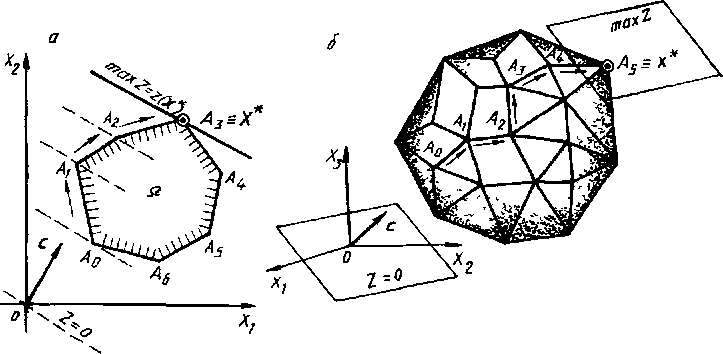
рис.4.1

3.4.1 Построение начального опорного плана.

Рассмотрим три случая.

1-й случай. Пусть в системе ограничений имеется единичный неотрицательный базис. Например, она имеет вид

Говорят, что ограничение канонической ЗЛП имеет предпочтительный вид, если при неотрицательности его правой части (b_i  0) левая часть содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения – с коэффициентом равным нулю. Если каждое ограничение канонической ЗЛП имеет предпочтительный вид, т. е. система ограничений приведена к единичному неотрицательному базису, то начальный опорный план строится весьма просто. Предпочтительные переменные выбираются в качестве базисных, а все остальные – свободные. Свободные переменные приравниваются нулю, а базисные переменные – свободным членам.

Пример. Найти начальный опорный план ЗЛП

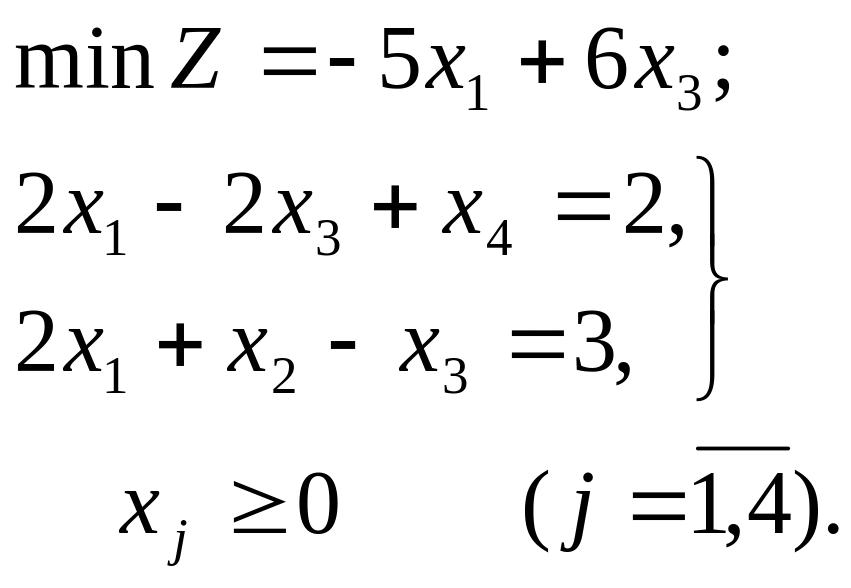
Решение В первом ограничении предпочтительной переменной является х₄, во втором – х₂. Система приведена к положительному единичному базису. Свободные переменные х₁ и х₃ приравниваются нулю. Получим невырожденный начальный опорный план:

х₀ = (0; 3; 0; 2); Z(x₀) = 0.

2-й случай. Пусть система ограничений имеет вид

Сведем задачу к каноническому виду, добавив к левым частям системы ограничений дополнительные переменные х_n+i  0 (i=1…m).

Получим систему ограничений

эквивалентную исходной и имеющую предпочтительный вид. Отсюда получаем начальный опорный план:

В целевую функцию дополнительные переменные вводятся с коэффициентами, равными нулю:

Пример. Найти начальный опорный план ЗЛП

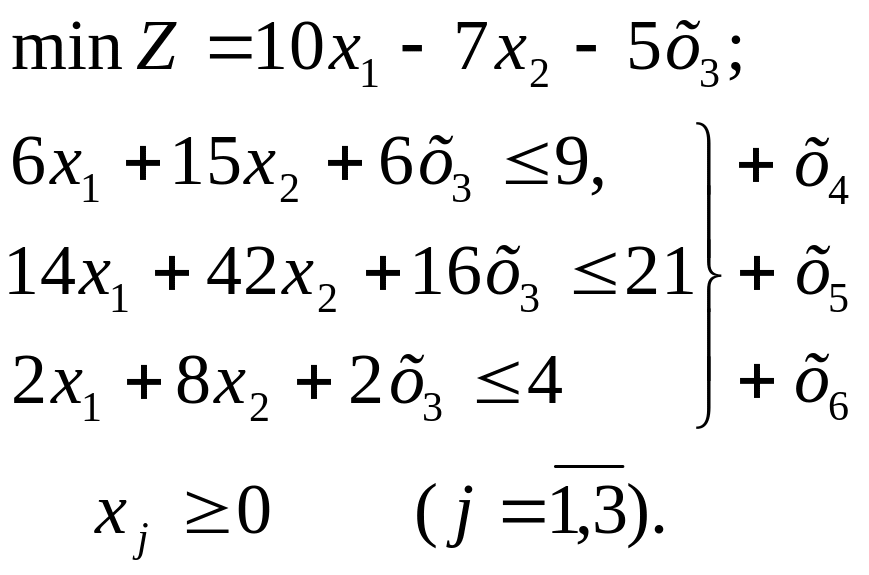
Решение Приведем задачу к каноническому виду:

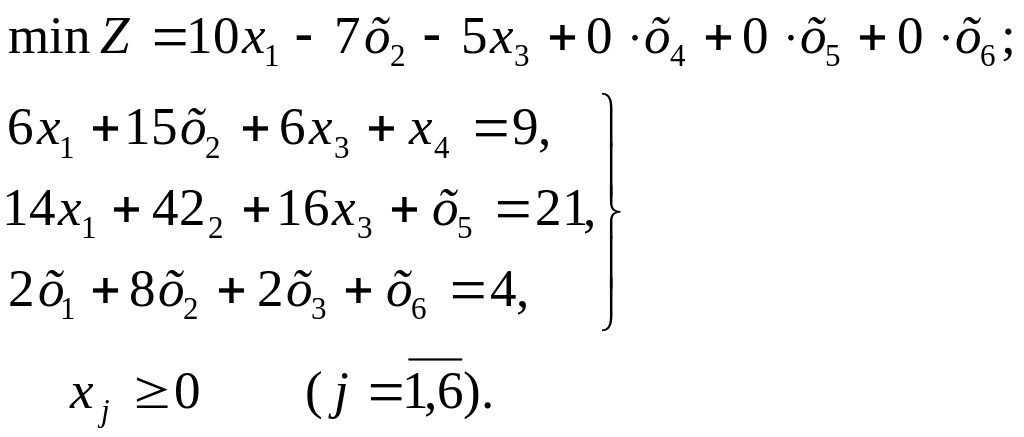
Система ограничений имеет предпочтительный вид. Начальный опорный план

2-й случай. Пусть система ограничений имеет вид

Перейдем к каноническому виду путем введения дополнительных переменных х_n+i  0 (i=1…m):

Теперь система ограничений, вообще говоря, не имеет предпочтительного вида. В этом случае вводят искусственный базис путем перехода к М- задаче:

где в целевой функции знак «-» относится к задаче максимизации. Если некоторые из уравнений исходной системы ограничений имеют предпочтительный вид, то в них не вводят искусственные переменные. Начальный опорный план М – задачи имеет вид

Между оптимальными планами исходной задачи и М – задачи имеется следующая связь: если в оптимальной задачи и М – задачи все искусственные переменные w_i^* равны нулю, то значения оставшихся координат плана х^* дадут оптимальный план исходной задачи.

Пример. Найти начальный опорный план задачи

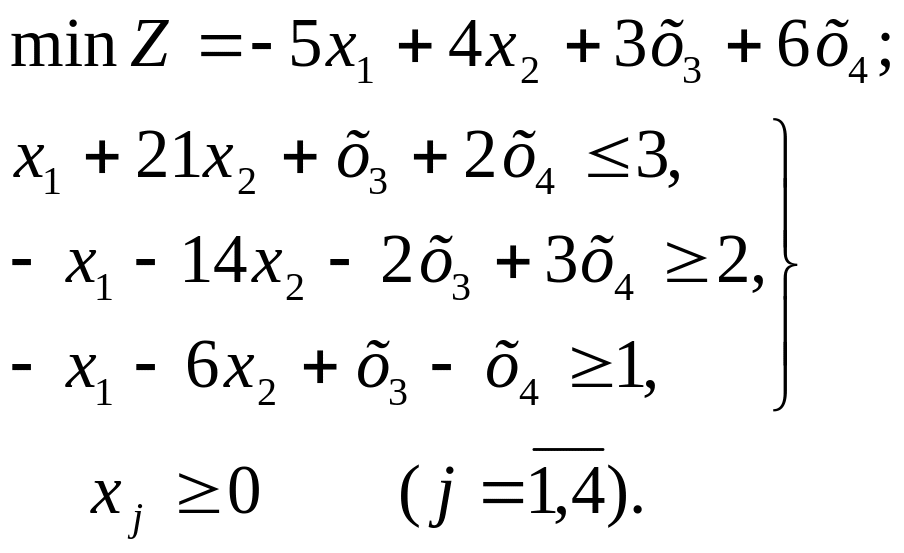
Решение. Вводя дополнительные х₅, х₆, х₇ и искусственные переменные, переходим к задаче в каноническом виде и к М – задаче:

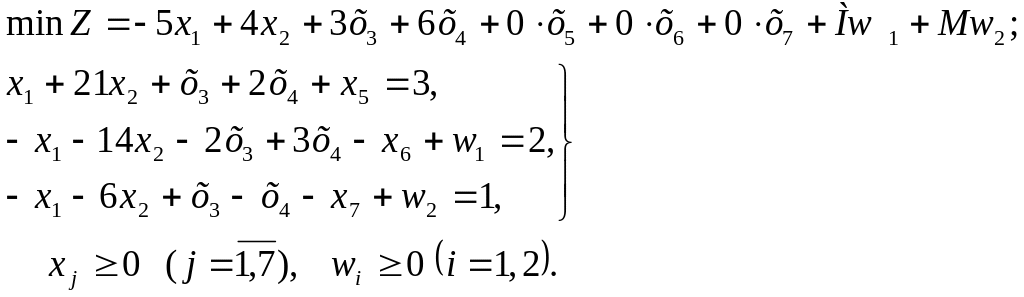
Ее начальный опорный план