87. Свойства сходящихся рядов.

1. Если ряд (l) сходится, то сходится и любой ряд, полученный из него отбрасыванием конечного числа членов. Ряд

полученный отбрасыванием первых

п членов суммы (l), называется п-м остатком ряда. Таким образом, ряд (l) и любой его остаток сходятся или расходятся одновременно.

2. Если каждый член сходящегося ряда (l), сумма которого равна S, умножить на некоторое число k, то полученный ряд также сходится, и его сумма равна kS.

3. Если даны два сходящихся ряда и

с суммами S и Т соответственно, то новый ряд полученный почленным сложением исходных рядов, также сходится, и его сумма равна S + T.

4. Если ряд (1) сходится, то сходится и любой ряд, полученный из него группировкой слагаемых, и суммы рядов одинаковы.

88. Необходимое условие сходимости числового ряда.

Теорема 5.1 (необходимый признак сходимости). Если ряд сходится, то предел его общего члена равен нулю.

Эквивалентная формулировка: Если предел общего члена ряда не равен нулю.или не сугцествует, то данный ряд расходится.

Доказательство. Пусть данный ряд сходится и его сумма равна S. Для любого натурального п имеем S_n= S_n-₁ + а_п или

A_n=S_n-S_n-1

При п -> infinity обе частичные суммы S_n и S_n-1 стремятся к пределу S, поэтому из равенства следует, что

Подчеркнем еще раз, что мы установили только необходимое условие сходимости ряда, т.е. усдовие, при нарушении которого ряд не может сходиться. С помощью этого признака можно дока­зывать только расходимость ряда

89. Числовые ряды с неотрицательными членами.

Числовой ряд называется рядом с положительными членами, если общий член ряда а_п >0 для любого n=1,2,.... Критерием сходимости для таких рядов служит ограниченность последовательности частичных сумм ряда.

При решении задач на сходимость рядов первым шагом является проверка выполнения необходимого условия сходимости, т.е.

90. Критерий сходимости числовых рядов с неотрицательными членами.

Теорема 5,2. Для того чтобы ряд с положительными члена­ми сходился, необходимо и достаточно, чтобы последователь­ность его частичных сумм была ограничена.

91. Признаки сравнения, признак Даламбера и Коши, интегральный признак для числовых рядов с неотрицательными членами.

Признак Даламбера (в предельной форме). Пусть для числового ряда с положительными членами существует конечный предел . Тогда при d<1 ряд сходится, а при d>1 ряд расходится.

Первый признак сравнения. Пусть члены двух числовых рядов с положительными членами и 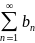удовлетворяют условию a_n<=b_n (n=1,2,…). Тогда из сходимости «большего» ряда следует сходимость «меньшего» ряда , а из расходимости «меньшего» ряда следует расходимость «большего» ряда.

Второй признак сравнения. Пусть для двух числовых рядов с положительными членами и существует конечный предел . Тогда оба ряда сходятся или расходятся одновременно.

Интегральный признак сходимости. Пусть члены числового ряда a_n=f(n) являются значениями неотрицательной непрерывной функции f(x), монотонно убывающей на луче [1; + oo). Тогда ряд и несобственный интеграл сходятся или расходятся одновременно.

Признак Коши. Пусть для числового ряда с положительными членами существует конечный предел . Если к < 1, то ряд сходится, а при к > 1 ряд расходится.