Мат_модели

Федеральное государственное образовательное учреждение высшего

профессионального образования

ФИНАНСОВАЯ АКАДЕМИЯ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ

Кафедра «Математика и финансовые приложения»

В.М. Гончаренко

Математические методы и модели исследования операций

Руководство к решению задач

Для студентов института

«Математические методы в экономике»

Москва 2006

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

§1. Каноническая и стандартная форма

задачи линейного программирования

Задачей линейного программирования называется задача оптимизации вида

f = c1x1 + c2 x2 +K+ cn xn + c0 → max (min)

тема ограничений задает в пространстве Rn выпуклое допустимое множество X , а любая точка x = (x1, x2 ,K, xn ) X называется допустимым решением задачи линейного программирования. Допустимое решение, на котором целевая функция достигает оптимального значения, называется оптимальным решением задачи линейного программирования.

Если система ограничений состоит только из уравнений и тривиальных неравенств, то говорят, что задача имеет каноническую форму, если же в системе ограничений имеются только неравенства, то говорят о стандартной форме задачи линейного программирования. В зависимости от метода решения, задачу необходимо привести к канонической или стандартной форме.

3

Пример 1. Привести к канонической форме задачу линейного программирования

z = 4x1 +2x2 −13x3 +2x4 − x5 → max

x1 −7x2 + x3 − x4 ≤ 9,5x1 +8x2 − x3 + x5 =10,

12x1 +8x2 +2x3 −3x4 + x5 ≥11,xi ≥ 0,i =1,K,5.

Решение. Согласно входящим в ограничения неравенствам, можно ввести балансовые переменные x6 ≥ 0, x7 ≥ 0 , такие, что эти условия при-

водятся к виду

x1 −7x2 + x3 − x4 + x6 = 9,

12x1 +8x2 +2x3 −3x4 + x5 − x7 =11,

и исходная задача переписывается в канонической форме

z = 4x1 +2x2 −13x3 +2x4 − x5 → max

x1 −7x2 + x3 − x4 + x6 = 9,5x1 +8x2 − x3 + x5 =10,

12x1 +8x2 +2x3 −3x4 + x5 − x7 =11,

xi ≥ 0,i =1,K,7.

Пример 2. Привести к стандартной форме задачу линейного программирования

z = 2x1 + x2 +3x3 + x4 → max

x1 +2x2 +5x3 − x4 = 4,x1 − x2 − x3 +2x4 =1,

xi ≥ 0,i =1,K,4.

Решение. Рассмотрим систему нетривиальных ограничений

x1 +2x2 +5x3 − x4 = 4,x1 − x2 − x3 +2x4 =1,

и выделим (методом Гаусса) базисные и свободные переменные:

Итак, получаем систему

4

x1 + x3 + x4 = 2,x2 +2x3 − x4 =1,

из которой выражаем базисные неизвестные

2 − x3 − x4 = x1 ≥ 0,1−2x3 + x4 = x2 ≥ 0,

и исключаем их из целевой функции

z = 2x1 + x2 +3x3 + x4 = 2(2 − x3 − x4 ) +(1−2x3 + x4 ) +3x3 + x4 = −x3 +5 .

Получим задачу в стандартной форме, равносильную исходной:

z = −x3 +5 → max

x3 + x4 ≤ 2,2x3 − x4 ≤1,x3 ≥ 0, x4 ≥ 0.

Задачи для самостоятельного решения

Найти каноническую форму следующих задач линейного программирования

Привести задачи линейного программирования к стандартному виду:

5

§2. Графический метод решения задач линейного программирования

Если задача линейного программирования задана в стандартной форме в R2 , то для ее решения используют графический метод, который состоит в следующем.

1.Строится допустимое множество X , заданное системой ограничений, как пересечение полуплоскостей, определяемых каждым из входящих в эту систему неравенств. Если X – пустое множество, то задача решений не имеет.

2.Если X – непустое множество, то рассматриваются линии уровня целевой функции f = c1x1 + c2 x2 + c0 . Они определяются как прямые

вида c1x1 +c2 x2 = const с общим вектором нормали n = (c1,c2 ), определяю-

щим направление роста функции f . Смещая линии уровня в направле-

нии вектора n , находим первую точку x* = (x1*, x2* ) пересечения такой ли-

нии с множеством X . Тогда fmin = f (x* ) является минимальным значени-

ем функции f на X . Аналогично, если x* = (x1*, x2* ) – последняя точка пе-

ресечения линии уровня с множеством X , то fmax = f (x* ) – максимальное значение функции f на X . Если при перемещении линии уровня в на-

правлении n последняя имеет пересечения с X при сколь угодно большом значении константы, то fmax = +∞. Если же, наоборот, линии уровня имеют пересечения с X при сколь угодно большом по модулю отрицательном значении постоянной, то fmin = −∞.

Пример 3. Решить графически следующую задачу линейного программирования

6

z =3x1 + x2 −10 → max

7x1 + x2 ≥ 29,3x1 + 2x2 ≤ 25,

4x1 − x2 ≤15,xr ≥ 0.

Решение. Построим допустимую область X , т.е. множество на плоскости, определяемое системой

7x1 + x2 ≥ 29,3x1 +2x2 ≤ 25,

4x1 − x2 ≤15,xr ≥ 0.

Для этого построим сначала прямые l1 : 7x1 + x2 = 29 , l2 : 3x1 +2x2 = 25 и l3 : 4x1 − x2 =15 на плоскости (x1, x2 ), а затем найдем их точки пересечения.

Точку пересечения прямых l1, l2 находим как решение системы уравне-

ний

7

Каждая из прямых разбивает плоскость на две полуплоскости, а каждое неравенство, входящее в систему ограничений, задает одну из полуплоскостей. Для того чтобы установить, какая из полуплоскостей определяется неравенством, необходимо взять произвольную («пробную») точку, не лежащую на прямой и проверить, удовлетворяет ли она соответствующему неравенству. Если неравенство выполнено, то неравенство определяет полуплоскость, содержащую «пробную» точку, а если неравенство не выполняется, то его решением является другая полуплоскость. Решением системы неравенств будет пересечение соответствующих плоскостей. В нашем случае это треугольник ABC . Построив вектор нормали n = (3;1) , убеждаемся, что решением задачи на максимум является точка B(5;5) и z(B) = 3 5 +5 −10 =10 .

Ответ. zmax = z(B) =10 .

Пример 4. Решить графически следующую задачу линейного программирования

z = 2x1 + x2 +3x3 + x4 → max

x1 +2x2 +5x3 − x4 = 4,x1 − x2 − x3 +2x4 =1,

xi ≥ 0,i =1,K,4.

Решение. Формально задача является, вообще говоря, задачей линейного программирования в пространстве R5 . Но ее можно свести к задаче на плоскости R2 , приведя к стандартной форме, как это было сделано в примере 2 § 1. Таким образом, имеем задачу

z = −x3 +5 → max

x3 + x4 ≤ 2,2x3 − x4 ≤1,x3 ≥ 0, x4 ≥ 0.

Строим на плоскости прямые l1 : x3 + x4 = 2, l2 : 2x3 − x4 =1 , находим их точку пересечения и в качестве допустимого множества получаем

8

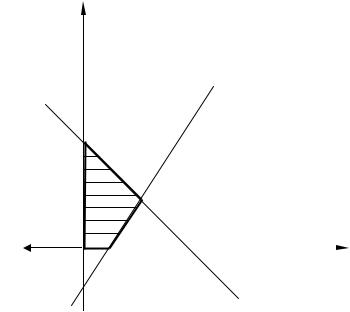
x4

A

B

O

ным множеством, на котором достигается максимальное значение функ-

графическим методом.

Решение. Выразим базисные неизвестные x3 , x4 из ограничений

x3 = 3 − x1 + x2 ≥ 0,x4 = 2 + 2x1 − x2 ≥ 0,

и получаем задачу в стандартной форме

9