1.Определение числовой функции. Способы задания функций.

Пусть имеются два множества Х и Y. Пусть указано правило, по которому каждому элементу х принадлеж. Х сопоставляется некоторый(единств.) элемент у принадлеж. У. Тогда говорят, что задана функция из Х в У. Числовая функция характерез. тем, что оба множества Х и У состоят из чисел х- аргумент, у- функция. 3 способа задания: 1)Табличный (область определения из конечного множества чисел) 2) Аналитический –задание с помощью формулы. 3) Графический.4) словесный.

2. Понятие обратной функции.

Если существует отображение У в Х, такое, что каждому соотв. единственное значение х, то существует обратная функция х=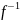 (y)

3. Понятие сложной функции. Пусть даны две функции z = f(y) и у = g(x). Сложной функцией (или композицией функций f и g) называется функция z = h(x), значения которой вычисляются по правилу h(x) = f(g(x)) (т. е. сначала вычисляется g(x), при этом получается некоторое число у, а затем вычисляется значение в точке у).

4. Определение предела последовательности.

число А называется пределом последовательности {Хn}, если для любого положительного Е существует номер n0, начиная с которого все члены последовательности отличаются от А по модулю меньше, чем на Е.

5. Правила вычисления пределов сходящихся последовательностей.

1) lim(Xn + Yn)= a+b 2) lim (Xn*Yn)=a*b 3)lim 1/Yn = 1/b, если у и б не равны 0 4) lim Xn/Yn= a/b

6. Определение ограниченной последовательности.

Ограниченная последовательность (ограниченная с обеих сторон последовательность) — это последовательность, ограниченная и сверху, и снизу. Ограниченная сверху последовательность — это последовательность элементов множества X, все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется верхней гранью данной последовательности. Ограниченная снизу последовательность — это последовательность элементов множества X, для которой в этом множестве найдётся элемент, не превышающий всех её членов. Этот элемент называется нижней гранью данной последовательности.

7. Определение бесконечно малой последовательности.

Бесконечно малая последовательность — это последовательность, предел которой равен нулю.

8. определение беск. большой последовательности.

Послед-ь {Xn} называется бб, если для любого положительного числа ε существует номер N такой, что при n > N выполняется неравенство |Xn| > ε. (lim (n→∞) Xn = ∞ ).

9.Определение монотонных последовательностей.

Последовательнсть {Хn} назыв.: возрастающей, если Хn<X(n+1) для всех n; невозрастающей, если Хn≤X(n+1) для всех n; убывающей, Хn>X(n+1) для всех n; неубывающей, Хn≥X(n+1) для всех n

10. определение предела функции в точке.

Число а называется пределом функции f (x) в точке X₀ (или пределом при X→ X₀) если для любой сходящейся к точке X₀ послед-и значений аргумента, отличных от X0, соответствующая послед-ь значений функции сходится к числу а, т. е.

lim Xn = X₀ (Xn ≠ X₀) => lim f(Xn) = a; lim (X→ X₀) f(x) = a.

11.определение бесконечно малой функции.

Функция 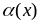называется бесконечно малой пр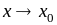и , если

.

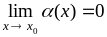12.определение бесконечно большой функции.

Функцию 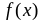называют бесконечно большой при Х , стремящемся к Х₀, если для любой последовательности

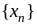
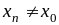( ) значений аргумента, стремящейся к Х₀, соответствующая последовательность значений функции является бесконечно большой. Записывают: .

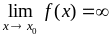13. Первый замечательный предел.

lim (sinx/x)=1 при x→0

14. Второй замечательный предел

Lim(1+ 1/n)ⁿ = e

x→∞

15. Дайте определения односторонних пределов функции в точке

Число А называется правым пределом функции f(x) при х → а, если для любого ξ > 0 существует такое δ, что для всех х, удовлетворяющих неравенству а < х < а + δ, выполняется неравенство | f(x) - А |< ξ.

Число А называется левым пределом функции f(x) при х → а, если для любого ξ > 0 существует такое δ, что для всех х, удовлетворяющих неравенству а - δ < х < а, выполняется неравенство | f(x) - А |< ξ.

16. Функция, непрерывная в точке. Функция y = f (x), определенная в некоторой окрестности точки х₀ , называется непрерывной в этой точке, если предел функции в точке х₀ существует и равен значению в этой точке: lim _{х → х0} f(x) = f(x₀).

Функция y = f (x) называется непрерывной в точке х = х₀ , если эта функция определена в какой-либо окрестности точки х₀ и в самой точке х₀ , и если бесконечно малому изменению аргумента соответствует бесконечно малое изменение функции.

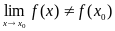17.Точка разрыва. Точка х₀ называется точкой разрыва функции f(x), если или 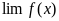не существует.

Разрыв 1 рода (скачок) если в этой точке функция имеет конечные, но не равные друг другу левый и правый пределы.

Разрыв 2 рода (бесконечный), если в этой точке функция f(x) не имеет по крайней мере одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.

Разрыв 3 рода (устранимый), если функция не существует в точке х₀ или если значение функции в точке х₀ не совпадает со значением односторонних пределов.

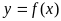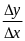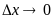18.определение производной в точке Пусть функция определена в некоторой окрестности точки x₀(∆x=x-x₀). Производной функции в точке x₀ называется lim , когда (при условии, что lim существует). Обозначение .

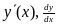19.Определение дифференцируемой функции в точке х. Если функция y = f(x) имеет производную в точке х₀ , то мы говорим, что функция дифференцируема в этой точке.

20. Дифференциалом функции в точке х₀ называется линейная относительно приращения аргумента часть приращения функции в этой точке, эквивалентная всему приращению.

df(х₀)= f ′ (х₀) ∆х; ∆х=dх; df(х₀)= f ′ (х₀) dх