Математика облигаций

Москва 2012

2

1. Облигации и их оценивание

1.1. Общие характеристики облигаций

Ценная бумага с фиксированным доходом - это бумага, по которой эмитент

(заемщик) соглашается произвести ряд платежей, сроки и размеры которых оговариваются в контракте.

Ценные бумаги с фиксированным доходом можно разделить на две категории:

-долговые обязательства (облигации),

-привилегированные акции.

По долговому обязательству заемщик осуществляет процентные выплаты. Мы будем называть ценные бумаги, представляющие собой долговые обязательства,

облигациями.

Облигация - ценная бумага, удостоверяющая право ее держателя на получение номинальной стоимости облигации или иного имущественного эквивалента от лица, выпустившего облигацию, в предусмотренный ею срок.

Другими словами, облигация - это долговая ценная бумага, дающая право ее держателю на получение фиксированного дохода, в виде регулярных процентных платежей.

Простой облигацией (или просто облигацией) будем называть любую долговую ценную бумагу, не дающую ее держателю никаких имущественных и личных неимущественных прав, кроме получения фиксированного дохода.

Параметры облигации.

Облигация характеризуется рядом количественных параметров. Эти параметры делятся на два класса: неизменяемые (реквизиты) и изменяемые (текущие) параметры.

К неизменяемым параметрам относятся:

-F - номинальная стоимость или номинал облигации,

-c - купонная (годовая) ставка,

-v - частота купонных выплат (раз/год),

-h=1/v – купонный период (в годах)

-t0 - момент ( д0 - дата) эмиссии,

-t1 - момент ( д1- дата) первой купонной выплаты,

-tпог - момент ( дm - дата) погашения,

-m0 = tпог - t0 - срок обращения (в годах).

Кроме неизменных параметров (реквизитов) облигация обладает рядом

изменяющихся со временем параметров. Так для момента времени t , t0 ≤ t ≤ tпог определены следующие параметры:

-m = mt = tm - t - оставшийся срок до погашения (в годах),

-M=Mt = v m – оставшийся срок до погашения, измеренный в купонных периодах,

-P = Pt = P (t) – текущая рыночная цена облигации,

-y = yt – (текущая) доходность к погашению,

-и другие.

Об этих и других параметрах будет подробно рассказано ниже.

В дальнейшем мы часто будем в обозначении облигации указывать набор значений ее важнейших параметров – своего рода паспорт облигации и писать

B = B(F, c, m0, v).

Например, B(1000, 10%, 20, 2) означает облигацию с номиналом 1000, купонной ставкой 10%, сроком обращения 20 лет, причем купоны выплачиваются дважды в году.

Когда момент времени подразумевается, говорят о текущем моменте и соответствующих текущих характеристиках: текущей цене или просто цене, текущем сроке до погашения ит.п. Индекс времени в обозначениях текущих характеристик тогда обычно опускается. Пишут просто цена P, срок погашения m

3

ит.д. Однако при исследовании зависимости от переменного параметра он обязательно указывается в выражении изучаемой величины: например P(i) при исследовании зависмости цены от рыночной ставки.

Купонные выплаты по облигации - это периодические процентные выплаты, производимые держателю облигации в течение срока жизни облигации.

Промежуток между двумя последовательными купонными выплатами называется купонным периодом. Его длину в годах будем обозначать h. Если купонные выплаты производятся ежемесячно, то h = 1/12, если ежеквартально, то h = 1/4, если раз в полугодие - h = 1/2, если раз в год, то h = 1.

Часто вместо купонного периода h задают кратность купонных выплат в году v или кратность начисления купонного дохода за год. Ясно что между этими

По отношению к облигации под купоном часто понимается годовая купонная ставка, т.е. процентная ставка, которая после умножения на номинальную стоимость даёт денежную величину годовой купонной выплаты. В дальнейшем годовую купонную ставку будем обозначать c. С ней связана ставка за купонный

дальнейшем суммарные купонные выплаты за один год будем обозначать С. Очевидно, что С = c F.

Купонные выплаты за период и суммарные купонные выплаты за год связаны

характеризуется набором параметров: номиналом - F , сроком до погашения - m, годовой купонной ставкой - c, купонным периодом – h или частотой купонных выплат - v.

Существуют облигации, по которым в течение всего срока до погашения не производится никаких выплат. Вместо этого и номинал, и проценты выплачиваются в день погашения. Такие облигации называются бескупонными (чисто дисконтными) облигациями или облигациями с нулевым купоном (zero-coupon bonds).

Инвестор при вложении в бескупонные облигации получает проценты в виде разности между номиналом и ценой покупки.

Пример 1.1. Купонная ставка облигации равна 10%, а номинал облигации равен 1000 руб. Найти размер купонных выплат по этой облигации. Купонный период – год.

Решение. Мы имеем c = 10% = 0,1. Номинал облигации F = 1000 руб. Значит купонные выплаты по такой облигации C = c F = 1000 0,1 руб. = 100 руб. █

Курс облигации. Покупатель, приобретая облигацию, предоставляет эмитенту ссуду, т.е. он является кредитором. Рыночная цена облигации P может отличаться от ее номинальной стоимости F. Величина

K FP 100%

называется курсом облигации.

Курс облигации – цена выраженная в процентах от ее номинала может меняться со временем. Обычно значения курса (или котировка) указывается без знака процентов.

4

Пример 1.2. Определить рыночную цену облигации, если курс облигации 95, а номинальная стоимость (номинал) 1000 руб.

Решение. Мы имеем F = 1000 руб., K = 95 следовательно P = K·F/100=950(руб.) █

1.2. Оценивание облигаций

Цена любого финансового инструмента равна текущей стоимости ожидаемого денежного потока от этого финансового инструмента. Таким образом, для определения цены необходимо:

-оценить ожидаемый денежный поток,

-оценить соответствующую ставку дисконтирования (требуемую доходность). Первым шагом в вычислении цены облигации является определение ее

денежного потока. Поток платежей (денежный поток) для купонной облигации состоит из:

-периодических купонных выплат до даты погашения,

-выплаты номинала в дату погашения.

Для указания моментов времени, в которые осуществляются платежи по облигации, необходимо использование временной шкалы (системы временных координат). Существуют три основные шкалы: годовая шкала T, шкала купонных периодов Th, и календарная шкала K. В годовой шкале единицей времени служит год, в шкале купонных периодов очевидно купонный период и в календарной шкале единичным элементом является дата д=(d,m,y) и сроки обычно задаются в днях, месяцах, годах и т.д. Все формулы мы будем записывать только в модельных шкалах T и Th а практическое их использование будет осуществляться с помощью, так называемых временных правил, позволяющих по данным календарной шкалы находить соответствующие параметры в шкалах T и Th.

Поток платежей облигации.

Пусть с - купонная ставка облигации, F- номинальная стоимость облигации, размер купонной выплаты Сh, h - купонный период, а M – общее число купонных периодов до погашения. Выберем в качестве начального момента t0=0 момент эмиссии.

Тогда поток платежей в годовой шкале T имеет вид, изображенный на рис. 1.1.

Рис. 1.1. Поток платежей по купонной облигации

Работа с дробными (в годовой шкале) периодами при h≠1 часто не очень удобна, поэтому в дальнейшем, если не оговорено противное, мы будем пользоваться шкалой купонных периодов Th. В шкале купонных периодов базовым (единичным) элементом шкалы является купонный период. Поток платежей по облигации в этой шкале изображен на следующей диаграмме:

Рис. 1.2. Стандартный поток платежей по купонной облигации

Стечением времени срок до погашения облигации сокращается и в этом случае

вмомент k-ой купонной выплаты останется лишь M=M0–k купонных периодов и

5

выплат. Ниже мы не будем специально оговаривать, является ли M исходным (т.е M0) или оставшимся числом купонных периодов, а будем просто говорить об облигации со сроком до погашения M (в шкале Th) или m (в шкале T)

Пример 1.3. Найти поток платежей облигации, если купонная ставка облигации равна 10%, а номинал облигации равен 1000 руб. Купонный период – полгода. Срок облигации 1,5 года.

Решение. Мы имеем c = 10% = 0,1, купонный период h = 1/2, количество купонных периодов до погашения M = 3. Номинал облигации F = 1000 руб. Значит

█

Ставка дисконтирования.

Выбор ставки дисконтирования определяется целями оценивания. Во-первых, это может быть требуемая ставка доходности, т.е. доходность, которую желает получить инвестор покупающий облигацию. В этом случае, цена, полученная в результате оценивания, сравнивается с фактической рыночной ценой облигации, и на основании этого сравнения делается решение о покупке (или продаже) облигации. Во-вторых, это может быть альтернативная доходность, т.е. доходность по аналогичным с оцениваемой облигацией активам. В этом случае оцениваемая облигация сравнивается по инвестиционной привлекательности с другими активами, обращающимися на рынке. Ниже, ставка дисконтирования считается заданной и в рамках модели оценивания принятой в этой главе, она считается равновесной рыночной ставкой, по которой оцениваются все платежи, к какому бы моменту времени они не относились. Такая модель соответствует плоской временной структуре процентных ставок (flat time structure of interest rate).

Внутренняя цена (стоимость) облигации. Внутренняя цена (стоимость)

облигации – это текущая стоимость денежного потока, задающего облигацию. Она определяется путем сложения следующих двух значений:

1)текущей стоимости купонных выплат,

2)текущей стоимости номинала (или суммы погашения).

Другими словами стоимость облигации может быть получена путем дисконтирования будущих платежей по облигации, относительно выбранной процентной ставки.

В этом параграфе мы будем оценивать облигацию только с целым числом купонных периодов до погашения, или, иными словами, оценка производится на момент купонной выплаты без учета текущего купона.

Напомним, что для любого потока платежей

СF = {(t1,C1); (t2,C2);…, (tn,Cn)}

заданного в шкале Th, и ставки ih за период h, текущая стоимость потока относительно момента t0 определяется формулой:

6

Для облигаций в шкале купонных периодов это приводит к следующей формуле (полагая t0=0 и в качестве потока СF текущий поток СFB платежей)

где ih - процентная ставка (ставка дисконтирования) за купонный период h, а М – число купонных платежей. Для облигации со сроком обращения M0 в качестве момента оценивания можно брать любой момент купонного платежа tk и тогда говорят об оценивании на момент k-ой купонной выплаты. В этом случае, цена часто обозначается Pk. Оставшийся срок до погашения будет М=M0-k.

Используя формулу для суммы геометрической прогрессии можно получить сокращенную формулу для стоимости облигации:

Рассмотрим три особых случая оценивания облигации.

Заметим, что сокращенная формула (1.2 ) определена только при ненулевых значениях ставки ih. Однако основная формула (1.2) годится и в этом случае. Получаемое при этом значение

будет, как показано ниже максимальным возможным значением цены облигации.

Следующий случай касается бескупонных облигаций. Для бескупонной облигации Zm со сроком погашения m лет формула стоимости облигации приобретает особенно простой вид:

где iэф – эффективная годовая ставка.

Рыночная процентная ставка обычно задается как нормированная (приведенная к году) ставка. Это либо номинальная годовая ставка i(v) с периодом начисления равным купонному периоду h, и в этом случае ставка за купонный период ih = i(v)/v, либо это эффективная годовая ставка iэф, и тогда ih = (1+ iэф)h-1.

На практике, в анализе купонных облигаций, чаще используется (более удобная) номинальная годовая ставка, которую мы будем обозначать просто i,

подразумевая, что период начисления всегда равен купонному периоду.

Наконец, последний особый случай касается так называемых бессрочных облигаций (консолей) не имеющих срока погашения. Поток платежей такой облигации представляет собой бессрочную ренту купонных платежей. Формально оценка такой облигации получается предельным переходом в формуле (1.2 ) при неограниченном увеличении срока до погашения M:

Пример 1.4. Определить внутреннюю цену облигации, заданной параметрами: m = 2 года, c = 7% годовых , F = 1000 руб., относительно ставки i = 10% годовых, для купонных платежей а) v =1 раз; б) v =2 раза в год.

7

Решение. а) Размер купонной выплаты C = 0,07 1000/2 = 70 (руб.). Купонные выплаты годовые и M = m = 2, и ставка за купонный период равна i1 = i=10%.

Подставляем данные в формулу (1.2):

б) Размер купонной выплаты С1/2 = с F/v = 35 (руб.). Купонные выплаты годовые и M = 4, и ставка за купонный период равна i1/2 = i/2=5%.

Подставляем данные в формулу (1.2):

Пример 1.5. Определить внутреннюю цену облигации, заданной параметрами: m = 10 лет, c = 14%, F = 100 руб., v = 2, относительно номинальной ставки i(2) = 10%

с полугодовым начислением, используя формулу (1.2')

Решение. Размер купонной выплаты Ch = c F/v = 7 руб. Купонные выплаты полугодовые и M = 2m = 20. Наконец ih= i (2)/2 = 5% (за купонный период).

Подставляем данные в формулу (1.2'):

Облигации, котирующиеся по номиналу, с премией и с дисконтом.

Рассмотрим, теперь, три случая взаимоотношения рыночной и купонной ставок:

1) ch= ih

Если цена облигации совпадает с номиналом, то говорят, что облигация котируется по номиналу. Такие облигации в англоязычной литературе называют также текущими (current bond).

Если цена облигации больше номинала, то говорят, что облигация котируется

спремией. Такие облигации называются премиальными.

3)ch < ih. Тогда

8

Если цена облигации меньше номинала, то говорят, что облигация котируется

сдисконтом. Такие облигации называются дисконтными.

Впоследних двух случаях можно дать простое словесное доказательство этим свойствам. Поскольку при c = i мы показали, что P=F, и, кроме того, очевидно (см. ф-лу 1.2), что с ростом купонной ставки (при неизменности других параметров) цена облигации растет, то ясно, что при c>i цена будет больше P>F, а при c<i меньше

P<F номинала.

Свойства цен облигаций.

Формулы (1.2) и (1.2') задают стоимость Р=P(B) облигации B как функцию ее параметров

Pt(B) = PVt(F, c, v ; m, i).

Для практических целей важно знать характер зависимости стоимости облигации от этих параметров. Ниже мы приведем ряд утверждений о свойствах этой зависимости. Подчеркнем, что пока речь идет о стоимости облигации на моменты купонных выплат (т.е. на дискретный набор моментов времени).

.

Свойство 1. Стоимость облигации монотонно убывает при росте процентной ставки.

Это утверждение достаточно очевидно, поскольку согласно формуле (1.2) стоимость есть конечная сумма слагаемых вида 1/(1+ ih)k, каждое из которых убывает с ростом ставки.

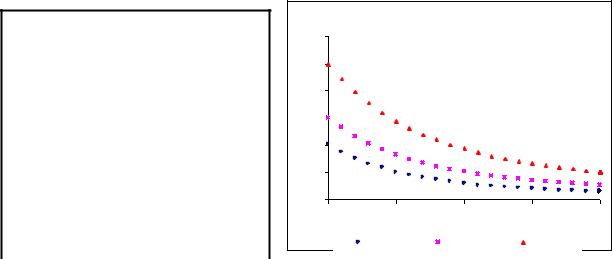
Пример 1.6. В таблице 1.1 приведены значения цены облигации с номиналом F =100, сроком погашения 20 лет и годовыми купонами для трех значений купонной ставки: с=5%, с=10%, с=20%. На рис. 1.3 приведен график зависимости стоимости этих облигаций от рыночной ставки.

Из графика видно, что максимальное значение Pmax цены достигается в точке i = 0 и равно, как следует из формулы (15.2') сумме купонных выплат и номинала

Pmax = mC + F= MCh+F. █

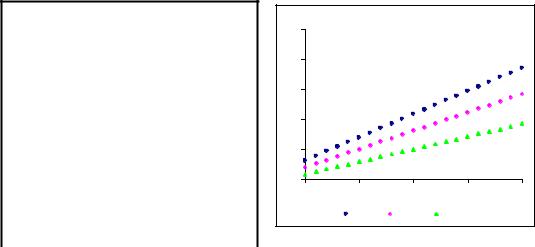
Свойство 2. Стоимость облигации линейно зависит от номинала и купонной ставки.

Для доказательства данного свойства рассмотрим формулы (1.2-1.3 стоимости облигаций:

Пример 1.7. В таблице 1.2 приведены значения цены облигации с номиналом F =100руб., сроком погашения 10 лет и годовыми купонами для трех значений рыночной процентной ставки: i=5%, i=10%, i=20%. На рис. 1.4 приведен график зависимости стоимости этих облигаций от купонной ставки. █

Свойство 3. Стоимость облигации - возрастающая функция срока до погашения, если ставка купона больше рыночной процентной ставки, убывающая функция, если ставка купона меньше рыночной процентной ставки, и ее стоимость не зависит от срока до погашения при равенстве этих ставок (за купонный период!).

Пусть F, ch, ih- заданные, фиксированные величины. Не теряя общности, положим v =1. Тогда стоимость облигации есть функция P = P(m) одной переменной m – срока погашения. Для целых значений m она определяется равенством:

P(m) = F [c/i + (1- c/i)/(1+ i)m] (1.3)

Поведение функции P(m) с ростом m зависит от знака (1- c/i). Поскольку 1/(1+i)m убывает с ростом m, то для 1- c/i < 0, т.е. при c>i функция P(m) возрастает от значения F при m = 0 до C/i при m . Для 1-c/i>0, т.е. c<i функция P(m) монотонно убывает от F при m = 0 до C/i при m . Наконец, для 1-c/i = 0, т.е. при c = i функция P(m) = C/i - постоянна (не зависит от m) равна C/i= C/с=F

номиналу.

Пример 1.8. Рассмотрим три облигации с одинаковым номиналом F =100руб. и купонными ставками c1 = 5% и c2 = 10% и c3 = 20% соответственно. Пусть номинальная рыночная ставка равна i=10% годовых. Построить таблицу и график зависимости стоимости от срока погашения для этих облигаций при рыночной ставке 10% годовых

10