
- •Определение первообразной для ф-ции на промежутке .
- •Свойства неопределенного интеграла
- •Свойства определенного интеграла
- •На ограниченном промежутке
- •Функция нескольких переменных
- •Поверхности (линии) уровня функции нескольких переменных.
- •Свойства функций, непрерывных на замкнутом ограниченном множестве: ограниченность, достижение наибольшего и наименьшего значений.
- •Частные производные функции нескольких переменных.
- •Производная сложной функции.
- •Формула Тейлора для функции нескольких переменных с остаточным членом в форме Лагранжа.
- •Кратные интегралы и их свойства. Условия интегрируемости функции.
- •Ряды Тейлора (Маклорена).
- •Достаточное условие разложимости функции в ряд Маклорена.
- •109. Общее решение однородной системы линейных дифференциальных уравнений в случае существования базиса из собственных векторов.
Функция — это закон или правило, согласно которому каждому элементу x из множества X ставится в соответствие единственный элемент y из множества Y. Задается графически или аналитически.
Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией.Функция g : Y->X является обратной к функции , f : X -> Y если выполнены следующие тождества: f(g(y))= y для всех y принадлежащих Y g(f(x)) = x для всех х принадлежащих Х
Сложная функция – функция от функции. Если величина y является функцией от u, то есть у = f (u), а и, в свою очередь, функцией от х, то естьu = h(х), то у - cложная функция от х, то есть y = f (h(x)), определённой для тех значений х, для которых значения h(х) входят в множество определения функции f (u).
Последовательность {xn} называется сходящейся, если существует такое число а, что последовательность{xn-a} является бесконечно малой. При этом число а называется пределом последовательности {xn}
5) Правила вычисления пределов сходящихся последовательностей
Пусть
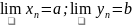 тогда:
тогда:
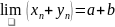 (предел
суммы равен сумме пределов)
(предел
суммы равен сумме пределов)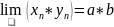 (предел
произведения равен произведению
пределов)
(предел
произведения равен произведению
пределов)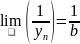 (если
все yn, а также b отличны от нуля)
(если
все yn, а также b отличны от нуля)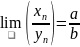 (если
все yn, а также b равны 0)
(если
все yn, а также b равны 0)Ограниченная последовательность. Последовательность (чисел, точек и т.п.), члены которой образуют ограниченное множество, называется ограниченной. Аналогично последовательность называется ограниченной сверху (снизу), если ее члены образуют ограниченное сверху (снизу) множество
Бесконечно малой последовательностью называется такая последовательность, что для сколь угодно малой окрестности нуля, вне окрестности будет только счетное число элементов последовательности, а в самой окрестности бесконечное число элементов последовательности.
Бесконечно большой последовательностью называется такая последовательность, что для сколь угодно малой окрестности нуля, вне окрестности будет бесконечное число элементов последовательности , а в самой окрестности только счетное число элементов последовательности.
Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают
Преде́л фу́нкции в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если
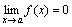 или
или 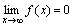 ,
т.е. бесконечно малая функция – это
функция, предел которой в данной точке
равен нулю.
,
т.е. бесконечно малая функция – это
функция, предел которой в данной точке
равен нулю.Предел в точке равен бесконечности
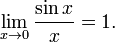
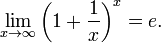
Односторо́нний преде́л — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).
Используя понятие предела, можно сказать, что функция непрерывна в точке х 0 , если в этой точке существует ее предел по множеству Еи этот предел равен
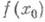 :
:
![]()
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. 1 род: Существуют левосторонний предел
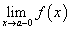 и
правосторонний предел
и
правосторонний предел 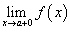 .
Они конечны. Левосторонний
предел и правосторонний предел равны
друг другу – устранимый разрыв, не
равны - конечный
2
род:
Функция f (x) имеет точку
разрыва второго рода при x
= a,
если по крайней мере один из односторонних
пределов не существует или равен
бесконечности.
.
Они конечны. Левосторонний
предел и правосторонний предел равны
друг другу – устранимый разрыв, не
равны - конечный
2
род:
Функция f (x) имеет точку
разрыва второго рода при x
= a,
если по крайней мере один из односторонних
пределов не существует или равен
бесконечности. Пусть в некоторой окрестности точки
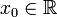 определена функция
определена функция  Производной
функции f в
точке x0 называется предел,
если он существует,
Производной
функции f в
точке x0 называется предел,
если он существует,
![]()
Функция
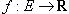 называется дифференцируемой
в точке
называется дифференцируемой
в точке 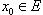 ,
предельной для множества E,
если ее приращение Δf(x0),
соответствующее приращению аргумента x,
может быть представлено в виде Δf(x0)
= A(x0)(x - x0)
+ ω(x - x0), где ω(x - x0)
= о(x - x0)
при x → x0.
,
предельной для множества E,
если ее приращение Δf(x0),
соответствующее приращению аргумента x,
может быть представлено в виде Δf(x0)
= A(x0)(x - x0)
+ ω(x - x0), где ω(x - x0)
= о(x - x0)
при x → x0.Отображение
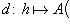
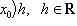 ,
называется дифференциалом функции f в
точке x0,
а величина A(x0)h - значением
дифференциала в
этой точке. Для значения дифференциала
функции f принято
обозначение df или df(x0),
если требуется знать, в какой именно
точке он вычислен. Таким образом, df(x0)
= A(x0)h.
,
называется дифференциалом функции f в
точке x0,
а величина A(x0)h - значением
дифференциала в
этой точке. Для значения дифференциала
функции f принято
обозначение df или df(x0),
если требуется знать, в какой именно
точке он вычислен. Таким образом, df(x0)
= A(x0)h.Теорема о производной сложной функции. Если y(x)=f(u(x)) и существует f’(u) и u’(x), то существует y’(x)=f(u(x))u’(x).
Для дифференцируемой функции с производной, отличной от нуля, производная обратной функции равна обратной величине производной данной функции, т.е
![]()
дифференциал функции у = f(х) в точке хо равен приращению ординаты касательной к графику функции в этой точке, когда хо получает приращение D х
1 Обозначить буквой a абсциссу точки касания. 2. Найти f(a). 3. Найти f '(x) и f '(a). 4. Подставить найденные числа a, f(a), f '(a) в общее уравнение касательной y = f(a) = f '(a)(x – a).
ЭЛАСТИЧНОСТЬ ФУНКЦИИ предел отношения относительного приращения функции y (зависимой переменной)
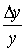 к
относительному приращению независимой
переменной x
к
относительному приращению независимой
переменной x 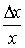 когда
Δx и
Δy→
0 обозначается символом Ex(y)
и выражается следующей формулой:
когда
Δx и
Δy→
0 обозначается символом Ex(y)
и выражается следующей формулой:
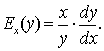
Теорема Лопиталя (раскрытие неопределенности бесконеч/бесконеч) Условия:
 или
или 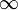 ;
;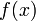 и
и  дифференцируемы
в проколотой окрестности
дифференцируемы
в проколотой окрестности  ;
;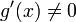 в
проколотой окрестности
;существует
в
проколотой окрестности
;существует 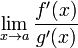 ,тогда
существует
,тогда
существует 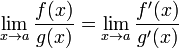 .Пределы
также могут быть односторонними.
.Пределы
также могут быть односторонними.
Производные и дифференциалы высших порядков Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции f и обозначается f". Таким образом, f"(x) = (f'(x))'. Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f(n). Итак, f(n)(x) = (f(n-1)(x))', n ϵ N, f(0)(x) = f(x). Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом, dnf(x) = d(dn-1f(x)), d0f(x) = f(x), n ϵ N. Если x - независимая переменная, то dnf(x) = f(n)(x)(dx)n.
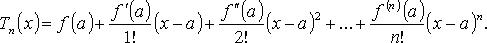 Формула
маклорена – Ф тейлора с а=0
Формула
маклорена – Ф тейлора с а=0Пусть f(x) – дифференцируемая функция на интервале (a,b). Если f‘(x)>0 на (a,b) то на этом интервале функция является монотонно возрастающей.
x0 называется точкой локального максимума функции f, если существует проколотая окрестность
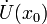 такая,
что
такая,
что
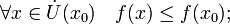
Необходимое условие:Если точка
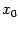 --
это точка локального экстремума
функции
--
это точка локального экстремума
функции 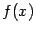 ,
и существует производная в этой точке
,
и существует производная в этой точке 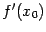 ,
то
,
то  .
.Точка перегиба функции
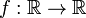 внутренняя
точка x0
области
определения
f,
такая что f
непрерывна в этой точке, существует
конечная или определенного знака
бесконечная производная в этой точке,
и x0
является одновременно концом интервала
строгой выпуклости вверх и началом
интервала строгой выпуклости вниз, или
наоборот. Пусть функция f (x)
непрерывна в точке
внутренняя
точка x0
области
определения
f,
такая что f
непрерывна в этой точке, существует
конечная или определенного знака
бесконечная производная в этой точке,
и x0
является одновременно концом интервала
строгой выпуклости вверх и началом
интервала строгой выпуклости вниз, или
наоборот. Пусть функция f (x)
непрерывна в точке
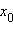 и
имеет в этой точке конечную или
бесконечную производную. Тогда точка
называется
точкой
перегиба
функции f,
если в этой точке изменяется направление
ее выпуклости.
и
имеет в этой точке конечную или
бесконечную производную. Тогда точка
называется
точкой
перегиба
функции f,
если в этой точке изменяется направление
ее выпуклости.Необходимое условие наличия точки перегиба. Если – точка перегиба функции f (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то
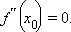
Асимптоты. Определение. Если расстояние от точки M кривой y = f(x) от некоторой прямой y = kx + b стремиться к нулю, когда точка M, двигаясь по кривой, удаляется в бесконечность, то прямая y = kx + b называется асимптотой кривой y = f(x). Асимптоты могут быть вертикальными, наклонными и горизонтальными.
Определение первообразной для ф-ции на промежутке .
Ф-цияy=F(x) называется первообразной для ф-цииy=f(x) на промежутке X, если для любого хϵXвыполняется равенство: F’(x)=f(x)
Определение неопределенного интеграла.Если F(x)-первообразная для f(x), то выражение F(x)+C, где С-произвольная постоянная, называется неопределенным интегралом от ф-цииf(x).(⌠f(x)dx=F(x)+C)
Свойства неопределенного интеграла
Производная неопределенного интеграла равна подфнтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению.
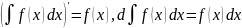
Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная
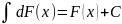
Постоянный множитель можно вынести из-под знака неопределенного интеграла
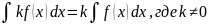
Неопределенный интеграл от суммы функций равен сумме интегралов от слагаемых
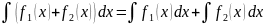
Формула замены переменной в неопределенном интеграле. Пусть ф-цияx=ѱ(t) определена и дифференцируема на промежутке T иX-множество ее значений, на котором определена ф-цияf(x). Тогда если F(x)-первообразная для f(x) на X, то F(ѱ(t))-первообразная для f(ѱ(t)) ѱ’(t)на T, т.е. на множестве T выполняется равенство: ⌠f(x)dx│x=ѱ(t)=⌠f(ѱ(t)) ѱ’(t)dt
Формула интегрирования по частям для неопределенного интеграла.
Пусть u(x) и v(x)-две дифференцируемые ф-ции на промежутке X. Тогда на X выполняется формула интегрирования по частям: ⌠udv=uv-⌠vdu
Интеграла Римана. Ф-цияy=f(x), ограниченная на отрезке [a,b], называется интегрируемой на этом отрезке, если существует единственное число I, разделяющее множества нижних и верхних сумм Дарбу для всевозможных разбиений отрезка [a,b]. Если ф-цияy=f(x) интегрируема на отрезке [a,b], то единственное число, разделяющее эти два множества, называют определенным интегралом ф-цииy=f(x) по отрезку [a,b] и обозначают следующим образом: I=⌠baf(x)dx
Достаточное условие интегрируемости. Для того , чтобы ф-цияy=f(x), определенная и ограниченная на отрезке[a,b], была интегрируемой на этом отрезке, необходимо и достаточно, чтобы для любого e>0, существовало разбиение T, такое, что ST-sT<e
Геометрический смысл определенного интеграла: определенный интеграл равен площади криволинейной трапеции ограниченной линиями x=a,x=b при b>a, осью Ох и графиком неотрицательной непрерывной ф-цииy=f(x)
Свойства определенного интеграла
Интеграл от суммы двух функций f1(x) и f2(x) по отрезку [a;b] равен сумме интегралов от этих функций по тому же отрезку

Постоянный множитель можно выносить из-под знака интеграла
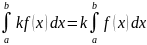
Интеграл от неотрицательной функции на отрезке [a;b] – неотрицательное число, то есть если
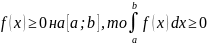
Формула Ньютона - Лейбница.Пусть ф-цияy=f(x) непрерывна на отрезке [a,b] и F(x)-первообразная для f(x). Тогда ⌠baf(x)dx=F(b)-F(a)
Формула замены переменной в определенном интеграле.Пусть ф-цияy=f(x) непрерывна на отрезке [a,b], а ф-ция х=ѱ(t) определена на отрезке[α,β]и имеет непрерывную производную внутри этого отрезка, причем ѱ(α)=a, ѱ(β)=bи ѱ([α,β])=[a,b]. Тогда ⌠baf(x)=⌠βαf(ѱ(t)) ѱ’(t)dt
Формула интегрирования по частям для определенного интеграла.⌠baudv=uv│ba-⌠bavdu
Определение несобственного интеграла с бесконечным верхним пределом.Пусть ф-цияy=f(x) интегрируема на каждом конечном отрезке [a,b] (b>a). Тогда за несобственный интеграл ⌠+∞af(x)dx принимают предел ф-цииI(b)= ⌠baf(x)dx, когда b стремится к бесконечности:⌠+∞af(x)dx=lim⌠baf(x)dx (bк +∞)
Определение несобственного интеграла с бесконечным нижним пределом.Пусть ф-цияy=f(x) интегрируема на каждом конечном отрезке [a,b] (b>a). Тогда за несобственный интеграл ⌠b-∞f(x)dx принимают предел ф-цииI(a)= ⌠baf(x)dx, когда a стремится к бесконечности:⌠b-∞f(x)dx=lim⌠baf(x)dx (aк -∞)
Определение несобственного интеграла от неограниченной функции
