71. Частные производные высших порядков. Частные производные от функций f’x(x,y) и f’y(x,y) называют частными производными второго порядка от ф-цииf(x,y).Частные производные от частных производных второго порядка называют частными производными третьего порядка от ф-ции. Частные производные второго порядка z’’xy и z’’yx называют смешанными частными производными.

72. Теорема о равенстве смешанных производных.Если производные z’’_xyиz’’_yx существуют в некоторой окрестности точки M(x₀,y₀) bи непрерывны в самой точке М, то имеет место равенство z’’_xy=z’’_yx

73. Формула Тейлора для функции нескольких переменных с остаточным членом в форме Лагранжа.

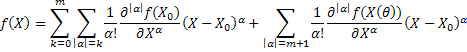
74. Локальные экстремумы функций нескольких переменных.Точка а↑ называется точкой локального максимума (мин) ф-цииf(x↑), если существует такая е-окрестность U_e(a↑)={x↑ϵRⁿ:│x↑-a↑│<e}точки а↑, в которой для любой точки х↑ϵU_e(a↑) выполняется равенство f(x↑)≤f(a↑) (f(x↑)≥f(a↑)). Точки локального максимума и локального минимума называются точками локального экстремума или просто точками экстремума.

75. Необходимое условие локального экстремума функций нескольких переменных.Для того, чтобы дифференцируемая ф-цияf(x↑) имела локальный экстремум точки а↑, необходимо чтобы все ее частные производные первого порядка в этой точке были равны 0. Пусть ф-цияf(x↑) имеет в окрестности точки своего локального экстремума а↑ непрерывные частные производные второго порядка, тогда: если а↑-точка лок мин, то d²f_a↑неотрицат определенная квадрат форма. (для пол наоборот)

76. Достаточное условие локального экстремума функций нескольких переменных.Пусть ф-цияnпеременных f(x↑) имеет в окрестности своей стационарной точки а↑ непрерывные частные производные второго порядка, тогда: если квадр форма d²f_a↑пол определена, то а↑- точка лок мин f (для пол наоборот). Пусть ф-цияf(x,y) имеет непрчастнпроизв второго порядка в некоторой окрестности своей стационарной точки P. Положим ∆=detf’’(P)=f’’_xx(P) f’’_yy(P)-( f’’_xy(P))²тогда если ∆>0, то в точке Рф-ция имеет лок экстремум, при чем f’’_xx(P)<0-лок макс, f’’_xx(P)>0- лок мин; если ∆<0, то в точке Р нет экстремума

77. Условный экстремум.Точка х*↑ϵХ называется точкой условного локального максимума (мин) ф-цииf, если для всех достаточно близких к ней точек х↑ϵХ выполняется неравенство: f(x↑)≤ f(x*↑) f(x↑)≥f(x*↑)- точки условного экстремума

78. Метод Лагранжа: Дано: f(x,y) и g(x,y).

1) L(x,y,λ)= f(x,y)+λg(x,y).

2 ) dL/dx=0

dL/dу=0 из этого находим стационарную точку (х*; у*)

dL/dλ=0

3) а) Если (х*; у*) - единственная стационарная точка, то нужно взять произвольную точку (х₁; у₁), удовлетворяющую соотношению g(x₁;y₁)=0 и вычислить f(x*;y*) иf(х₁; у₁) и сравнить между собой, далее сделать выводЕсли(х*; у*) - maxили min

б) Если несколько стационарных точек, тогда нужно вычислить значение ф-цииfв этих точках и сделать вывод, кто min, ктоmax.

79. Наибольшее и наименьшее значения непрерывной функции на замкнутом ограниченном множестве. Дифференциальнаяф-ция на ограниченном и замкнутом множестве может принимать наименьшее и наибольшее значение, либо в критических точках внутри этого множества, либо на границе этого множества.

80. Кратные интегралы и их свойства. Условия интегрируемости функции.

Кратным (n-кратным) интегралом функции   на множестве   называется число   (если оно существует), такое что, какой бы малой  -окрестностью числа   мы ни задались, всегда найдется такое разбиение множества   и набор промежуточных точек, что сумма произведений значения функции в промежуточной точке разбиения на меру разбиения будет попадать в эту окрестность. Формально:

 :   : 

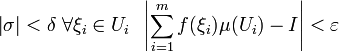
Свойства кратных интегралов

Линейность по функции. Пусть   измеримо, функции   и   интегрируемы на  , тогда

.

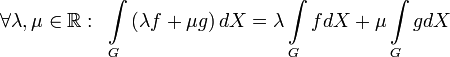Аддитивность по множеству интегрирования. Пусть множества   и   измеримы,   и  . Пусть также функция   определена и интегрируема на каждом из множеств   и  . Тогда интеграл по   существует и равен

.

Монотонность по функции. Пусть   измеримо, функции   и   интегрируемы на  , причем  . Тогда

.

Интегральное неравенство треугольника. Следствие предыдущего свойства.

Интегральная теорема о среднем. Пусть   — компакт, функция   непрерывна и интегрируема на  , тогда

Постоянная функция   интегрируема на любом измеримом множестве  , причем

.

Как следствие,  .

Достаточные условия

Если функция непрерывна на измеримом по Жордану компакте, то она интегрируема на нем.

Неограниченная функция на множестве может быть не интегрируемой, даже если она непрерывна. Например, функция   не интегрируема на интервале  .

Если функция определена на измеримом по Жордану множестве, у которого существуют сколь угодно мелкие разбиения, для которых данная функция неограничена на объединении всех их элементов положительной меры, то эта функция неинтегрируема на этом множестве.

81. Сведение кратного интеграла к повторному: если ф-цияf(x,y) интегрируема в области G и при любом фиксированном xиз [a,b] существует интеграл ⌠_g1(x)^g2(x)f(x,y)dxdy=⌠^b_a{⌠_g1(x)^g2(x)f(x,y)dy}dx

82. Формула замены переменных в двойном интеграле. Использование полярных координат для вычисления двойных интегралов.

Переход к полярным координатам:

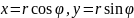
83. Геометрические приложения двойных интегралов: вычисление площадей плоских фигур и объемов пространственных тел.

Двойной интеграл представляет собой объем прямого цилиндрического тела, ограниченного снизу областью D, а сверху- поверхностью z=f(x,y)

Если подынтегральнгая функция f(х,y) тождественно равна единице в области D, то значение двойного интеграла совпадает с площадью области интегрирования

84. Несобственные кратные интегралы. Интеграл Эйлера-Пуассона.

85. Числовые ряды

Пусть дана числовая последовательность a1, a2, a3, … , an, … Выражение вида a1+a2+a3+….+an+…= называют числовым рядом, или просто рядом

86. Последовательность частичных сумм. Сумма ряда. Сходящиеся ряды.

Суммы конечного числа первых членов ряда S₁=a₁, S2=a1+a2, S3=a1+a2+a3, …, Sn=a1+a2+a3+…+an, называют частичными суммами ряда. Так как число членов ряда бесконечно, то частичные суммы образуют числовую последовательность S1,S2,S3,...,Sn.

Ряд называют сходящимся, если последовательность его частичных сумм сходится к некоторому числу S. В этом случае число S называют суммой ряда.

87. Свойства сходящихся рядов

1. Если сходится ряд а1+а2+а3+….+аn+…, то сходится любой ряд, полученный из него отбрасыванием конечного числа членов

2. Если ряд а1+а2+а3+….+аn+… сходится и его сумма равна S, а с – некоторое число, то сходится ряд са1+са2+са3+…+саn+… и его сумма равна сS

3. Если оба ряда а1+а2+а3+….+аn+… и b1+b2+b3+…+bn+… сходятся, а их суммы равны соответсвенно S и T, то и ряд (a1+b1)+(a2+b2)+(a3+b3)+…+(an+bn)+… сходится и его сумма равна S+T

4. Если сходится ряд а1+а2+а3+….+аn+…, то сходится и любой ряд, полученный из него группировкой слагаемых, причем суммы обоих рядов одинаковы.

88. Необходимое условие сходимости ряда. Если ряд сходится, то предел его общего члена равен нулю. Док – во. Пусть данный ряд сходится и его сумма равна S. Для любого натурального n имеем S_n=S_n-1+a_n, или a_n=S_n-S_n-1. При n→∞ обе части суммы S_n иS_n-1 стремятся к пределу S_, поэтому из равенства a_n=S_n-S_n-1 следует, что lim_n→∞a_n= lim_n→∞S_n- lim_n→∞S_n-1=S-S=0. Подчеркиваем еще раз, что мы установили, только необходимое условие сходимости ряда, т.е. условие при на рушении которого ряд не сможет сходиться. С помощью этого признака можно доказывать только расходимость ряда.

89. Числовые ряды с неотрицательными членами. Числовой ряд называется рядом с положительными членами, если общий член ряда ап >0 для любого n=1,2,....Для того чтобы ряд с положительными членами сходился, необходимо и достаточно, чтобы послед-ть его частичных сумм была ограничена.

90. Критерий сходимости числовых рядов с неотрицательными членами. Для того чтобы ряд с положительными членами сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.

91. Признаки сравнения, Даламбера и Коши: Если для ряда с положительными членами a₁+a₂+….+a_n+…. Существует такое число q<1, что при всех n(или, начиная с некоторого n ) выполняется неравенство a_n+1/a_n<q, то ряд сходится. Если же a_n+1/a_n>1 для всех или начиная с некоторогоn,то ряд расходится.

Признак Коши: Если существует предел lim_n→∞a_n+1/a_n=d, то ряд сходится в случае d<1, расходится в случае d>1.

Интегральный признак: Пусть неотрицательная ф-цияy=f(x) определена и монотонно убывает для x>1. Тогда для сходимости ряда f(1)+f(2)+…+f(n)+… необходимо и достаточно, чтобы сходился несобственный интеграл ∫₁^∞f(x)dx

Первый признак сравнения: Пусть даны два ряда с положительными членами: a₁+a₂+….+a_n+…. И b₁+b₂+….+b_n+…., причем члены первого ряда не превосходят соответствующих членов второго: a_n<b_n (n= 1, 2,….). Тогда из сходимости второго ряда («большего») следует сходимость первого ряда («меньшего»). Эквивалентно из расходимости меньшего ряда следует расходимость большего ряда.

Второй признак сравнения: Если для рядов a₁+a₂+….+a_n+…. И b₁+b₂+….+b_n+….,с положительными членами существуют отличный от нуля предел отношения limn→∞a_n/b_n=u, то ряды a₁+a₂+….+a_n+…. И b₁+b₂+….+b_n+…. Сходятся или расходятся одновременно.

92. Знакопеременные ряды. Абсолютная и условная сходимость .Особенно часто среди знакопеременных рядов встречаются ряды члены которых имеют чередующиеся знаки, т.е. знакочередующиеся ряды. Знакочередующийся ряд в общем виде записывается так: а₁-а₂+а₃-а₄+….+(-1)^п-1а_п+…, где а_п – положительны. Ряд a₁+a₂+….+a_n+…. Называют, условно сходящимся, если он сходится, а ряд составленный из модулей его членов, расходится. Абсолютно сходящийся ряд, т.е. такой, для которого ряд из модулей его членов сходится.

93. Признак Лейбница для знакочередующихся числовых рядов . Если члены знакочередующегося ряда убывают по абсолютной величине и стремятся к нулю, когда n→∞, то 1) ряд сходится 2) любой остаток ряда не превосходит по абсолютной величине первого из своих членов и имеет одинаковый с ним знак.

94. Степенные ряды. Ряд вида a₀+a₁x+a₂x+…+a_nx_n+…, гдеa₀, a₁, a₂, …,a_n, … - некоторая числовая послед-ть, называют степенным рядом.

95. Теорема Абеля.Если степенной ряд a₀+a₁x+a₂x+…+a_nx_n+… сходится при некотором х=х₀, не равном нулю, то он сходится, и притом абсолютно, при всех х, удовлетворяющих условию |х|<|x₀|; Если ряд a₀+a₁x+a₂x+…+a_nx_n+… расходится при некотором х=х₁, то он расходится при всех х, удовлетворяющих условию |х|>|x₁|

96. Интервал и радиус сходимости степенного ряда.Теорема: Для степенного ряда a₀+a₁x+a₂x+…+a_nx_n+… возможны только три случая: 1) ряд сходится только в единственной точке х=0; 2) ряд сходится для всех значений х; 3) существует такое R>0, что ряд сходится для всех значений х из интервала (-R;R) и расходится для всех значений х вне отрезка [-R;R].Определение: интервал (-R;R) называют интервалом сходимости ряда a₀+a₁x+a₂x+…+a_nx_n+…, число R –радиусом сходимости этого ряда.

97. Интегрируемость и дифференцируемость суммы степенного рядана интервале сходимости. Пусть ф-ция разлагается на интервале (-R;R) в степенной ряд f(x)=a₀+ a₁x+ a₂x²+..+ a_nxⁿ+..(1)Рассмотрим степенной ряд a₁+ 2a₂x+..+na_nx^n-1+..(2) полученный почленным дифференцированием ряда:

1)ряд (2) имеет тот же радиус сходимости R, что и ряд (1)

2) на всем интервале (-R,R) ф-цияf(x) имеет производную f’(x), которая разлагается в степенной ряд (2)

Следствие: ф-цияf(x) , которая разлагается в степенной ряд (1)на интервале (-R,R), бесконечно диф на этом интервале. Разложение в степенной ряд для любой производной получается почленным дифференцированием ряда (1). При этом радиусы сходимости рядов раны радиусу сходимости ряда.

Если ф-цияf(x) разлагается в степенной ряд на интервале (-R,R), то она интегрируема на этом интервале. Интеграл от суммы ряда равен сумме интегралов от членов ряда: ⌠^x2_x1f(x)dx=⌠^x2_x1a₀+ a₁x+ a₂x²+..+ a_nxⁿ+.dx=⌠^x2_x1 a₀+⌠^x2_x1 a₂ x²dx+…⌠^x2_x1 a_nxⁿdx+..