49. На ограниченном промежутке

Пусть функция y=f(x)не ограничена на отрезке [a;b], однако интегрируема на любом меньшем отрезке [a;b-ɛ], где ɛ>0. Тогда если существует предел 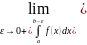, его принимают за несобственный интеграл от неограниченной функции f(x):

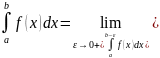
50. Расстояние в . Свойства расстояния.В R¹:расстояние между точками x₁иx₂ равно │x₁ –x₂│

R²:P(x₁,y₁) иQ(x₂,y₂), то ρ(P,Q)=√( y₁ - x₁)²+( y₂ –x₂)²)

R³: P(x₁,y₁,z₁) иQ(x₂,y₂,z₂), тоρ(P,Q)=√( x₁ –x₂)²+( y₁– y₂)²+(( z₁– z₂)²)

Rⁿ: ρ(p,q)=│p-q│=√( x’₁ –x’’₁)²+…+( x’_n– x’’_n)²)

Свойства: Ρ(p,q)>0, если p≠qи ρ(p,p)=0; Ρ(p,q)=Ρ(q,p); Ρ(p,q)+Ρ(q,r)≥ Ρ(p,r)

51. Окрестность точки в .Пусть p₀- точка в Rⁿи е-положительное число. Открытым шаром, или просто шаром радиуса е с центром p₀называется множество всех точек, расстояние которых от p₀меньше е:{pϵRⁿ│ρ(p₀,p)<e}. Шар радиуса e с центром p₀, обозначаетсяB(p₀,e) или U(p₀). Множество U_e(p₀) называют e-окрестностью точки p₀

52. Открытые и замкнутые множества.МножествоD называется открытым, если все его точки внутренние (замкнутым, если оно содержит все свои граничные точки).Множество {M} называется замкнутым, если все граничащие точки принадлежат этому множеству.

53. Изолированные и предельные точки множества.Точка М₀ называется предельной точкой множества {M}, если в любой ее окрестности существуют точки множества {M}, отличные от М₀. Точка p₀ ϵХ называется изолированной точкой множества Х, если у нее существует е-окрестность, в которой никаких других точек из Х кроме p₀, нет.

54. Ограниченные множества.Множество XϵRⁿ называется ограниченным, если оно целиком содержится в некотором шаре. (Пусть p₀- точка в Rⁿи е-положительное число. Открытым шаром, или просто шаром радиуса е с центром p₀называется множество всех точек, расстояние которых от p₀меньше е:{pϵRⁿ│ρ(p₀,p)<e}.)

55. Сходимость последовательности точек в Rⁿ, ее эквивалентность покоординатной сходимости.Пусть {p_n}- послед-ть точек в Rⁿ. Эта послед-ть сходится к точке p_o, если числовая послед-ть {ρ(p_n,p₀)} имеет предел 0.Пусть p₁=(x₁,y₁), p₂=(x₂,y₂),…-послед-ть точек в R². Мы скажем, что эта послед-ть сходится к точке p0=(x₀,y₀), если числовая послед-тьx₁,x₂,… сходится к числу x₀, а числовая послед-тьy₁,y₂,…- к числу y₀.

56. Функция нескольких переменных

Числовая функция n переменных характеризуется тем, что областью ее определения является подмножетсво X пространства Rⁿ, n>1. В этом случае значение аргумента х представляет собой точку (х1, х2, … , хn) из Rⁿ; соответсвенно пишут: y=f(x1, X2, …, xn)

57. Поверхности (линии) уровня функции нескольких переменных.

Линией уровня функции f(x,y) называют линию f(x.y)=C на координатной плоскости, в точках которой функция f принимает постоянное значение С.