28. Формула Тейлора. Формула Маклорена.

теорема Тейлора.

Пусть функция f(x) имеет в точке x = a и некоторой ее окрестности производные порядка n+1. Тогда между точками a и x a найдется такая точка , что справедлива следующая формула:

Формула (10) называется формулой Тейлора, а выражение

представляет остаточный член в форме Лагранжа. Заметим, что если функция f⁽ⁿ⁺¹⁾(x) ограничена в окрестности точки a, тогда остаточный член является бесконечно малой при x a более высокого порядка, чем (x-a)ⁿ. Таким образом, остаточный член можно записать в виде

R_n+1(x) = o((x-a)ⁿ) при x a.

Данная форма записи остаточного члена называется формой Пеано.

Формулой Маклорена называется формула Тейлора при a = 0:

Остаточный член в форме Пеано для формулы Маклорена имеет вид

R_n+1 = o(xⁿ) при x 0.

П риведем разложения некоторых элементарных функций по формуле Маклорена

29. признак монотонности дифференцируемой функции:

Промежутки монотонности ф-ции совпадают с промежутками постоянного знака её производной

30. определение локального экстремума функции одной переменной:

Точка x₀ называется точкой локального max [min] ф-ции f(x), если для всех x из некоторой окрестности точки x₀ выполняется неравенство

Локальный max и min объединяются общим названием локальны экстремум.

31. необходимое условие локального экстремума функции одной переменной:

Для того, чтобы дифференцируемая ф-ция f(x) имела в точке x₀ локальный экстремум необходимо, чтобы в этой точке выполнялось равенство . Если при переходе через точку х0 меняет знак с + на – (с – на +), то х0 – это локальный максимум (минимум).

.

32. точка перегиба функции:

пусть функция f(x) непрерывна в точке х0. Точка х0 называется точкой перегиба, если при переходе через нее кривая меняет направление выпуклости .

33. необходимое условие точки перегиба:

пусть функция f(x) непрерывна в точке х0. Точка х0 называется точкой перегиба, если при переходе через нее кривая меняет направление выпуклости ( слева и справа от х0 знаки второй производной различны)

34. определение асимптот графика функций:

Асимптота графика функций y=f(x) - это прямая, расстояние до которой от точки (x,y) графика функций y=f(x) стремится к нулю, если хотя бы одна из координат (x,y) стремится к бесконечности. Асимптоты бывают вертикальными, наклонными и горизонтальными.

35. определение первообразной для функций y=f(x) на промежутке X:

Пусть задана функция f(x) на интервале (a,b) . функция F(x) называется первообразной для функции f(x) на интервале (a,b), если F`(x)= f(x)для всех x принадлежащих (a,b).

36. определение неопределенного интеграла:

Совокупность всех первообразных функций f(x) называется неопределенным интегралом и обозначается (« интеграл эф от икс дэ икс»).

37. свойства неопределенного интеграла:

38.Формула замены переменной в неопределенном интеграле.

Если интеграл нельзя найти непосредственно, то в некоторых случаях можно применить метод замены переменной, положив х=ф(t), где ф(t)- непрерывно дифференцируемая монотонная функция. Справедливая формула замены переменной:

39.Формула интегрирования по частям для неопределенного интеграла.

Пусть u(x) и v(x) – две дифференцируемые функции на промежутке Х. Тогда на Х выполняется формула интегрирования по частям

40.Определение определенного интеграла Римана.

Если функция y=f(x) интегрируема на отрезке [a;b], то единственное число, разделяющее эти два множества называют определенным интегралом функции y=f(x) по отрезку[a;b] и обозначают следующим образом:

41. Достаточное условие интегрируемости.

Функция y=f(x) называется интегрируемой на этом отрезке, если существует единственное число I, разделяющее множества нижних и верхних сумм Дарбу для всевозможных разбиений отрезка [a;b].

42. Геометрический смысл определенного интеграла: определенный интеграл равен площади криволинейной трапеции ограниченной линиями x=a,x=b при b>a, осью Ох и графиком неотрицательной непрерывной ф-цииy=f(x)

43.Свойства определенного интеграла.

1) . 2)

_{3) 4)} ,для любых a,b,c. 5)Если f(x)≤g(x) отрезке [a,b], то 6)Если на отрезки [a,b] выполняется неравенства 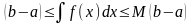₍оценка интеграла). 7)Теорема о среднем. Для непрерывной на отрезке[a,b] функция y=f(x) найдется точка С принадлежащая [a,b],что _.

44. Формула Ньютона-Лейбница.

Для нахождения определенного интеграла для функции f(x), интегрируемой на отрезке[a,b]: , гдеF(x)- любая первообразная для функции f(x) на[a,b].

45.Формула замены переменной в определенном интеграле.

Пусть в определенном интеграле _с непрерывной подынтегральной функцией f(x) производят замену переменной x= (t), при чем функция (t) непрерывно дифференцируема на отрезке [ ] и тогда справедливо равенство (t)dt.

46.Формула интегрирование по частям для определенного интеграла.

Пусть u(x) и v(x)-две непрерывно дифференцируемые функции на отрезке [a,b]. Тогда выполняется формула интегрирования по частям _│

47. Определение несобственного интеграла с бесконечно верхним пределом.

Если существует конечный предел 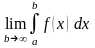_, то этот предел называется несобственным интегралом с бесконечно верхним пределом пределом от функции f(x) и обозначается _.

48.Определение несобственного интеграла с бесконечно нижним пределом.

Если существует конечный предел _, то этот предел называется несобственным интегралом с бесконечно нижним пределом от функции f(x) _и обозначается _.

49.Определение несобственного интеграла от неограниченной функции на ограниченном промежутке.

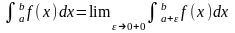Если функция f(x) определена при , интегрируема на любом отрезке и не ограничена слева от точки b, то по определению полагают Аналогично, если функция f(x) не ограничена справа от точки а, то . Наконец, если функция в окрестности внутренней точки с отрезка [a,b]не ограничена, то по определению _.

50. Расстояние в Rⁿ. Свойства расстояния.

В пространстве Rⁿ, где n>3 , о расстоянии можно говорить лишь в условном смысле, так как точки в Rⁿ не имеют непосредственного геометрического истолкования. Расстояние определяется формулой:

ρ (p,q)= │p-q│=√(x1’- x1”)²+…+(xⁿ’-xⁿ”)²

, где p=(x1’, x2’, …, xⁿ’) и q=( x1”, x2”, …, xⁿ”) – две произвольные точки из Rⁿ.

Свойства:

1) ρ (p,q)>0, елси p ≠ q, и ρ (p,p)=0;

2) ρ (p,q)= ρ (q,p);

3) ρ (p,q)+ ρ (q,r)>= ρ (p,r), каковы бы ни были точки p,q и r. (свойство треугольника).