
- •2. Понятие обратной функции.
- •4. Определение предела последовательности.
- •6. Определение ограниченной последовательности.
- •21.Теорема о производной сложной функции.
- •22.Теорема о производной обратной функции.
- •23. Геометрический смысл производной и дифференциала.
- •28. Формула Тейлора. Формула Маклорена.
- •51. Окрестность точки в rⁿ.
- •52. Открытые и замкнутые множества.
- •53. Изолированные и предельные точки множества.
- •55. Сходимость последовательности точек в Rn, ее эквивалентность покоординатной сходимости.
- •72. Теорема о равенстве смешанных производных
- •73. Формула Тейлора для функции нескольких переменных с остаточным членом в форме Лагранжа.
- •74. Локальные экстремумы функций
- •75. Необходимое условие локального экстремума функций нескольких переменных.
- •76. Достаточное условие локального экстремума функций нескольких переменных.
- •77. Условный экстремум.
- •78. Метод Лагранжа.
- •79. Наибольшее и наименьшее значения непрерывной функции на замкнутом ограниченном множестве.
- •86. Последовательность частичных сумм. Сумма ряда. Сходящиеся ряды.
- •87. Свойства сходящихся рядов.
- •88. Необходимое условие сходимости числового ряда.
- •89. Числовые ряды с неотрицательными членами.
- •90. Критерий сходимости числовых рядов с неотрицательными членами.
- •91. Признаки сравнения, признак Даламбера и Коши, интегральный признак для числовых рядов с неотрицательными членами.
- •92. Знакопеременные ряды. Абсолютная и условная сходимость.
- •93. Признак Лейбница для знакочередующихся числовых рядов.
- •109. Общее решение однородной системы линейных
72. Теорема о равенстве смешанных производных
Если
производные
 и
и
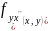 существуют в некоторой окрестности
точки М(х0,
у0)
и непрерывны в самой точке М,
то
имеет место равенство
существуют в некоторой окрестности
точки М(х0,
у0)
и непрерывны в самой точке М,
то
имеет место равенство
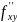 (М)=(М)
(М)=(М)
73. Формула Тейлора для функции нескольких переменных с остаточным членом в форме Лагранжа.
Пусть
функция f(х)
имеет (п +1)
производных
в E-окрестности
точки х0
. Тогда для
любой точки х из этой окрестности
найдется точка с, расположенная между
точками х и х0,
для которой выполняется следующая
формулаf(х)
= T(х)
+
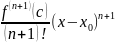
где T(x)- п-й многочлен Тейлора функции f(х) в точке х0. - остаточный член в форме Лагранжа
74. Локальные экстремумы функций
нескольких переменных.
Точка М называется точкой локального минимума функции у=f(x), если существует такая окрестность М, что в любой точке Xэтой окрестности выполняется неравенство f(М) <= f(X).
Аналогично точка М называется точкой локального максимума функции y = f (X), если существует такая окрестность М, что в любой точке X этой окрестности выполняется неравенство f(М) >= f(X).
Точки локальных минимумов и максимумов функции у=f(X) называются точками локальных экстремумов данной функции
75. Необходимое условие локального экстремума функций нескольких переменных.
Теорема.
Пусть функция f(x1,
..., xm)
определена в некоторой окрестности т.
![]() ,
дифференцируема в точке М0,
и имеет в этой точке локальный экстремум,
тогда все частные производные первого
порядка функции f в т. М0
равны нулю:
,
дифференцируема в точке М0,
и имеет в этой точке локальный экстремум,
тогда все частные производные первого
порядка функции f в т. М0
равны нулю:
![]()
76. Достаточное условие локального экстремума функций нескольких переменных.
Пусть в некоторой окрестности стационарной точки определены частные производные второго порядка функции f(x1, ..., xm), которые являются непрерывными в т. М0. Если в этой точке второй дифференциал d2 f(M0) является знакоопределенной квадратичной формой от dx1, ..., dxm, то в т. М0 функция имеет локальный экстремум (локальный максимум, если d2 f(M0) отрицательно определена, и локальный минимум, если d2 f(M0) положительно определена), если же d2 f(M0) знакопеременна, то в т. М0 экстремума нет.
77. Условный экстремум.
Пусть у= f(X) функция с областью определения D(f) и пусть S - подмножество в D(f) (т.е. S является частью в D(f). Точка Aпринадлежит S называется точкой условного минимума функции f, если существует такая окрестность точки А, что для любой точки В, лежащей одновременно и в этой окрестности точки А и множестве S, верно неравенство f(A)<= f(B).
Аналогично точка А принадлежит S называется точкой условного максимума функции f, если существует такая окрестность точки А, что для любой точки В, лежащей в этой окрестности и в S, верно неравенство f(A)>=f(B).
Общее название для условных минимумов и максимумов — условные экстремумы.
78. Метод Лагранжа.
Пусть функции f и g1 …gs определены и имеют непрерывные частные производные в окрестности точки х* причем, векторы
![]()
линейно
независимы. Тогда если х* - точка условного
экстремума функции f
при условиях
![]()
то найдутся числа ʎ1 …ʎs для которых x* - стационарная точка функции
![]()
Функция L называется функцией Лагранжа, а числа множителями Лагранжа.
