79. Наибольшее и наименьшее значения непрерывной функции на замкнутом ограниченном множестве.

Множество S называется ограниченным, если оно содержится внутри круга (для множества на плоскости) или внутри шара (для множества в пространстве), имеющего достаточно большой радиус. Множество называется замкнутым, если оно включает в себя все свои предельные точки.

Важным свойством непрерывных функций является следующее.

Пусть z= f(x,у) — непрерывная функция, a S — замкнутое и огра­ниченное множество, лежащее в области определения функции f. Тогда в S существуют точки, в которых функция принимает свои наиболь­шее и наименьшее значения, множество значений представляет собою отрезок [f_наим,f_наиб].

80. Кратные интегралы и их свойства. Условия интегрируемости функции.

Определение. Если существует конечный предел интегральных сумм при ʎ->0 то функция f(x;y) называется интегрируемой в области D. Значение этого предела называется двойным интегра­лом по области D X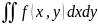

81. Сведение кратного интеграла к повторному интегралу.

Если функция f(x,y) интегрируема в области G и при любом фиксированном х из [а,b] существует интеграл 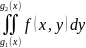справедлива формула

82. Формула замены переменных в двойном интеграле. Использование полярных координат для вычисления двойных интегралов.

В полярных координатах :

83. Геометрические приложения двойных интегралов: вычисление площадей плоских фигур и объемов пространственных тел.

Определение. Если существует конечный предел интегральных сумм при ʎ->0 то функция f(x;y) называется интегрируемой в области D. Значение этого предела называется двойным интегра­лом по области D

84. Несобственные кратные интегралы. Интеграл Эйлера-Пуассона.

Пусть GсR² — неограниченное множество, f(x, у) - функция, интегрируемая по всякому подмножеству в G вида G∩D, где D - ограниченное множество с границей нулевой площади. Если для любого допустимого семейства {D_t} предел

существует и не зависит от выбора семейства {D_t}, то данный предел обозначается G и называется несобственным двойным интегралом от f по G.

85. Числовые ряды.

Определение. Пусть дана числовая последовательность а₁ ,а₂, а₃….a_n . Выражение вида

называют числовым рядом, или просто рядом.

Числа а₁ ,а₂, а₃,….a_n называют членами ряда, число а_п с общим номером п называют общим членом ряда.

Суммы конечного числа первых членов ряда

называют частичными суммами ряда. Так как число членов ряда бесконечно, то частичные суммы образуют числовую последовательность

86. Последовательность частичных сумм. Сумма ряда. Сходящиеся ряды.

Пусть дана некоторая последовательность действительных чисел а_п. Тогда сумма бесконечного числа членов этой последовательности

называется числовым рядом, а число а_п (n = 1,2,...) — членом ряда. Если член ряда а_п представлен в виде функции, натурального аргумента а_п= f (п), то его называют общим членом ряда. При этом сумму S_n = а₁+ а₂ +...+ а_п первых п членов ряда называют его n-ой частичной суммой. Таким образом, мы можем образовать новую последователь­ность - последовательность частичных сумм S₁=a₁, S₂=a₁+a₂, S₃=a₁+a₂+a₃, S_n =a₁+ a₂ +...+a_n . Если эта последовательность имеет конечный предел S = lim S_n при n->infimity, то числовой ряд называется сходящимся, а число S — суммой ряда. В противном случае ряд называ­ют расходящимся.