17. Динамические модели с распределёнными лагами.

При анализе многих экономических показателей (особенно в макроэкономике) часто используются ежегодные, ежеквартальные, ежемесячные и ежедневные данные. В этом случае следует упорядочить данные по времени их получения и построить так называемые временные ряды.

Модели, у которых в качестве объясняющих переменных используются не только текущие значения переменных, но и некоторые предыдущие по времени значения, а также само время T, носят названия динамических.

Обычно динамические модели подразделяют на 2 класса: 1)модели с распределёнными лагами; 2) авторегрессионные модели.

Модели с распределёнными лагами. Лаговые переменные – переменные, влияние которых характеризуется определённым запаздыванием. Это модели, содержащие в качестве лаговых переменных лишь независимые переменные:

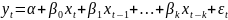
Авторегрессионные модели – это модели, уравнения которых в качестве лаговых объясняющих переменных включают значения зависимых переменных:

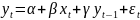
Оценка модели с распределёнными лагами во многом зависит от того, конечное или бесконечное число лагов она содержит.

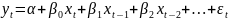
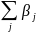В обеих моделях коэффициент называют краткосрочным мультипликатором, так как он характеризует изменение среднего значения Y под воздействием единичного изменения переменной X в тот же самый момент времени. Сумму всех коэффициентов называют долгосрочным мультипликатором. А любую сумму коэффициентов 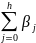(h<k) называют промежуточным мультипликатором. Модель с конечным числом лагов оценивается достаточно просто сведением её к уравнению множественнойрегрессии. В этом случае полагают 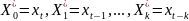и получают уравнение:

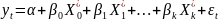
Для оценки моделей с бесконечным числом лагов разработано несколько методов: 1) метод последовательного увеличения количества лагов; 2) преобразование Койка (метод геометрической прогрессии).

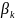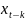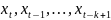1) по данному методу уравнения рекомендуется оценивать с последовательно увеличивающимся количеством лагов. Признаков завершения процедуры увеличения количества лагов может быть несколько: а) при добавлении нового лага какой-либо коэффициент регрессии при переменной меняет знак. Тогда в уравнении регрессии оставляют переменные , коэффициенты при которых знак не поменяли; б) при добавлении нового лага коэффициент регрессии при переменной становится статически незначимым. Очевидно, что в уравнении будут использоваться только переменные , коэффициенты при которых остаются статически значимыми.

2) В распределении Койка предполагается, что коэффициенты («веса») при лаговых значениях объясняющей переменной убывают в геометрической прогрессии:

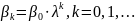
где 0 <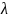 < 1 характеризует скорость убывания коэффициентов с увеличением лага (с удалением от момента анализа). В данном случае уравнение

преобразуется в уравнение вида:

Параметры данного уравнения 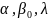можно определить различными способами.

18. Структура лагов по Койку: Частные случаи (модель с неполной корректировкой и адаптивных ожиданий)

Эндогенные иэкзогенные переменные редко включаются в модель в один и тот же моментвремени. Решения, которые должны принять участники экономики, требуют t, необходимого для их воплощения в жизнь. ЭМ в которой экзогенные переменные входят с учетом запаздывания во времени, носят названия лаговых.

МЛР с запаздывающей во времени экзогенной переменной

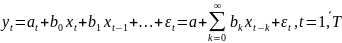
Для физической реализуемости динамической модели требуется выполнение условия сходимости следующего ряда: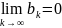 . На практике применяется модель с конечным числом запаздываний, являющаяся частным случаем предыдущей.

1) Геометрическая лаговая структура (Койка). Пусть все параметры b_kубывают с ростом k по геометрической прогрессии со знаменателем q(0<q<1)

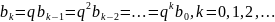
Тогда рассмотренная модель примет упрощенный вид:

.

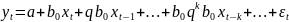Окончательно нормализованный вид модели:

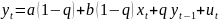
В этой модели необходимо оценить лишь три неизвестных параметра (a,b и q) вместо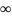 , но => появление сериальной корреляции случайной переменной u_t. Тесты проверки на сериальную корреляцию: Тест h-Дарбина и Множественный критерий Лагранжа.

^{Модель адаптивных ожиданий.}

Обозначим через 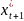ожидаемое (в момент t) будущее значение переменной x_t. Значение величины y_tопр этим ожидаемым значением:

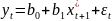(1) – долгосрочная ф-я адаптивных ожиданий

Гипотеза адаптивных ожиданий предпо­лагает, что ожидания пересматриваются в некоторой пропорции от разницы между наблюденным знач и про­гнозом переменной х на предыдущем шаге: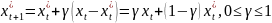 (2)

Если ү=0, то ситуация не изменится, если 1 - ситуация будет близка к прогнозной. Напр. фирма при­нимает решение об V производимой в период tпродукции y_tдо того, как известна цена x_t+1. Поскольку цена x_t+1не из­вестна в период t, то решение принимается на основе ожидаемого значения –яв-сявзвеш средним наблюдаемой цены х и ожидаемой цены х* в период t.

Если выразить через x_tиз (2), введя оператор запаздывания:

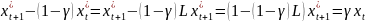
и подставив в (1)

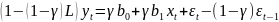или

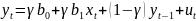
Эта модель (краткосрочная ф-я адаптивных ожиданий) совпадает с моделью Койка. Модель включает только фактические знач переменных, поэтому их можно определить с помощью стандартных стат методов.

Модель с неполной корректировкой.

В отличие от пред модели эмпирически ненаблюдаемой переменной яв-ся результативный признак. Общий вид этой модели сле­дующий:

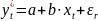(3) долгосрочная ф-я неполной корректировки

Формирование ожиданий экономических агентов относи­тельно значений 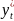происходит по следующей схеме:

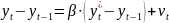, где .

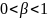В этой модели предполагается, что абсолютное изменение фактических уровней результата есть некоторая доля его ожидае­мого абсолютного изменения. Параметр этой модели называ­ют корректирующим коэффициентом. Чем ближе величина к 1, тем в большей степени реальная динамика показателя отвечает ожиданиям экономических агентов. Чем ближе к 0, тем менее реальное изменение показателя соответствует его ожидаемому изменению. При = 0 значение результативного признака явля­ется константой, на которую ожидания агентов не оказывают ни­какого воздействия.Запишем гипотезу о формировании у' в виде:

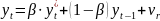(4) где фактическое знач результата текущего периода.

Подставим уравнение (3) в (4). Получим:

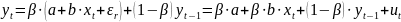(5)где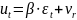

Соотношение (5) есть основное уравнение модели непол­ной корректировки. Его называют краткосрочной функцией мо­дели. Включает только фактические значения переменных. Зная оцен­ки параметров этого уравнения, можно найти . Затем найти a, b.