2.Простая линейная регрессия. Классические предположения модели.
Простая линейная регрессия (ПЛР) – y = f(x; a) + ε;
у – эндогенная, х – экзогенная, ε – случайная «шоковая» переменная, а – неизвестный вектор параметров модели.
ε – случайные погрешности модели, а также экз. (факторные) пер-ные, кот. считаются несущественными по степени влияния на энд.пер-ную.
Пример: Y=ax+b+ε; x–уровень безработицы, y–темп инфляции.
По степени владения априорной информацией различ. 2 задачи:
1)при неизвестной функции взаимосвязи – задача подбора структуры модели.
2)при заданной функции – задача оценивания неизвестных параметров. Основной метод оценивания параметров – метод наименьших квадратов, кот.обеспечивает оптимальные свойства оценкам только при выполнении классических предположений:
П1.
отсутствие систематич.ошибок наблюдений
уравнения регрессии: M{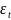
}
= 0, t=1,…,T.(случайные
перем не влияют)
П2.
случайные ошибки некоррелированы между
собой: M{
*
}
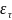= 0, t
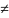τ,
t,τ=1,…,T.
П3.
наблюдения производятся с одинаковой
точностью, т.е. дисперсии случ. переменных
одинаковы во все моменты измерения:
D{
}
=
,
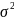t=1,…,T.
- гомоскедастичность
П4. Экз.переменные измеряются без ошибок. В случае модели множ.линейной регрессии их значения образуют линейно-независимые векторы.
П5. Закон распределения вероятностей случайной переменной принадлежит к классу нормальных распределений с нулевым мат.ожиданием и дисперсией , которая чаще всего неизвестна.
Чтобы применять регресс.анализ, необх. иметь сведения о корреляц.анализе.
Коррел.связь – связь, когда признак У реагирует на изменение другого признака х изменением своего частотного распределения.
Регресс.зависимость – зависимость условной средней арифметической выходного признака от изменений входного признака.
Парный коэффициент корреляции (r) – мера коррел. зависимости двух признаков. Принимает значения от -1 до 1; при преобразованиях сдвига и масштаба может только изменить знак без изменения значения; если r = 1 или -1, то существует линейная зависимость между х и У; если r =0, то делают вывод об отсутствии коррел.зависимости признаков.
=
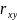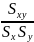- парный коэффициент корреляции Пирсона,
-
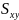ковариация между признаками,
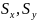- среднеквадратич.отклонения х и у.
3.Стат.Оценивание парам плр по мнк. Св-ва оценок.
Метод наименьших квадратов минимизирует сумму квадратов отклонений реальных наблюдений за эндогенной переменной от её значения, рассчитанного по модели. Является методом решения задачи: оценить неизвестные параметры регресс.модели, проверить гипотезы об их значимости и адекватности модели анализируемому эк.объекту.
МНК позволяет находить оценки, обеспеч.макс.точность (мин.дисперсию) в классе несмещённых и линейно связанных с наблюдениями y оценками.
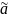мнк
= arg min
,
-
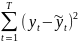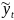оценённое (подстановочное) значение
энд.пер-ной от включения оценок неизвестных
параметров
=
+
+…+
.
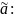
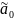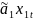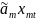Тогда
критерием качества оценивания явл.
сумма квадратов реально зарегистрированных
и подстановочных значений:
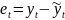- остаток (отклонение)модели.
МНК-оценки:
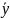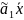мнк
=
-
, 
мнк
=
,
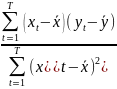где
=
,
=
.
=
+
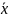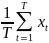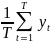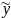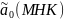(МНК)*х.
Оптимальность оценок МНК означает наличие свойств:
1)
оценки а0 и а1 имеют нормальные вероятностные
законы распределения и обладают свойством
несмещённости, т.е. мат.ожидание оценки
= соотв. характеристике генеральной
совокупности (искомому параметру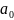): M{
}
=
,
M{
}
=
.
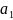Если
св-во нарушается, возникает смещённость
b=M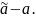
M{
(МНК)}=
+
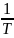ΣM{
}=
;
Дисперсия
этой оценки: D{
(МНК)}
= D{
}
+
=
=
=
.
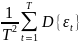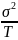Но т.к. она неизвестна=>
Дисперсию
заменяют несмещённой оценкой:
=
=
.
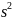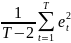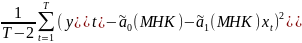2)предел
оценки с ростом выборки n
равен истинному значению параметра:
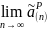= a,
P
= (|
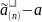|<ε)→1.
3)
если
несмещённая,
причём D
=minD
,
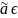A,
т.е. обладает равномерно-минимальной
дисперсией, то
- эффективная (оптимальная).
Фундаментальное свойство МНК: МНК-оценки параметров линейной регрессии обладают наименьшими дисперсиями среди множества всех несмещённых и линейно-зависимых от энд.перемен оценок в рамках модельных предположений 1-4. (Th Гаусса-Маркова)
Кроме точечных оценок использ. интервальные.
Доверительный интервал для :
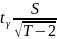(МНК)
-
<
<
(МНК)
+
,
γ
= 1-α,
α
– уровень значимости,
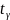= St(T-2),
- квантиль по табл Стьюдента.
Доверительный интервал для :
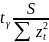(МНК)
-
<
<
(МНК)
+
,
где
=
-
.
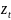
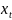