Теорема Ляпунова об асимптотической устойчивости по линейному приближению.
Теорема:
Рассмотрим систему
(1). Пусть A
– постоянная
матрица с действительными
коэффициентами, размера
.
А
– n-мерная
действительная вектор-функция,
непрерывная по y
в полуцилиндре:
,
причем
– не зависит
от x,
где
при
.
Далее, пусть
,
где
– собственное
значение матрицы A
(некоторые
могут совпадать),
.
Тогда нулевое
решение системы (1) асимптотически
устойчиво.
Доказательство:
◄ Мы сведем эту теорему к проверке выполнимости условия леммы Ляпунова об асимптотической устойчивости.
По лемме: существует матрица T с условием : матрица будет иметь вид:
,
где – собственное значение матрицы A (некоторые могут совпадать), а
(a – из условия теоремы). Положим , подставим в (1):
(2).
Положим:
,
.
Выполняется
условие леммы Ляпунова об асимптотической
устойчивости:
1)
– верно,
2)
,
,
Осталось проверить условие:
3)
.
Заметим, что
1)
,
2)
,
.
Проверку условия 3) проведем в 3 этапа.
Сделаем некоторые оценки.
Пусть
,
,
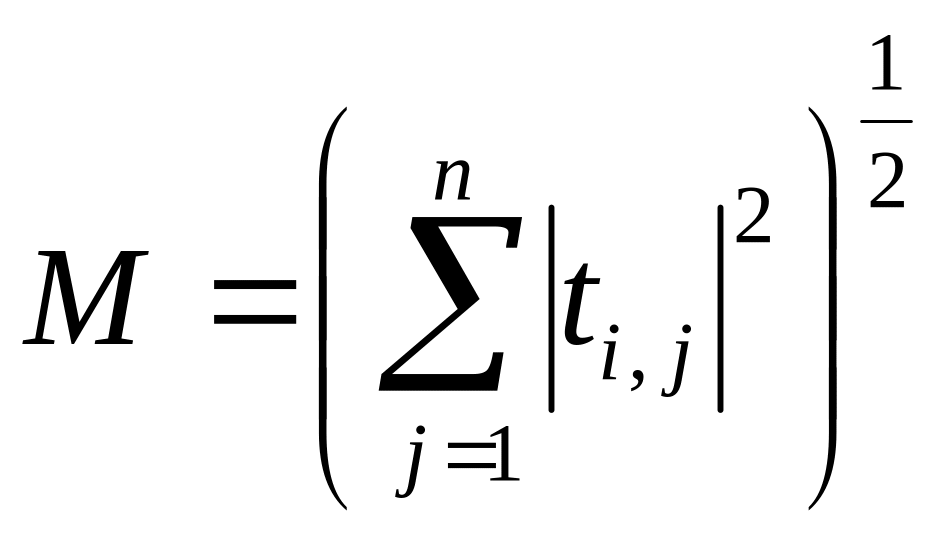тогда
Аналогично
.
(3)
Запишем подробно систему (2):
Пусть
– решение
системы (1), а
– решение
системы (2), тогда
Оценим каждое
.
.
.
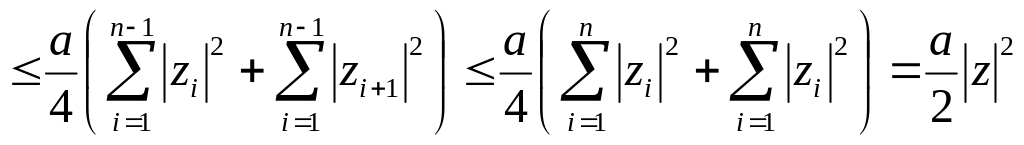при достаточно малых
,
так как
при
(то есть
,
).
Возьмем произвольную точку
из полуцилиндра
,
поскольку
через эту точку проходят интегральная
линия
(по теореме о
решения задачи
Коши), то в этой точке
будет
+
=
,
.
То есть выполняется условие леммы Ляпунова об асимптотической устойчивости. Следовательно нулевое решение системы (1) асимптотически устойчиво. ►
Лемма Адамара.
Лемма:
Пусть
– выпуклая
область в
(то есть
отрезок,
соединяющий
и
).
– метрическое
пространство, а функции
и
,
непрерывны
на
.
Тогда
,
,
где
непрерывна
на
,
.
Доказательство:
◄ По формуле Ньютона-Лейбница
=
=
=
.
Непрерывность
вытекает из
непрерывность интеграла по параметру
(по теореме из математического
анализа). ►
Замечание 1:
(надо подставить
вместо
)
Замечание 2:
Если
имеет непрерывные
смешанные производные по
до порядка
включительно
и эти производные непрерывны на
,
имеет непрерывную
смешанную производную по
и
(
)
до порядка
включительно
и эти производные непрерывны на
.
Это следует
из свойств интеграла (по теореме
из математического анализа).
Дифференцируемости решения системы оду по начальным данным и параметру.
Теорема:
Пусть
– область в
.
– отрезок, а
отображение
непрерывно,
,
и
так же непрерывны
на
,
.
Далее пусть
– решение
задачи Коши:
,
определенное на
.
Функции
,
,
,
при некотором
.
Причем
,
,
.
Теперь
Существует
единственное решение задачи Коши:
,
определенное так же на
,
причем
,
дифференцируема
по
при
и
,
удовлетворяет
условию
(5).
(6)
Замечание: Формулы (5) и (6) получаются формальным дифференцированием по , подстановкой и дифференцированием по тождества
Доказательство:
◄ По теореме о
непрерывном решении по начальным данным
и параметру существует
единственное решение
задачи (3), (4),
определенное на
,
при достаточно
малых
(то есть при
).
Далее
,
где
непрерывна
при
.
Положим
,
тогда
является
решением задачи Коши
,
функция
,
Далее
.
По теореме о
непрерывности по начальным данным и
параметру
,
где
– решение
задачи
и
– удовлетворяет
условиям (5), (6).
Теорема доказана. ►
Замечание:
Все сказанное
справедливо при
близких к
нулю, а не только при
,
то есть
удовлетворяет
уравнению
.
Это уравнение называется уравнением в вариациях.
Следствие 1:
Пусть в
предыдущей теореме
и
,
тогда
удовлетворяет
условиям
Следствие 2:
Пусть в
предыдущей теореме
и
,
тогда
удовлетворяет
условиям
− матрица Якоби
и удовлетворяет условиям
то есть
– резольвента
линейной системы
.
Следствие 3:
Пусть в
предыдущей теореме
и
,
тогда
удовлетворяет
условиям
