Резольвента линейной системы оду и ее свойства.

def: Резольвентой системы (2) называют отображение – множество невырожденных матриц порядка n, удовлетворяющих следующим условиям:

1) – ФМР системы (2),

2) .

Свойства:

1° – следует из определения.

2° Пусть – решение системы (2) с начальными условием , тогда .

Доказательство:

◄ Имеем

– решение системы (2),

причем . По теореме о единственности задачи Коши на . ►

3° (полугрупповое свойство)

Доказательство:

◄ Пусть – произвольный вектор из , тогда – значение в точке того решения системы (2), которое в точке равно (свойство 2°). – значения точки x того решения, которое в равно (свойство 2°), то есть того решения (в силу существования единственности), которое в точке равно . – значение в точке x того решения, которое в точке равно , в силу произвольного получаем требуемое. ►

4° . Это следует из 3°, так как (свойство 3°). Слева аналогично.

5°

Доказательство:

◄ = = = ►

Построение линейной, однородной системы по известной фср. Формула Лиувилля.

Теорема:

Пусть – произвольные n-мерные векторы-функции класса , причем , тогда система вида (2), для которой являются ФСР.

Доказательство:

◄ Рассмотрим систему

, .

Это система вида (2) (надо разложить по первому столбцу)

,

где – известные непрерывные функции на . Заметим, что – решение этой системы (так как при подстановке вместо y получаем два одинаковых столбца).►

Единственность.

Пусть – ФМР системы и . Тогда

.

Умножаем справа на ( – существует, так как ). Получим, что на .

Формула Лиувиля.

Пусть – ФСР системы (2), тогда , где

= = ,

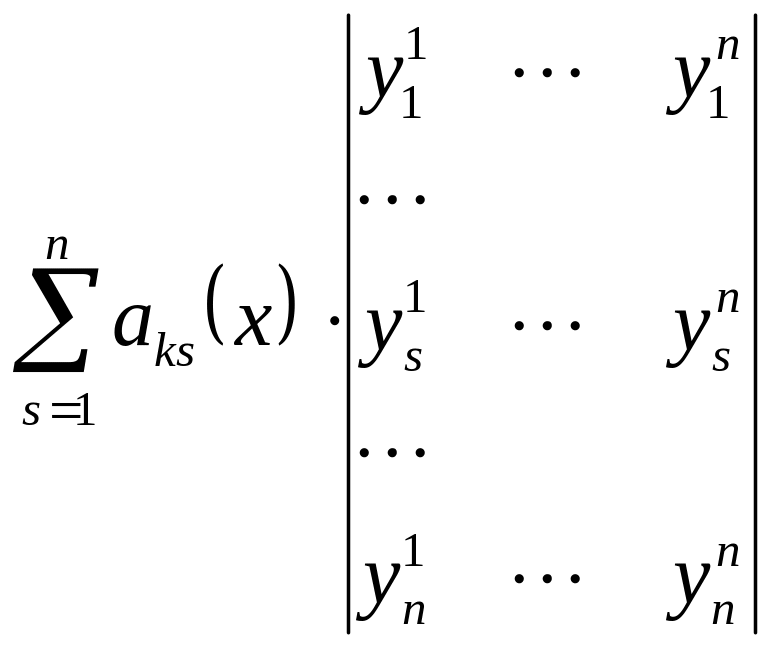так как при получаем две одинаковые строки

– Формула Лиувиля.

Нахождение частного решения линейной неоднородной системы ОДУ методом вариации постоянных. Формула Коши.

Рассмотрим систему:

(1)

(2) – собственная однородная система.

Будем искать частное решение системы (1) в виде:

(3)

,

где – ФСР собственной однородной системы (2), а – функции класса . Подставим y из (3) в (1):

( – существует, так как , )

= .

Итак, решение задачи Коши имеет вид:

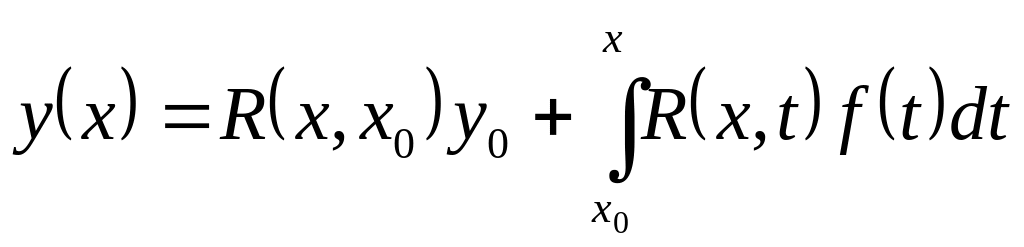
Линейные системы с постоянными коэффициентами и методы их решения Случай нормализуемой системы.

(1),

где , – многочлен от p с постоянными коэффициентами из C. Положим , – порядок системы (формальный).

,

– алгебраическое дополнение элемента в матрице . – (дифференциальный оператор, а не число). “Умножим” i-ое уравнение из (1) на слева и просуммируем по i, от 1 до n. (Если умножать элементы столбца матрицы на соответствующие алгебраические дополнения элементов того же столбца, то получим определитель матрицы, а если умножать на алгебраические дополнения другого столбца, то получим 0, на этом принципе построена обратная матрица.)

В итоге получим: (2) , . (В дальнейшем будет обосновано, что такое “умножение” возможно при достаточно гладких ).

Система (2) распадается на n независимых ОДУ, отличающихся только правыми частями. Заметим, что каждое (достаточно гладкое) решение системы (1) (или (1одн.)) является решением системы (2) (или (2одн.)), но не наоборот. Из прошлого семестра заключаем, что общее решение системы (2одн.) имеет вид: (3), где – корни характеристического уравнения , кратности , а – векторный многочлен, каждая компонента которого является многочленом степени . Для нахождения общего решения системы (1одн.) можно было бы подставить из (3) в (1одн.), найти соотношение между коэффициентами многочленов , выразить базисные неизвестные через свободные и обозначить эти свободные через . Однако это слишком сложно. Для упрощения докажем лемму.

Лемма:

Пусть – решение системы (1одн.) (как показано выше, охватывается формулой (3)). Тогда каждое слагаемое в записи (3) также является решением системы (1одн.) (то есть можно привести предыдущие рассмотрения для каждой в отдельности, что значительно проще).

Доказательство:

◄ Подставим в (1одн.): . Поскольку все функции линейно независимы при различных k и различных (“ФСР в случае кратных корней” – из прошлого семестра), то все коэффициенты всех многочленов в этом соотношении равны нулю. То есть

– решение системы (1одн.). ►

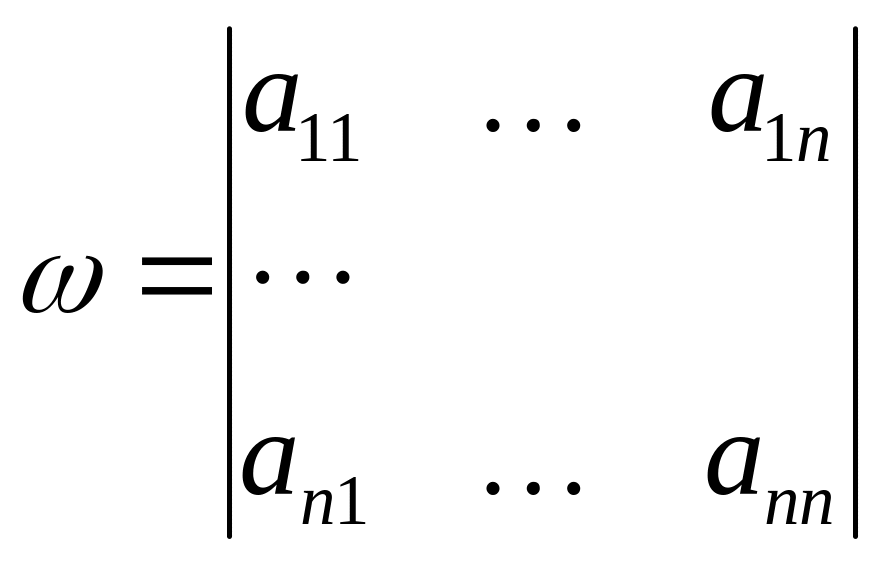
Таким образом, общая схема решения системы (1одн.) изложена. Осталось ее обосновать. Для этого положим: + младшие степени p, некоторые могут равняться нулю.

,

.

Рассмотрим два случая:

I случай: (случай нормализуемой системы).

, тогда система (1) примет вид:

Поскольку , то эту систему можно разрешить относительно , то есть .

Эта система каноническая и, следовательно, может быть сведена к нормальной (отсюда название “нормализуемая” система). ( – замечание о гладкости решения из прошлого семестра). Так же как и в прошлом семестре в этой системе можно показать, что если , то , в частности, если , то .