Устойчивость решения по Ляпунову и асимптотическая устойчивость. Лемма Ляпунова об устойчивости.

Рассмотрим систему:

(1).

Будем предполагать, что

1) решение системы (1) на участке , при условии ;

2) , , решение на участке , удовлетворяющее начальному условию .

def: Решение системы (1) называется устойчивым по Ляпунову, если , , , . Другими словами, устойчивость по Ляпунову – это непрерывная зависимость решения от изначально данного , равномерная на луче .

def: Решение системы (1) называется асимптотически устойчивым, если:

1) Оно устойчиво по Ляпунову;

2) , : при .

Пример 1:

– маятник без трения. Нулевое решение устойчиво, но не асимптотически устойчиво: .

Пример 2:

– маятник с трением.

Это затухающие колебания, нулевое решение асимптотически устойчиво.

Замечание: Исследовать устойчивость (асимптотическую) решения системы можно свести к исследованию устойчивости (асимптотической) нулевого решения некоторой другой системы.

Положим: ,

тогда . В дальнейшем будем исследовать устойчивость (асимптотическую) только нулевого решения.

Лемма Ляпунова об устойчивости.

Пусть функция – непрерывна по x и локально удовлетворяет условию Липшица по y, . Далее пусть удовлетворяет следующим условиям:

1) ;

2) ;

3)

Тогда нулевое решение системы (1) устойчиво по Ляпунову.

Доказательство:

◄ Фиксируем тогда в силу 2). Поскольку непрерывна в точке 0 и , то .Покажем, что это искомое, то есть , где – решение системы (1) с начальным условием . Допустим, что это не так, то есть . Положим , тогда в силу 3). То есть не возрастает (по теореме Лагранжа). С другой стороны – противоречие ►

Замечание: Функция называется функцией Ляпунова для системы (1)

Лемма Ляпунова об асимптотической устойчивости и ее усиленный вариант.

Пусть выполнены условия леммы Ляпунова об устойчивости. Далее пусть

удовлетворяет следующим условиям:

1) ;

2) ;

3) .

Тогда нулевое решение асимптотически устойчиво.

Доказательство:

◄ Сначала докажем усиленный вариант леммы Ляпунова об асимптотической устойчивости.

Усиленный вариант.

Пусть выполняется условие леммы Ляпунова об устойчивости. Далее пусть существует семейство непрерывных функций удовлетворяет следующим условиям:

1)

2) , .

Тогда нулевое решение системы (1) асимптотически устойчиво.

Доказательство:

◄ Фиксируем , , тогда (как и в доказательстве предыдущей леммы).

Пусть и . Покажем, что , при , где – решение системы (1) с начальным условием .

Как было показано в доказательстве предыдущей леммы функция не возрастает, заметим, что , так как . По теореме из анализа . Покажем, что . Допустим тогда в силу непрерывности функции и условия . В этом случае (если бы для некоторого ,то , а у нас , то есть ). (условие 2) для семейства ).

Так как Формула Ньютона-Лейбница.

(условие 1)) , при , а у нас и противоречие . То есть , при . Покажем, что , при . Допустим, что это не так, тогда , в этом случае . А у нас доказано, что при . Усиленный вариант доказан. ►

Перейдем к доказательству леммы Ляпунова об асимптотической устойчивости (в качестве следствия).

Достаточно положить . Очевидно, что:

1)

2) Если то .

, а тогда можно применить усиленный вариант. ►

Лемма по приведению матрицы к жордановой форме с ε вместо 1 под диагональю.

Пусть B – матрица, имеющая жорданову форму, то есть:

Тогда существует матрица такая, что

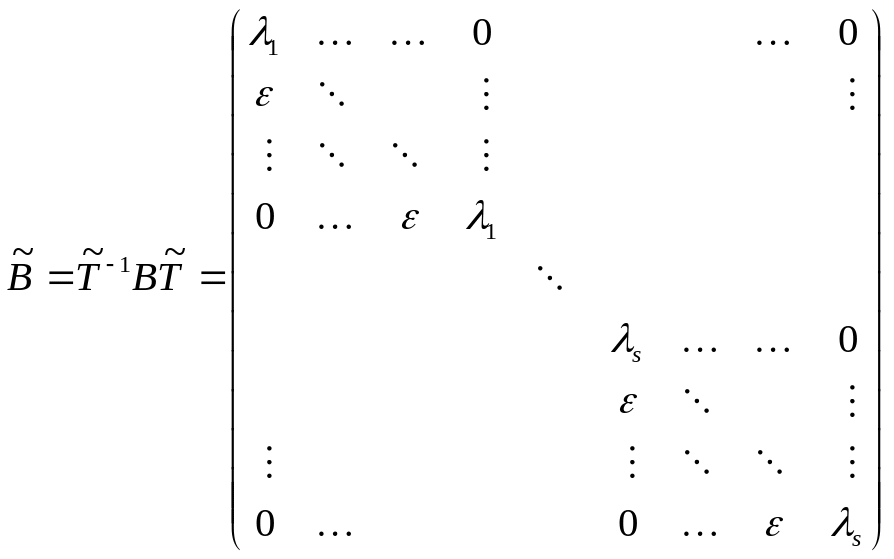
Докажем это для одной клетки.

Доказательство:

◄ Известно, что замена переменной переводит систему в систему . Построим для одной клетки:

Положим

.

Подставим это в систему :

Лемма доказана. ►