
- •2 Семестр.
- •Лектор: Сухинин м. Ф.
- •Канонические и нормальные системы оду. Порядок системы. Сведение системы к одному уравнению и наоборот.
- •Лемма Арцелы (критерий компактности).
- •Ломаные Эйлера и теорема Пеано.
- •Теорема о единственности решения задачи Коши для систем оду. Следствие для оду n-го порядка. Случай линейного уравнения и линейной системы.
- •Лемма о равномерной непрерывности.
- •Непрерывность решения системы оду по начальным данным и параметру.
- •2) , , : & Это следует из открытости множества, непрерывности в точке и условия . Выберем , .
- •Линейная зависимость и независимость вектор-функций. Определитель Вронского.
- •Фундаментальная система решений (фср) для линейной однородной системы оду. Существование фср и их взаимосвязь. Общее решение линейной однородной неоднородной системы.
- •Резольвента линейной системы оду и ее свойства.
- •Построение линейной, однородной системы по известной фср. Формула Лиувилля.
- •Линейные системы с постоянными коэффициентами и методы их решения Случай не нормализуемой системы.
- •Нормальные линейные системы с постоянными коэффициентами и методы их решения
- •Устойчивость решения по Ляпунову и асимптотическая устойчивость. Лемма Ляпунова об устойчивости.
- •Лемма Ляпунова об асимптотической устойчивости и ее усиленный вариант.
- •Теорема Ляпунова об асимптотической устойчивости по линейному приближению.
- •Лемма Адамара.
- •Дифференцируемости решения системы оду по начальным данным и параметру.
- •Первые интегралы систем дифференциальных уравнений. Задание общего решения системы с помощью полной системы первых интегралов.
- •Существование полной системы первых интегралов
- •Линейные однородные УрЧп первого порядка. Связь с первыми интегралами соответствующей системы оду. Замечание о квазилинейных уравнениях.
- •Квазилинейные УрЧп первого порядка. Две леммы о характеристиках.
- •Теорема о существовании единственного решения задачи Коши для квазилинейных УрЧп первого порядка в случае пространственных переменных.
- •По условию 4),
- •Оператор Штурма-Лиувилля. Его собственные функции. Лемма о нулевом собственном значении.
- •Представление решения краевой задачи для уравнения Штурма-Лиувилля через функцию Грина. Выражение функции Грина и ее свойства.
Лемма о равномерной непрерывности.
def: Метрическое пространство называется компактом, если из каждого покрытия его открытыми множествами (открытое покрытие) можно выделить конечное подпокрытие.
Лемма:
Пусть
![]() – метрические
пространства,
– метрические
пространства,
![]() – метрический
компакт, а
– метрический
компакт, а
![]() – непрерывно
на всем
– непрерывно
на всем
![]() ,
тогда
,
тогда
![]() – непрерывно
по
и эта
непрерывность равномерна
по
– непрерывно
по
и эта
непрерывность равномерна
по
![]() ,
то есть
,
то есть
![]() и
и
![]() ,
что
,
что
![]()
![]() ,
,
![]() выполняется
неравенство
выполняется
неравенство
![]() (то
есть
не зависит
от k).
(то
есть
не зависит
от k).
Доказательство:
◄ Выберем
произвольно
![]() и
.
Надо найти
.
В силу
непрерывности
и
.
Надо найти
.
В силу
непрерывности
![]() в точке
в точке
![]() имеем
имеем
![]()
![]()
![]()
![]()
![]()
![]() .
Используя
аксиому выбора можно считать, что задана
функция
.
Используя
аксиому выбора можно считать, что задана
функция
![]()
![]() на всем К.
Заметим:
на всем К.
Заметим:
![]() ,
где
,
где
![]()
![]() – открытый
шар в К,
с центром в
точке k,
радиуса
– открытый
шар в К,
с центром в
точке k,
радиуса
![]() .
В силу
компактности К,
имеем
.
В силу
компактности К,
имеем
![]() :
:
![]() .
Положим
.
Положим
![]() ,
тогда
,
покажем, что
это
– искомое.
,
тогда
,
покажем, что
это
– искомое.
Пусть
![]() ,
,
,
тогда
,
,
,
тогда
![]() ,
,
![]()
![]() ,
то есть
,
то есть
![]() .
Имеем:
.
Имеем:
![]() +
+![]() .
.
Так как:
![]() – для первого
слагаемого,
– для первого
слагаемого,
![]() – для второго
слагаемого. ►
– для второго
слагаемого. ►
Непрерывность решения системы оду по начальным данным и параметру.
Теорема:
Пусть
![]() – метрическое
пространство,
– метрическое
пространство,
![]() – открытое
множество в
– открытое
множество в
![]() ,
функция
,
функция
![]() – непрерывна
на
,
ограничена
– непрерывна
на
,
ограничена
![]() ,
удовлетворяет
условию Липшица по у.
Далее: пусть
– решение
задачи Коши:
,
удовлетворяет
условию Липшица по у.
Далее: пусть
– решение
задачи Коши:
![]() ,
при
,
при
![]() ,
,
![]() и
и
![]() ,
определенное
на
.
Тогда
,
определенное
на
.
Тогда
![]() ,
что
,
что
![]() =
=
![]() !
решение
!
решение
![]() задачи (1), (2),
определенное на всем
,
причем
– непрерывно
по
задачи (1), (2),
определенное на всем
,
причем
– непрерывно
по
![]() ,
и эта
непрерывность равномерна
по
,
то есть
,
и эта
непрерывность равномерна
по
,
то есть
![]() ,
,
,
,
![]() ,
,
![]()
![]()
Доказательство:
◄ 1)
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
Допустим, что это не так. Тогда
![]()
![]() ,
,
![]() ,
,
![]() ,
точка
,
точка
![]() ,
,
![]()
![]() .
.
По теореме Больцано-Вейерштрассе:
![]() .
Заметим,
что
.
Заметим,
что
![]()
![]()
![]() ,
,
так как
непрерывна
в точке
![]() .
В этом случае
.
В этом случае
![]() ,
так как
,
так как
![]() ,
определена
по условию на всем
,
то есть
,
определена
по условию на всем
,
то есть
![]() и точку
и точку
![]() можно считать
аргументом
(то есть можно
подставлять в уравнение
(1)).
можно считать
аргументом
(то есть можно
подставлять в уравнение
(1)).
Поскольку
![]() определено
на
,
то его можно
подставить в (1)
определено
на
,
то его можно
подставить в (1)
![]() – имеет смысл
– имеет смысл
![]() .
В силу открытости
D, точка
.
В силу открытости
D, точка
![]() ,
при достаточно
больших k,
а это противоречит
выбору точек
,
при достаточно
больших k,
а это противоречит
выбору точек
![]()
![]() .
.
2) , , : & Это следует из открытости множества, непрерывности в точке и условия . Выберем , .
Пусть
![]() ,
тогда точка
в силу 2) и
существует единственное
решение
задачи Коши
(1), (2), определенное в окрестности
точки h.
Заметим так
же, что
определена в
окрестности точки h
(поскольку
,
D –
открыто
и
– непрерывна
в точке h).
,
тогда точка
в силу 2) и
существует единственное
решение
задачи Коши
(1), (2), определенное в окрестности
точки h.
Заметим так
же, что
определена в
окрестности точки h
(поскольку
,
D –
открыто
и
– непрерывна
в точке h).
Сделаем оценки:
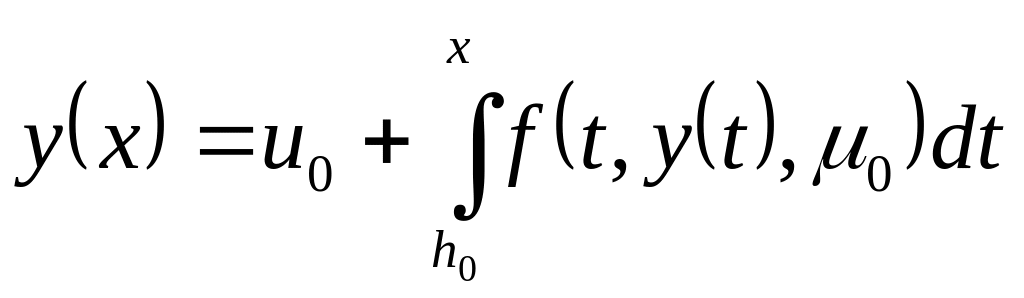 =
= +
+![]() ,
=
,
=
и вычитаем из одного другое:
![]()
![]() +
+
![]() +
+
+
+![]()
![]() +
+![]() +
+
+
+![]()
(заметим,
что
![]() определено
при всех
определено
при всех
![]() и
и
![]()
![]() );
непрерывна
по
);
непрерывна
по
![]() ,
,
![]() ;
по лемме о
равномерной непрерывности:
;
по лемме о
равномерной непрерывности:
![]() при
при
![]() равномерно
по
,
а тогда
равномерно
по
,
а тогда
![]() при
при
![]() )
)
![]()
![]()
(По замечанию к лемме Гронуолла)
![]()
![]()
![]()
(не зависит от x и при достаточно малых ).
Продолжим
вплоть до
границы трубки
![]()
В силу
график
продолженного решения
![]() выйдет
на границу
выйдет
на границу
![]() только при
и
.
только при
и
.
Из первой части
следует, что
![]() непрерывно
по
непрерывно
по
![]() в точке
в точке
![]() ,
равномерно
по
,
равномерно
по
![]() .
Проводя для
те же рассуждения,
что и для
,
получим, что
непрерывно
по
,
равномерно
по
в окрестности
точки
,
а не только в
самой точке
.
►
.
Проводя для
те же рассуждения,
что и для
,
получим, что
непрерывно
по
,
равномерно
по
в окрестности
точки
,
а не только в
самой точке
.
►
