По условию 4),

где , , (можно считать, что настолько мало, что это выполняется ) в силу следствия 1 из теоремы о дифференцируемости по начальным данным и параметру

то теореме об обратной функции (можно считать, что при ( ), то есть можно выбрать достаточно малым).

− открытая окрестность точки на плоскости и − диффеоморфизм класса , так как инъективно и также .

4) Поскольку − компакт в и , а открыто в , то

Положим

Очевидно, что .

5. Докажем, что , , инъективно.

Допустим, что это не так. Тогда , , . По теореме Больцано-Вейерштрассе и , Так как непрерывна, то . По условию 3 теоремы (обозначение). Поскольку при некотором , открыто в и взаимно-однозначно, то при достаточно больших , а это противоречит выбору и Противоречие! Итак : − диффеоморфизм класса и − открытая окрестность .

6) Построим решение УрЧП (1) следующим образом: пусть . Положим и (см. 2)). Тогда , так как по и , а по построению, . Итак, .

По второй лемме о характеристиках − решение УрЧП (1), причем с поверхности .

7) Единственность. Путь − так же решение УрЧП (1) в и с поверхности . Пусть . Положим и допустим, что . Проведем через характеристику . По первой лемме о характеристиках

(Если , и , то может так как зависит от продолжения на , а это продолжение не единственно) ►

Оператор Штурма-Лиувилля. Его собственные функции. Лемма о нулевом собственном значении.

, , (1)

(2)

Область определения оператора Штурма-Лиувилля:

это оператор Штурма-Лиувилля.

def: Функция называется собственной функцией оператора Штурма-Лиувилля, отвечающей собственному значению , если

1)

2)

3) .

Лемма о нулевом собственном значении оператора Штурма-Лиувилля.

Лемма:

Число является собственным значением оператора Штурма-Лиувилля . При этом является собственной функцией оператора Штурма-Лиувилля, отвечающей собственному значению .

Доказательство:

◄ ( ) Пусть − собственное значение и − соответствующая собственная функция. Тогда

Так как , то

.

(Если , например , то , так как )

Аналогично

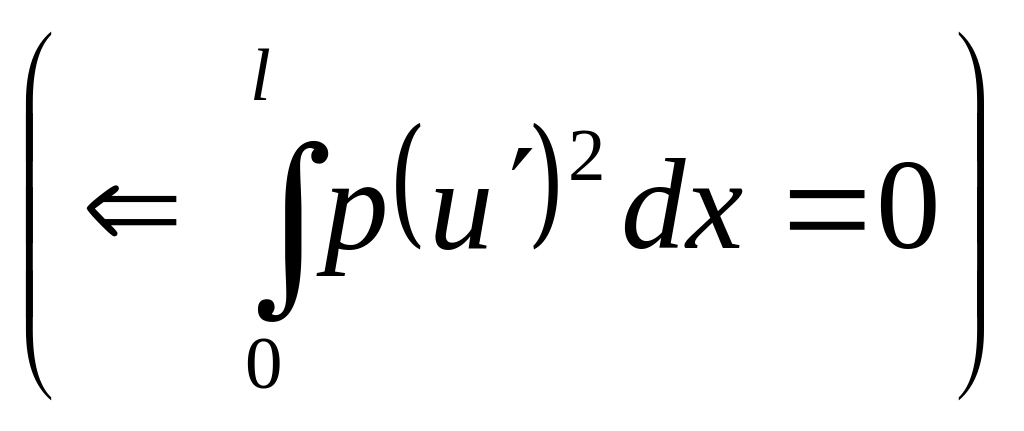
( ) Пусть , , . Положим , тогда , , так как и ►

Представление решения краевой задачи для уравнения Штурма-Лиувилля через функцию Грина. Выражение функции Грина и ее свойства.

Пусть не является собственным значением оператора Штурма-Лиувилля. Тогда функцией Грина называется:

,

где удовлетворяет однородному уравнению (1одн.) .

(то есть удовлетворяет левому граничному условию),

(то есть удовлетворяет правому граничному условию),

– определитель Вронского.

Свойства функции Грина.

1) вещественна и непрерывна на ,

в замкнутых треугольниках

и

2) (симметричность)

3) (удовлетворяет однородному уравнению (1одн.))

4) , (условие скачка производно по диагонали)

5) (удовлетворяет краевым условиям (2))

При этом решение краевой задачи (1), (2) равно

.