
- •II семестр
- •Элементарные преобразования матрицы
- •Ранг матрицы
- •Системы линейных алгебраических уравнений
- •Линейные пространства.
- •Линейная зависимость и линейная независимость векторов линейных пространств.
- •Подпространство линейного пространства
- •Ядро, образ, ранг, дефект.
- •Операторы простой структуры
- •Координаты вектора в ортонормированном базисе
- •Матрица Грама
- •Ортогональное дополнение к подпространству
- •Ортогональные операторы
- •Самосопряжённые операторы
- •Квадратичная форма
- •Канонический вид квадратичной формы
- •Знакопостоянные квадратичные формы
- •Приведение общего уравнения кривой второго порядка к каноническому виду
Самосопряжённые операторы
Линейный оператор
B
называется сопряжённым к оператору
,
если
![]() для
.
Обозначение:
для
.
Обозначение:
![]() .
.
 .
.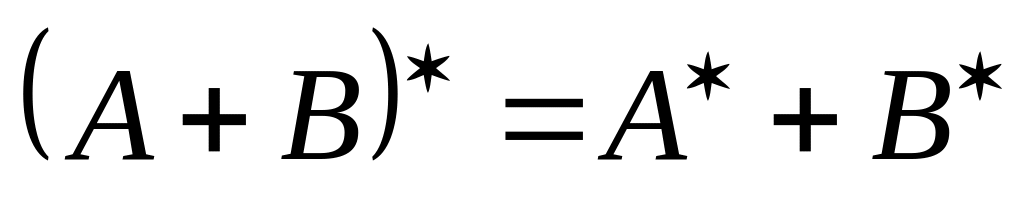 .
. .
. .
. .
.
Линейный оператор
называется самосопряжённым, если
![]() .
.
Теорема о
матрице сопряжённого оператора:
Если A
– матрица оператора C
в ортонормированном базисе, то
![]() – матрица оператора
– матрица оператора
![]() в том же базисе.
в том же базисе.
Пусть
– матрица оператора C
и
 – матрица оператора
в ортонормированном базисе
.
Из определения сопряжённого оператора
следует, что
– матрица оператора
в ортонормированном базисе
.
Из определения сопряжённого оператора
следует, что
![]() .
Тогда
.
Тогда
![]() и
и
![]() для
для
![]() .
.
Матрица самосопряжённого оператора в любом ортонормированном базисе симметричная.
Собственные векторы самосопряжённого оператора, отвечающие различным собственным числам ортогональны.
Пусть
![]() – собственные числа и
и
– отвечающие им собственные векторы
самосопряжённого оператора A.
Тогда
– собственные числа и
и
– отвечающие им собственные векторы
самосопряжённого оператора A.
Тогда
![]() .
При этом
.
При этом
![]() ,
а
,
а
![]()
![]() .
.
Если A – самосопряжённый оператор, то в существует ортонормированный базис из собственных векторов оператора A.
Квадратичные формы
Линейные формы
Говорят, что в
задана линейная форма (линейный
функционал)
![]() ,
если каждому
,
если каждому
![]() из
поставлено в соответствие число
из
поставлено в соответствие число
![]() так, что выполняются два условия:
так, что выполняются два условия:
 для
для
 из
.
из
. для
для
 из
.
из
.
Если
– линейная форма в
,
то существуют числа
![]() ,
где
,
где
![]() – координаты
для
в фиксированном базисе.
– координаты
для
в фиксированном базисе.
Пусть в
выбран базис
.
Тогда
может быть представлен в виде
![]() и
и
![]() ,
где
,
где
![]() .
.
Если в
задан ортонормированный базис, то любую
линейную форму
модно представить в виде
![]() ,
где
,
где
![]() .
.
Билинейные формы
Говорят, что в
задана билинейная форма
![]() ,
если каждой паре векторов
и
поставлено в соответствие число
:
,
если каждой паре векторов
и
поставлено в соответствие число
:
– линейная форма, зависящая от при фиксированном .
– линейная форма, зависящая от при фиксированном .
Теорема о матрице билинейной формы:
Если в
задана билинейная форма
,
то существуют числа
,
где
![]() ,
где
,
где
![]() – координаты
– координаты
![]() – координаты
в фиксированном базисе.
– координаты
в фиксированном базисе.
Из условия теоремы следует, что
![]() ,
где
– фиксированный базис. Тогда
,
где
– фиксированный базис. Тогда
![]() .
.
Матрица
![]() называется матрицей билинейной формы.
называется матрицей билинейной формы.
Ранг матрицы билинейной формы называют рангом билинейной формы.
Билинейную форму
модно записать в виде
 ,
где
,
где
![]() .
.
Теорема о связи матриц билинейной
формы в разных базисах: Если
![]() –
матрица билинейной формы в базисе
–
матрица билинейной формы в базисе
![]() ,
а
,
а
![]() – матрица билинейной формы в базисе
,
то
– матрица билинейной формы в базисе
,
то
![]() ,
где C
– матрица перехода от базиса
к базису
.
,
где C
– матрица перехода от базиса
к базису
.
Пусть
![]() в базисе
в базисе
![]() в базисе
.
Тогда билинейная форма
в базисе
.
Тогда билинейная форма
![]()
 .
Кроме того,
.
Кроме того,
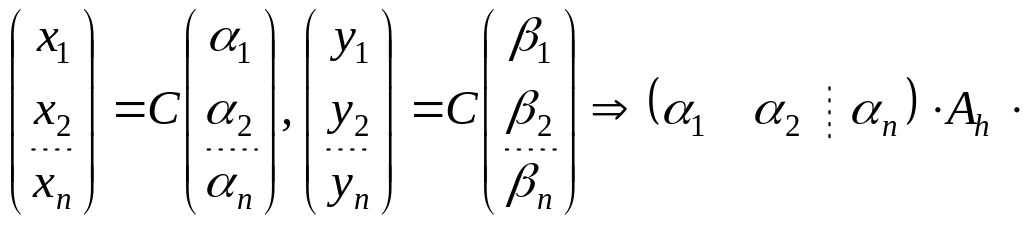
 .
.
Билинейная форма называется
симметричной, если
![]() .
.
Матрица симметричной
билинейной формы симметрична (т.к.
![]() ).
).
Квадратичная форма
Говорят, что в
задана квадратичная форма
![]() ,
если каждому
из
поставлено в соответствие число
,
если каждому
из
поставлено в соответствие число
![]() ,
где
,
где
![]() – симметричная билинейная форма.
– симметричная билинейная форма.
Симметричная билинейная форма, по которой построена квадратичная форма, называется полярной билинейной формой по отношению к квадратичной форме.
По заданной квадратичной форме можно восстановить полярную билинейную к ней форму.
Пусть
– квадратичная форма. Тогда
![]() ,
откуда
,
откуда
![]() .
.
Матрица билинейной формы, полярной по отношению к данной квадратичной форме, называется матрицей квадратичной формы.
Матрица квадратичной формы в любом базисе симметрична.
Пусть A – матрица квадратичной формы в базисе . Тогда
 и
и
 ,
где f
– билинейная форма, полярная данной
квадратичной.
,
где f
– билинейная форма, полярная данной
квадратичной.
Пусть – матрица квадратичной формы в базисе . Тогда
 ,
где C
– матрица перехода из базиса
в базис
.
,
где C
– матрица перехода из базиса
в базис
.
