
- •II семестр
- •Элементарные преобразования матрицы
- •Ранг матрицы
- •Системы линейных алгебраических уравнений
- •Линейные пространства.
- •Линейная зависимость и линейная независимость векторов линейных пространств.
- •Подпространство линейного пространства
- •Ядро, образ, ранг, дефект.
- •Операторы простой структуры
- •Координаты вектора в ортонормированном базисе
- •Матрица Грама
- •Ортогональное дополнение к подпространству
- •Ортогональные операторы
- •Самосопряжённые операторы
- •Квадратичная форма
- •Канонический вид квадратичной формы
- •Знакопостоянные квадратичные формы
- •Приведение общего уравнения кривой второго порядка к каноническому виду
Элементарные преобразования матрицы
Элементарными преобразованиями матрицы называются:
Перестановка двух строк (столбцов) матрицы местами.
Умножение строк (столбца) матрицы на произвольное число, не равное нулю.
Прибавление одной строки (столбца) матрицы к другой строке (столбцу).
Теорема Гаусса: Произвольную ненулевую матрицу с помощью элементарных преобразований можно привести к трапециевидной форме.
Рассмотрим матрицу
.
Если
![]() ,
то выбираем ненулевой элемент в первом
столбце. Если
,
то выбираем ненулевой элемент в первом
столбце. Если
![]() ,
то меняем местами первую и i-ю
строки. Если же все элементы первого
столбца нулевые, то ищем по первой
строке. Если
,
то меняем местами первую и i-ю
строки. Если же все элементы первого
столбца нулевые, то ищем по первой
строке. Если
![]() ,
то меняем местами первый и j-й
столбец. Если и первая строка нулевая,
то переставляем её в конец и повторяем
операцию для второго столбца. В результате
получится, что
,
то меняем местами первый и j-й
столбец. Если и первая строка нулевая,
то переставляем её в конец и повторяем
операцию для второго столбца. В результате
получится, что
![]() .
Теперь можно с помощью первой строки
обнулить первый столбец. Для этого к
строке 2 прибавим строку 1, умноженную
на
.
Теперь можно с помощью первой строки
обнулить первый столбец. Для этого к
строке 2 прибавим строку 1, умноженную
на
![]() ,
затем к строке 3 прибавим строку 1,
умноженную на
,
затем к строке 3 прибавим строку 1,
умноженную на
![]() и т.д. пока не получится
и т.д. пока не получится
 .
Повторим теперь всю операцию для матрицы
.
Повторим теперь всю операцию для матрицы
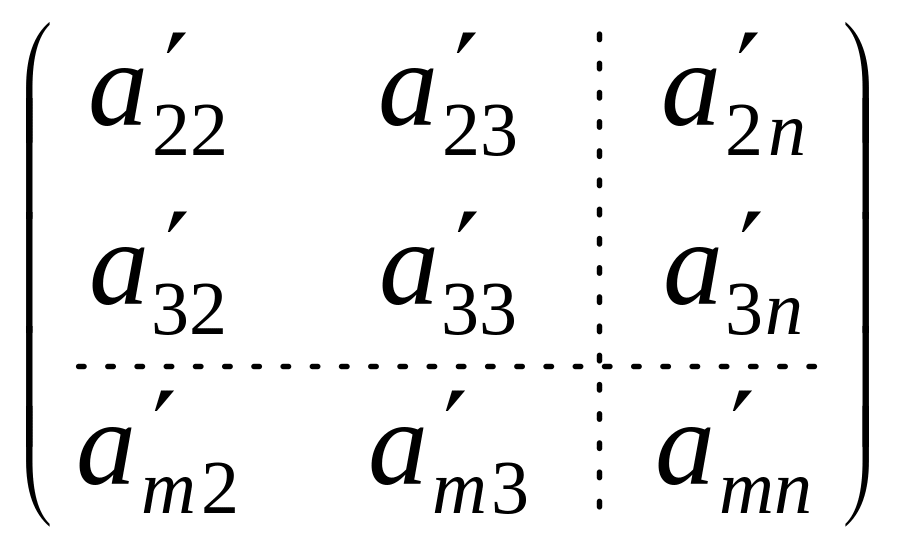 .
Продолжая весь этот цикл, получим
трапециевидную (треугольную) матрицу.
.
Продолжая весь этот цикл, получим
трапециевидную (треугольную) матрицу.
Если исходная матрица квадратная, то она будет приведена к верхней треугольной.
Определитель треугольной матрицы равен произведению её диагональных элементов.
Для доказательства достаточно разложить матрицу по первому столбцу. Получив произведение первого элемента на его алгебраическое дополнение, надо вновь разложить это дополнение по первому столбцу. В результате придём к произведению диагональных элементов.
Матрица B
называется обратной матрице A
, если
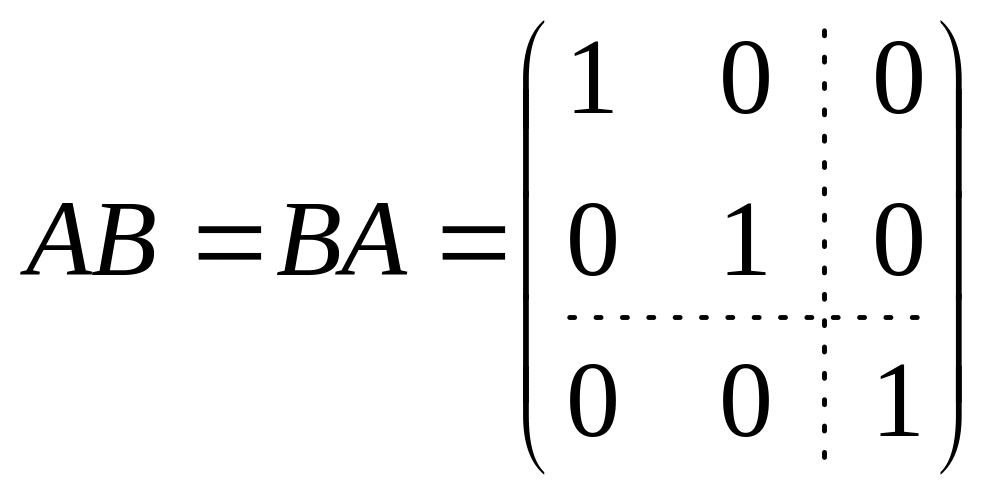 ..
..
Критерием существования обратной матрицы для матрицы A является её невырожденность (т.е. определитель матрицы не равен нулю).
Для доказательства достаточно построить
матрицу, обратную матрице
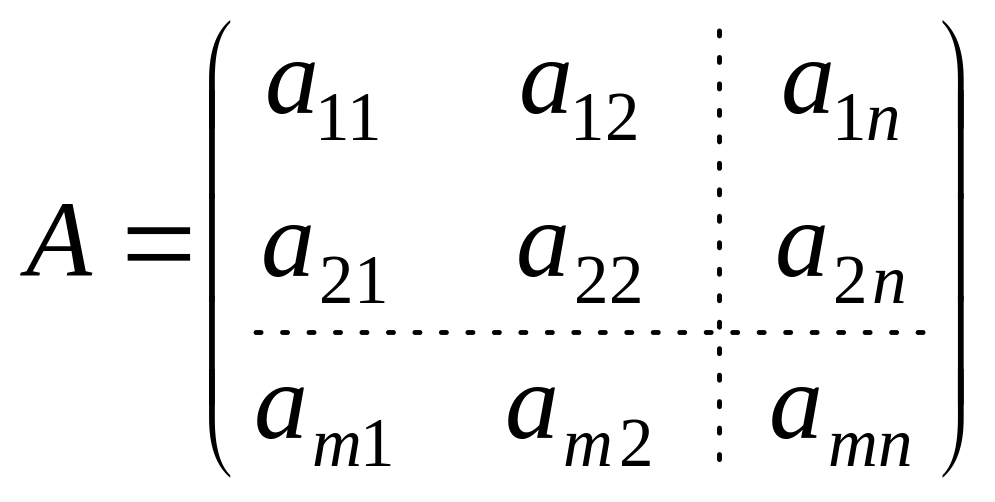 .
Для этого
.
Для этого
Транспонируем матрицу
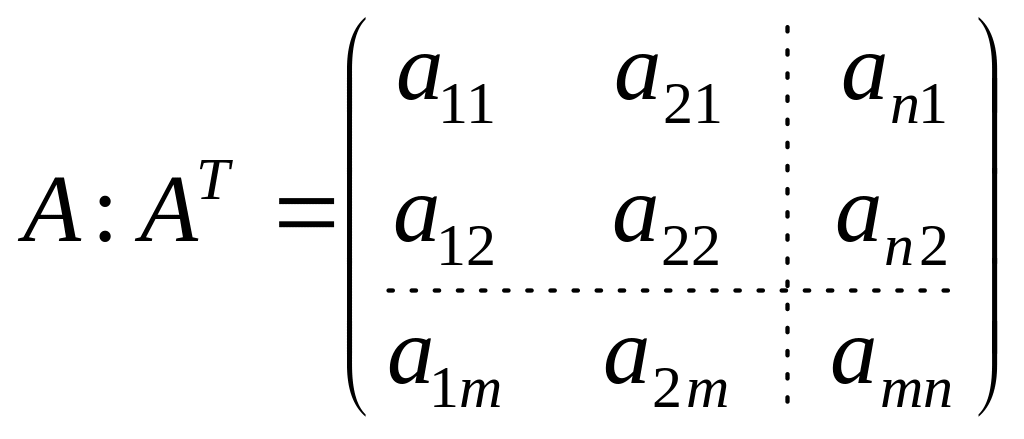 .
.Составим матрицу из алгебраических дополнений элементов матрицы
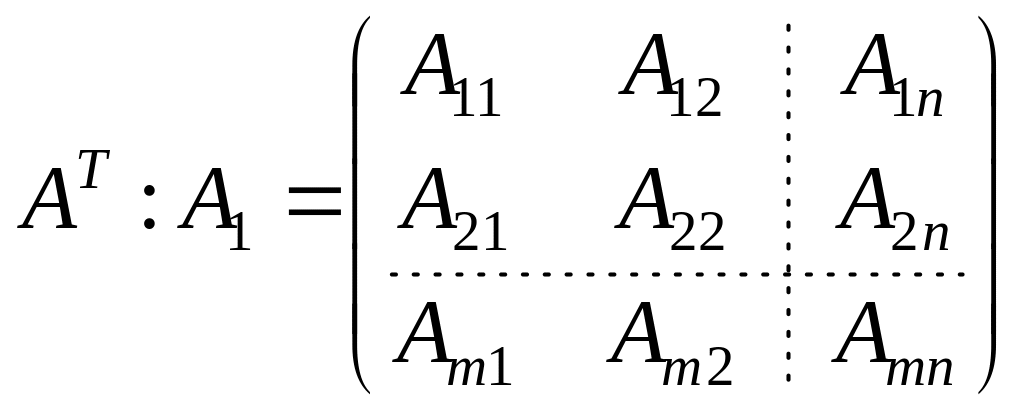 .
.Умножим
 на
на
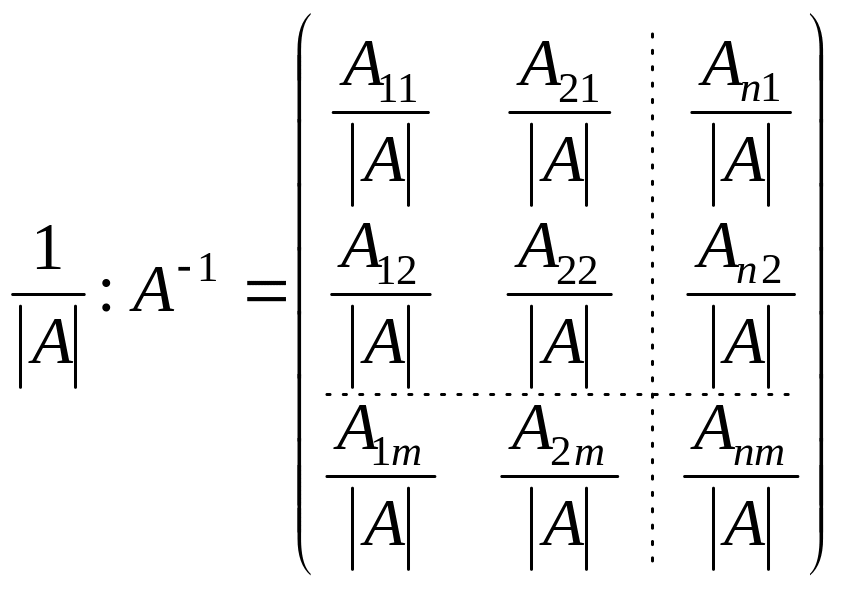 .
Матрица
.
Матрица
 - обратная матрице A.
- обратная матрице A.
Докажем необходимость: пусть для A
![]() .
Тогда
.
Тогда
![]() ,
т.е.
,
т.е.
![]() .
.
Ранг матрицы
Вектор-строки (столбцы) называют линейно зависимыми, если хотя бы одна из строк (столбцов) может быть выражена через другие.
Базисным минором произвольной матрицы называют отличный от нуля минор, при условии, что все миноры более высокого порядка равны нулю или не существуют.
Строки матрицы, на которых расположен базисный минор, называют базисными.
Теорема о базисном миноре: Базисные строки (столбцы) линейно независимы. Любая строка (столбец) матрицы может быть выражена через базисные.
Рангом матрицы называют порядок базисного минора.
Ранг ступенчатой (трапециевидной) матрицы равен числу ненулевых строк.
Элементарные преобразования не меняют ранг матрицы.
Зная ранг матрицы можно найти базисный минор, учитывая, что его порядок равен рангу матрицы.
Системы линейных алгебраических уравнений
Уравнение вида
![]() ,
где
,
где
![]() и b
– числа, а
и b
– числа, а
![]() – переменные, называется линейным
алгебраическим уравнением. Здесь
– коэффициенты уравнения, b
– свободный член.
– переменные, называется линейным
алгебраическим уравнением. Здесь
– коэффициенты уравнения, b
– свободный член.
Упорядоченный набор чисел
![]() называют решением этого уравнения, если
после подстановки
называют решением этого уравнения, если
после подстановки
![]() ,
уравнение превращается в верное
равенство.
,
уравнение превращается в верное
равенство.
Решить такое уравнение – значит найти все его решения или установить, что их нет.
Возможны три случая:
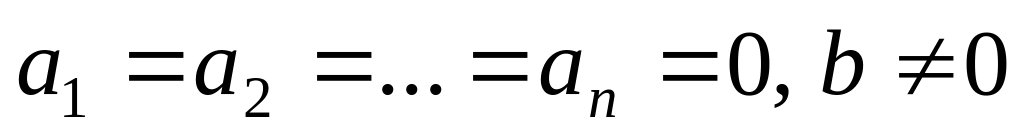 – нет решений.
– нет решений.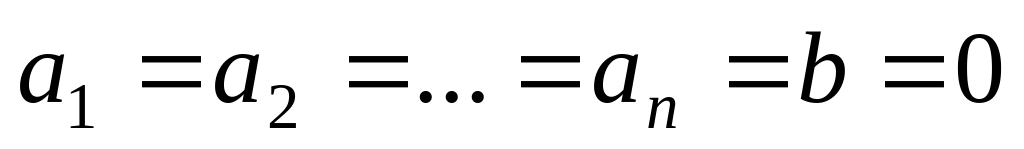 – решений бесконечно много.
– решений бесконечно много.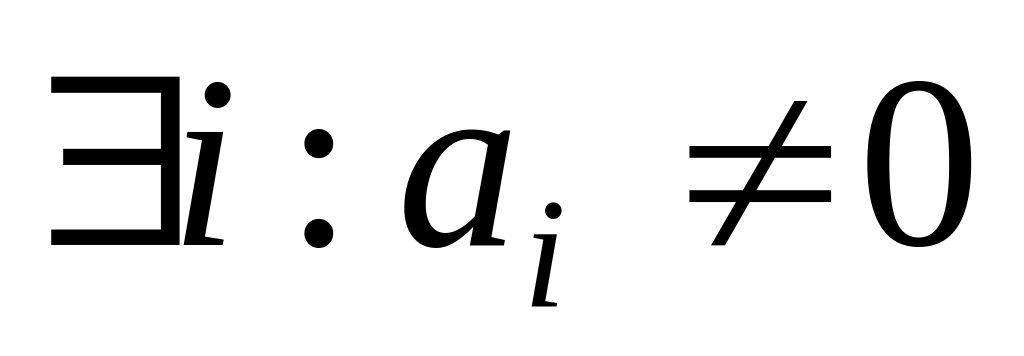 – решений бесконечно много.
– решений бесконечно много.
В последнем случае
![]() – общее решение для этого уравнения.
– общее решение для этого уравнения.
Система линейных алгебраических уравнений:
![]()
Решением системы линейных уравнений называется упорядоченный набор чисел, который удовлетворяет всем уравнениям системы.
Две системы называются равносильными, если совпадает множество решений.
Решить систему линейных уравнений значит:
Установить, имеет ли она решения.
Если имеет, выяснить, определённая она или нет (имеет ли конечное число решений).
Если определённая, то найти решения, иначе найти множество решений.
Система называется квадратной, если число неизвестных и решений совпадают.
Система линейных алгебраических уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Совместная система линейных алгебраических уравнений называется определённой, если она имеет только одно решение, и неопределённой, если она имеет более одного решения.
Квадратная система линейных уравнений с невырожденной матрицей называется крамеровской.
Теорема Крамера: Крамеровская система всегда совместна и определённа.
Пусть дана система
![]() ,
где
,
где
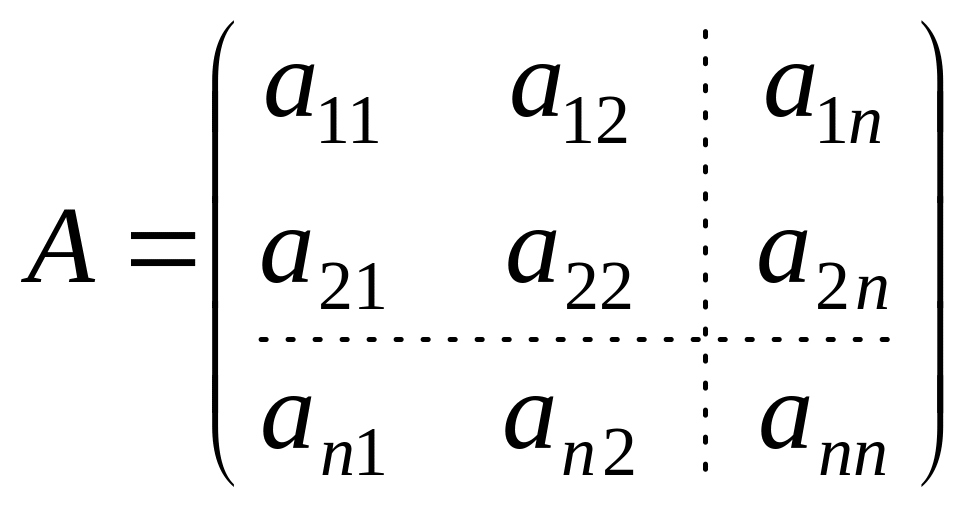 ,
,
![]() ,
,
![]() .
Покажем, что эта система имеет решение
.
Покажем, что эта система имеет решение
![]() .
Для этого подставим выражение для
.
Для этого подставим выражение для
![]() в уравнение системы. Получим
в уравнение системы. Получим
![]() ,
т.е.
,
т.е.
![]() .
Предположим, что
.
Предположим, что
![]() .
Тогда
.
Тогда
![]() ,
т.е.
,
т.е.
![]() ,
т.е. система имеет единственное решение.
,
т.е. система имеет единственное решение.
Пусть дана крамеровская система
![]() и пусть
– решения этой системы. Подставим их в
систему:
и пусть
– решения этой системы. Подставим их в
систему:
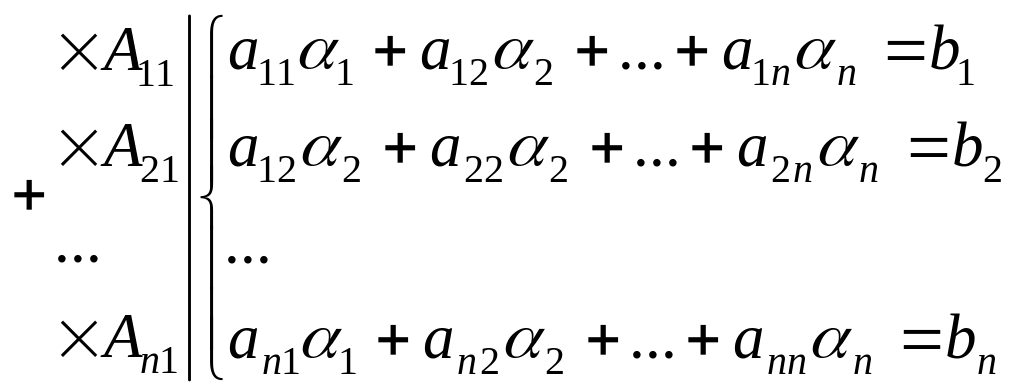 ,
где
,
где
![]() – алгебраическое дополнение элемента
– алгебраическое дополнение элемента
![]() в матрице системы. Получим:
в матрице системы. Получим:
![]()
![]() .
Обозначим определитель матрицы через
и определитель
матрицы, в которой i-й
столбец заменён столбцом свободных
членов, через
.
Обозначим определитель матрицы через
и определитель
матрицы, в которой i-й
столбец заменён столбцом свободных
членов, через
![]() .
Тогда в правой части равенства находится
.
Тогда в правой части равенства находится
![]() ,
а в левой –
,
а в левой –
![]() и, таким образом,
и, таким образом,
![]() .
Повторив эту операцию для всех столбцов
алгебраических дополнений, получим:
.
Повторив эту операцию для всех столбцов
алгебраических дополнений, получим:
![]() .
Эти формулы называются
формулами Крамера.
.
Эти формулы называются
формулами Крамера.
Теорема Кронекера-Капелли: Для того чтобы прямоугольная система линейных алгебраических уравнений (СЛАУ) была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы. При этом если ранг матрицы системы равен числу неизвестных, то система определённая, а если меньше, то неопределенная.
Обозначения:
- прямоугольная система.
![]() - расширенная матрица.
- расширенная матрица.
Пусть прямоугольная СЛАУ совместная и – решения системы. Выполним преобразования:
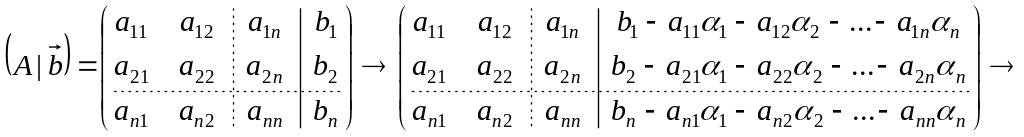
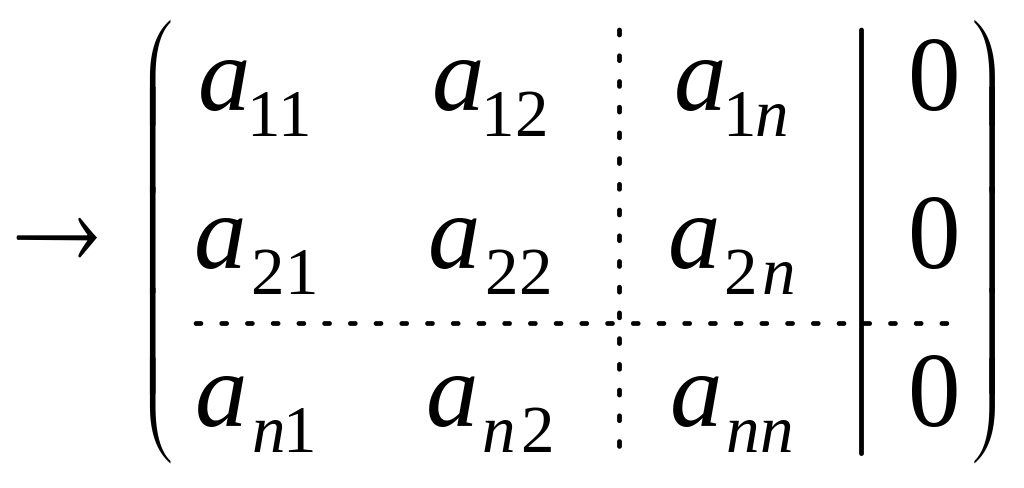 .
Т.к. это преобразование не влияет на
ранг матрицы и т.к. последний столбец
нулевой, то ранг этой матрицы равен
рангу матрицы системы, но, с другой
стороны, он равен рангу расширенной
матрицы системы.
.
Т.к. это преобразование не влияет на
ранг матрицы и т.к. последний столбец
нулевой, то ранг этой матрицы равен
рангу матрицы системы, но, с другой
стороны, он равен рангу расширенной
матрицы системы.Пусть
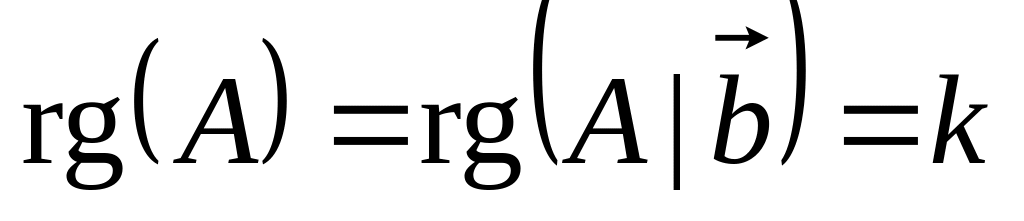 .
Тогда СЛАУ будет содержать k
линейно независимых уравнений и не
больше. При этом возможны два случая:
если
.
Тогда СЛАУ будет содержать k
линейно независимых уравнений и не
больше. При этом возможны два случая:
если
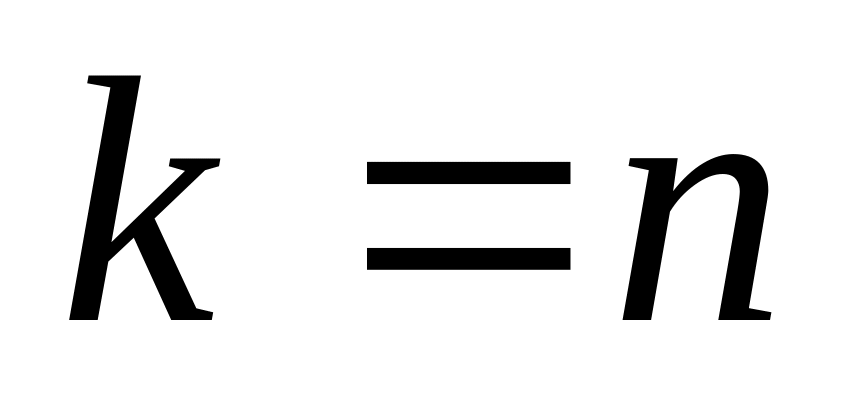 ,
то мы получаем крамеровскую систему k
уравнений с k
неизвестными. Если же
,
то мы получаем крамеровскую систему k
уравнений с k
неизвестными. Если же
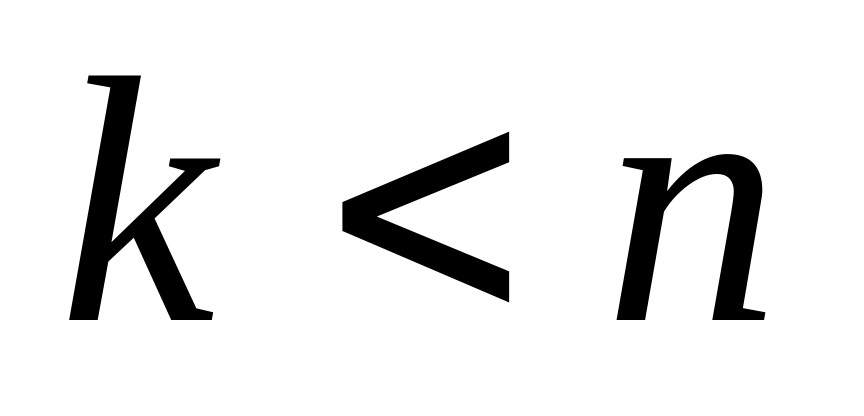 ,
то система содержит
,
то система содержит
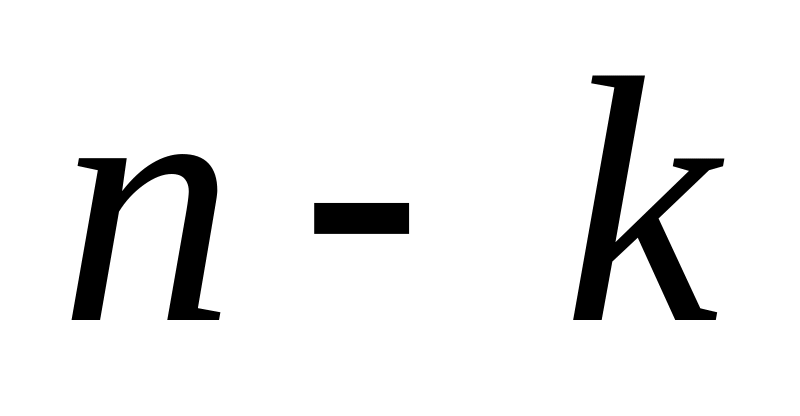 «лишних» неизвестных. Не умаляя общности,
будем считать, что базисными столбцами
являются первые k
столбцов матрицы системы. Неизвестные,
соответствующие базисным столбцам
будем называть базисными, а остальные
– свободными. Перепишем СЛАУ в виде
«лишних» неизвестных. Не умаляя общности,
будем считать, что базисными столбцами
являются первые k
столбцов матрицы системы. Неизвестные,
соответствующие базисным столбцам
будем называть базисными, а остальные
– свободными. Перепишем СЛАУ в виде
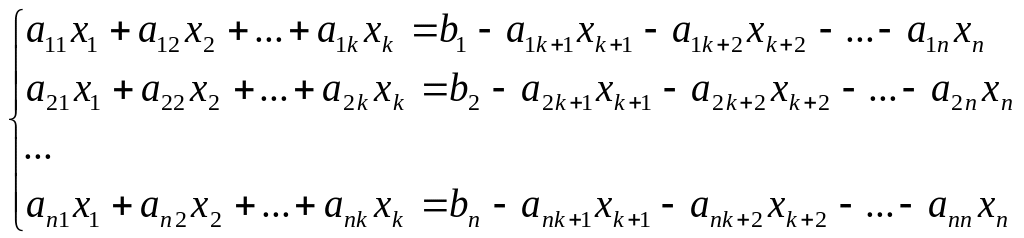 .
Полученная система является крамеровской
и имеет единственное решение через
свободные неизвестные. Т.к. они могут
принимать бесконечно много числовых
значений, то у системы существует
бесконечно много численных решений.
.
Полученная система является крамеровской
и имеет единственное решение через
свободные неизвестные. Т.к. они могут
принимать бесконечно много числовых
значений, то у системы существует
бесконечно много численных решений.
На практике обычно для решения СЛАУ применяют метод Гаусса, в основе которого лежит приведение расширенной матрицы системы к трапециевидной.
Прямым ходом метода Гаусса называется приведение исходной матрицы системы к трапециевидной, обратным – нахождение неизвестных.
Если последнее уравнение содержит одно неизвестное или ни одного и правая часть равна 0, то система будет определённой, иначе – неопределённой.
СЛАУ называется однородной, если правая часть её нулевая, иначе – неоднородной.
Решения этих систем обладают следующими свойствами:
Однородная система всегда совместна и имеет решение
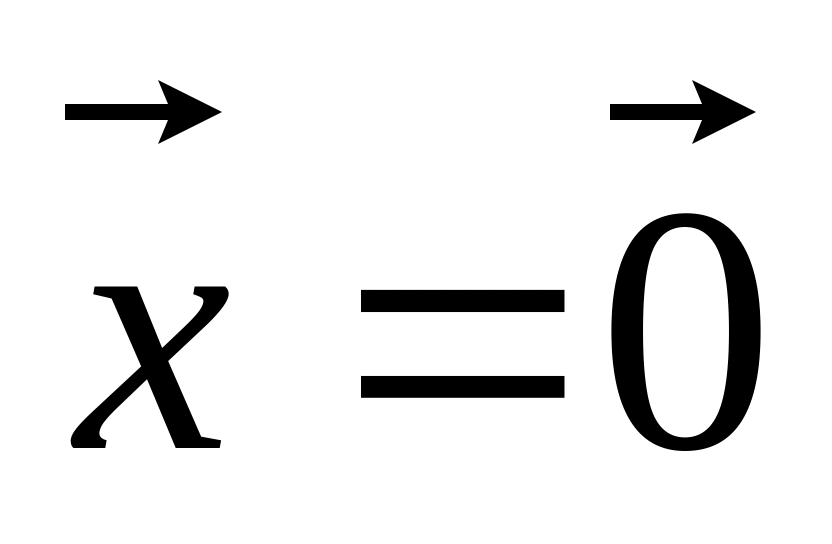 .
.Если
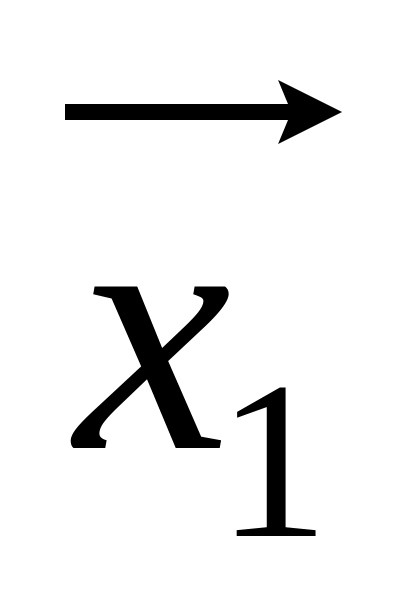 и
и
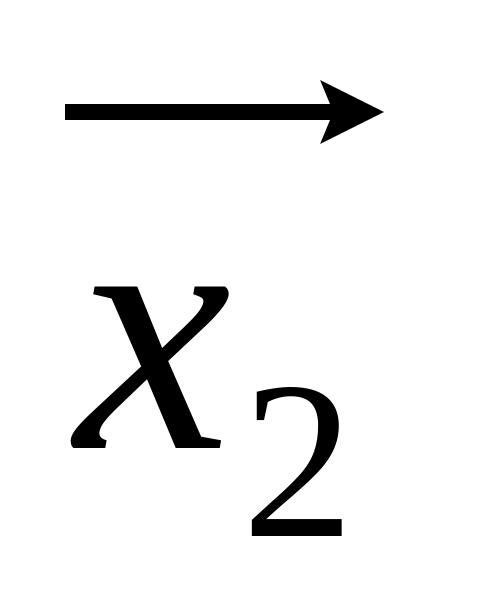 – решения системы
– решения системы
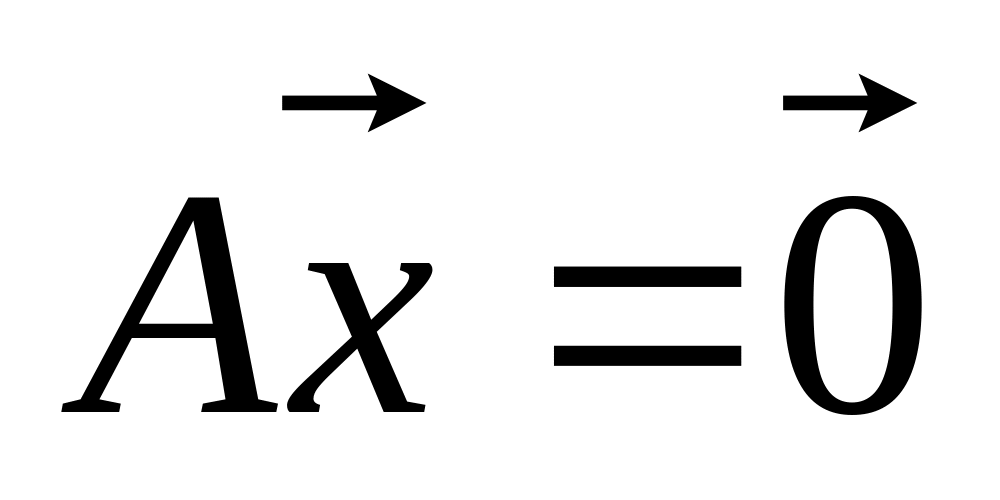 ,
то
,
то
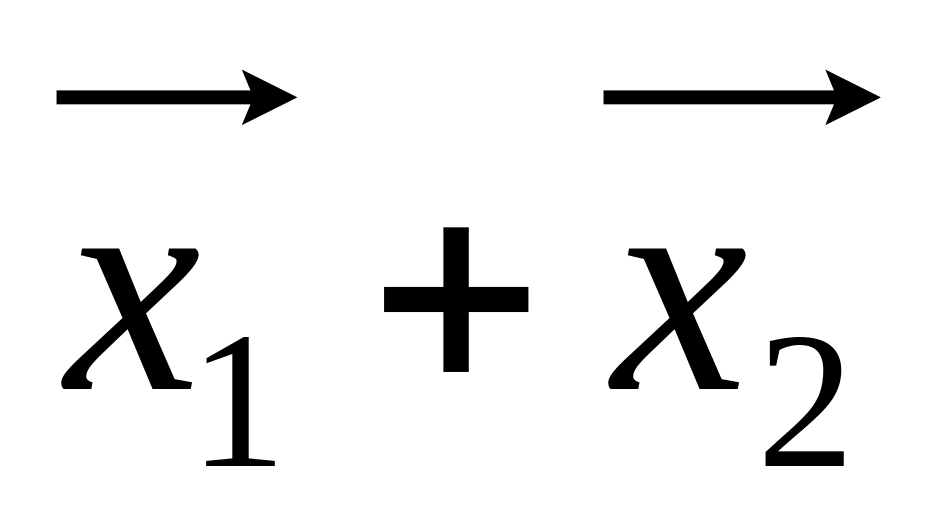 – также решение системы.
– также решение системы.Если – решение однородной системы, то
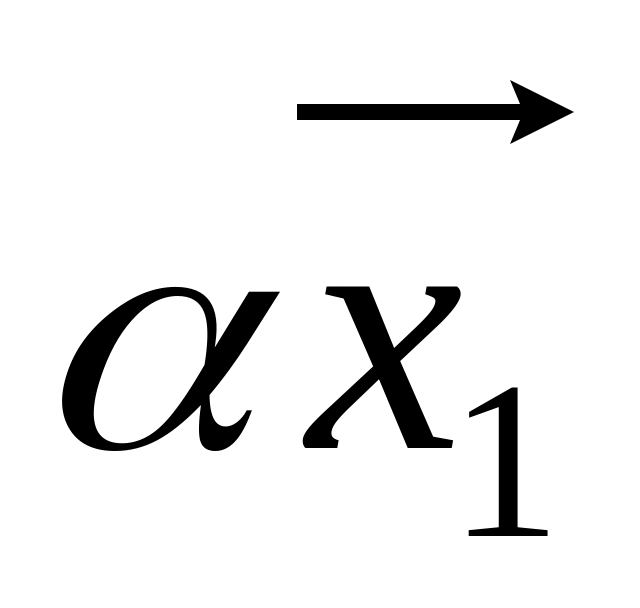 – тоже решение той же системы.
– тоже решение той же системы.
Если
![]() – решения однородной системы, то и любая
их линейная комбинация также будет
решением этой системы.
– решения однородной системы, то и любая
их линейная комбинация также будет
решением этой системы.
Решения однородной системы называют фундаментальными, если они линейно независимы и любое решение однородной системы может быть выражено через них.
Теорема о фундаментальной совокупности
решений: Пусть дана система
![]() .
Если ранг r
однородной системы
меньше числа неизвестных n,
то система имеет фундаментальную
совокупность, состоящую из
.
Если ранг r
однородной системы
меньше числа неизвестных n,
то система имеет фундаментальную
совокупность, состоящую из
![]() решений.
решений.
Рассмотрим систему
![]() .
Не умаляя общности решения, будем
считать, что базисный минор располагается
в первых r строках и
в первых r столбцах.
Соответственно, первые r
уравнений и первые r
неизвестных будут базисными.
.
Не умаляя общности решения, будем
считать, что базисный минор располагается
в первых r строках и
в первых r столбцах.
Соответственно, первые r
уравнений и первые r
неизвестных будут базисными.
![]() .
Решая эту систему методом Гаусса, выразим
базисные неизвестные через свободные.
В результате общее решение системы
будет иметь вид:
.
Решая эту систему методом Гаусса, выразим
базисные неизвестные через свободные.
В результате общее решение системы
будет иметь вид:
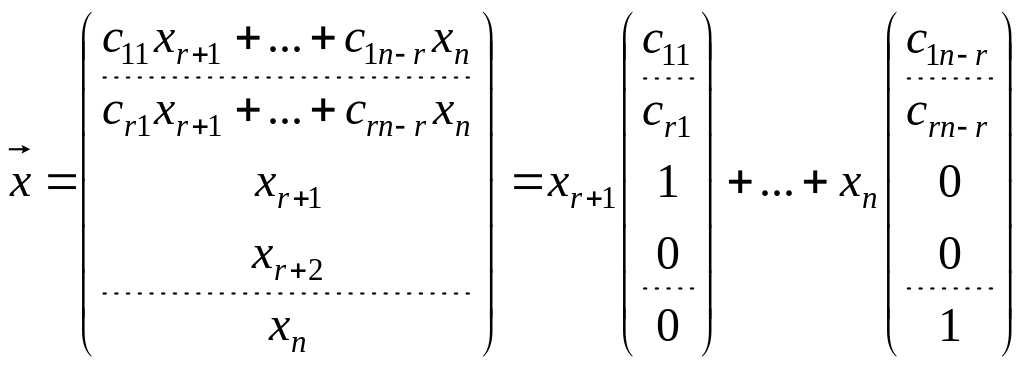 .
Покажем, что фундаментальной совокупностью
решений являются столбцы
.
Покажем, что фундаментальной совокупностью
решений являются столбцы
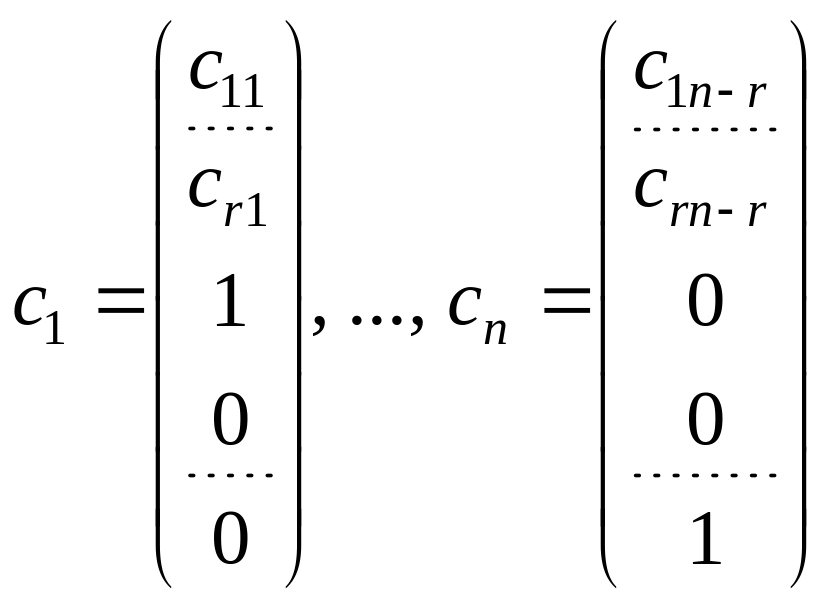 .
Пусть
.
Пусть
![]() – решение однородной системы при
– решение однородной системы при
![]() .
Видно, что ранг базисного минора матрицы
.
Видно, что ранг базисного минора матрицы
 равен
равен
![]() система имеет
линейно независимых решений.
система имеет
линейно независимых решений.
Если
![]() ,
то система имеет только одно тривиальное
решение, если
,
то система имеет только одно тривиальное
решение, если
![]() ,
то система имеет бесчисленное множество
решений.
,
то система имеет бесчисленное множество
решений.
Структура общего решения однородной системы:
Решая общую систему так же, как и
неоднородную, получим:
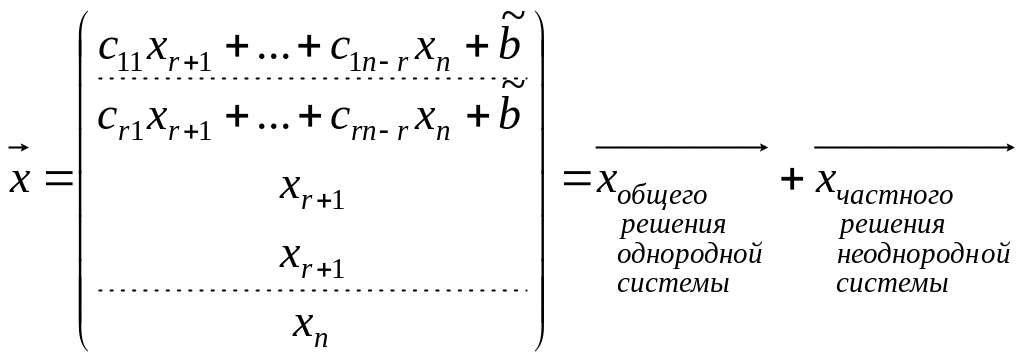 .
.
