
- •II семестр
- •Элементарные преобразования матрицы
- •Ранг матрицы
- •Системы линейных алгебраических уравнений
- •Линейные пространства.
- •Линейная зависимость и линейная независимость векторов линейных пространств.
- •Подпространство линейного пространства
- •Ядро, образ, ранг, дефект.
- •Операторы простой структуры
- •Координаты вектора в ортонормированном базисе
- •Матрица Грама
- •Ортогональное дополнение к подпространству
- •Ортогональные операторы
- •Самосопряжённые операторы
- •Квадратичная форма
- •Канонический вид квадратичной формы
- •Знакопостоянные квадратичные формы
- •Приведение общего уравнения кривой второго порядка к каноническому виду
Операторы простой структуры
Линейный оператор
называется оператором простой структуры,
если он имеет n
линейно независимых собственных
векторов. Он так называется потому, что
в базисе из собственных векторов матрица
этого оператора имеет диагональный
вид. Действительно: пусть
![]() – линейно независимые собственные
векторы оператора A.
Они образуют базис в пространстве
.
Построим матрицу оператора в этом
базисе:
– линейно независимые собственные
векторы оператора A.
Они образуют базис в пространстве
.
Построим матрицу оператора в этом
базисе:
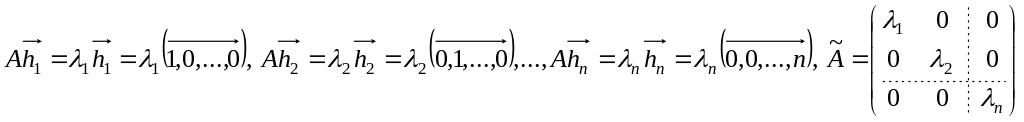 .
.
Если в каком-либо базисе
матрица оператора имеет диагональный
вид
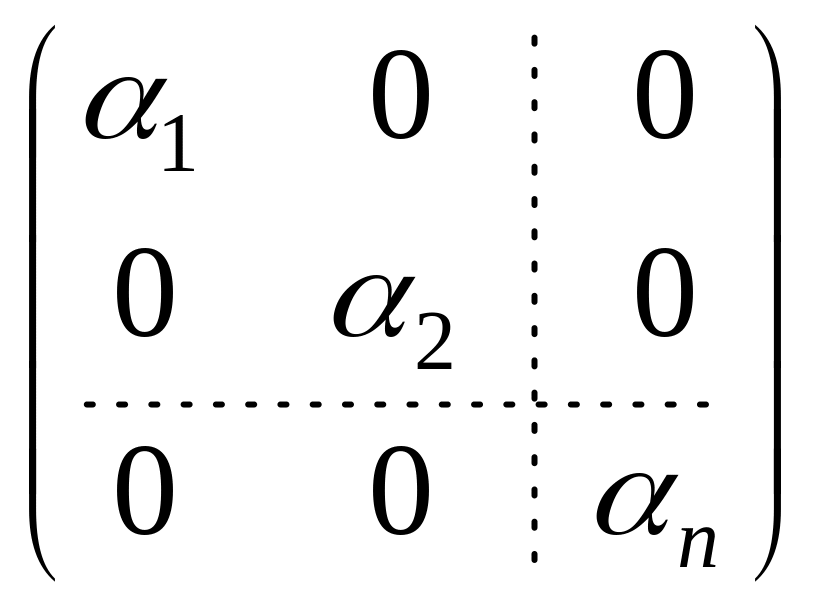 ,
где не все
различные, то векторы базиса являются
собственными для оператора A.
,
где не все
различные, то векторы базиса являются
собственными для оператора A.
Если
![]() – различные собственные числа оператора
(т.е.
– различные собственные числа оператора
(т.е.
![]() для
для
![]() ),
то соответствующие им собственные
векторы образуют линейно независимую
систему.
),
то соответствующие им собственные
векторы образуют линейно независимую
систему.
Пусть
![]() – собственное число,
– собственное число,
![]() – собственный вектор. Тогда
и
– собственный вектор. Тогда
и
![]() – линейно независимая система,
следовательно, для k
= 1 теорема верна. Пусть теперь теорема
верна для k – 1
собственного числа. Докажем тогда, что
– линейно независимая система,
следовательно, для k
= 1 теорема верна. Пусть теперь теорема
верна для k – 1
собственного числа. Докажем тогда, что
![]() только при
только при
![]() ,
т.е. векторы
– линейно независимые. Подействуем на
обе части этого уравнения оператором
,
т.е. векторы
– линейно независимые. Подействуем на
обе части этого уравнения оператором
![]() ,
что равносильно
,
что равносильно
![]() .
Домножим первое уравнение на
.
Домножим первое уравнение на
![]() .
Вычтем из предпоследнего уравнения
последнее:
.
Вычтем из предпоследнего уравнения
последнее:
![]() .
В силу линейной независимости
.
В силу линейной независимости
![]() можно утверждать, что это равенство
выполняется только при
можно утверждать, что это равенство
выполняется только при
![]()
![]() ,
а т.к.
,
а т.к.
![]() при k
i по условию и
при k
i по условию и
![]() ,
т.к. это собственные числа, то
,
т.к. это собственные числа, то
![]() .
Тогда
.
Тогда
![]() ,
т.к. линейно независимы.
,
т.к. линейно независимы.
Если линейный оператор имеет n собственных чисел, то он – оператор простой структуры.
Инвариантные подпространства
Подпространство
![]() называется инвариантным относительно
оператора A,
если для
называется инвариантным относительно
оператора A,
если для
![]() будет
будет
![]() .
.
Пусть
![]() – собственные векторы оператора
.
Тогда линейная оболочка этих векторов
является инвариантным подпространством
относительно оператора A.
– собственные векторы оператора
.
Тогда линейная оболочка этих векторов
является инвариантным подпространством
относительно оператора A.
Евклидово пространство
Линейное пространство
называется евклидовым, если в нём задано
правило, по которому каждым двум векторам
из
ставится в соответствие число. Обозначение:
![]() .
Причём для этого правила должны
выполняться три условия:
.
Причём для этого правила должны
выполняться три условия:
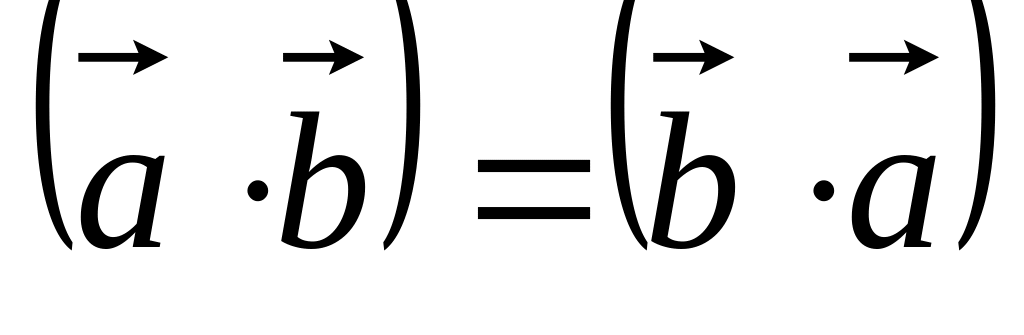 .
.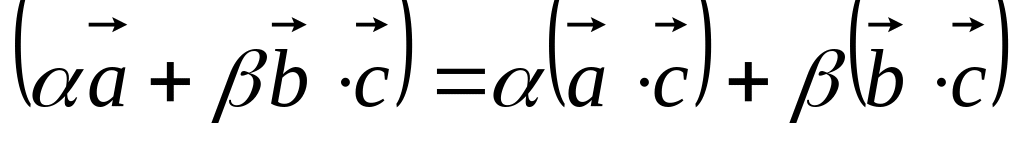 .
.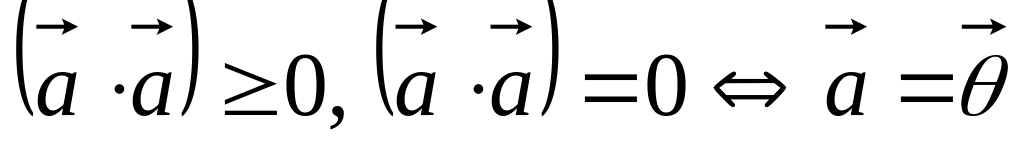 .
.
Это число называется
скалярным произведением, а евклидово
пространство размерности n
обозначается
![]() .
.
Пример: {![]() интегрируемы на
интегрируемы на
![]() }.
Тогда
}.
Тогда
![]() .
.
Ортогональные векторы
Два вектора
и
называются ортогональными, если
![]() .
.
Если в предыдущем примере
![]() ,
то sin x
и cos x ортогональны.
,
то sin x
и cos x ортогональны.
Нормой элемента
![]() называют число
называют число
![]() .
.
Для нашего примера
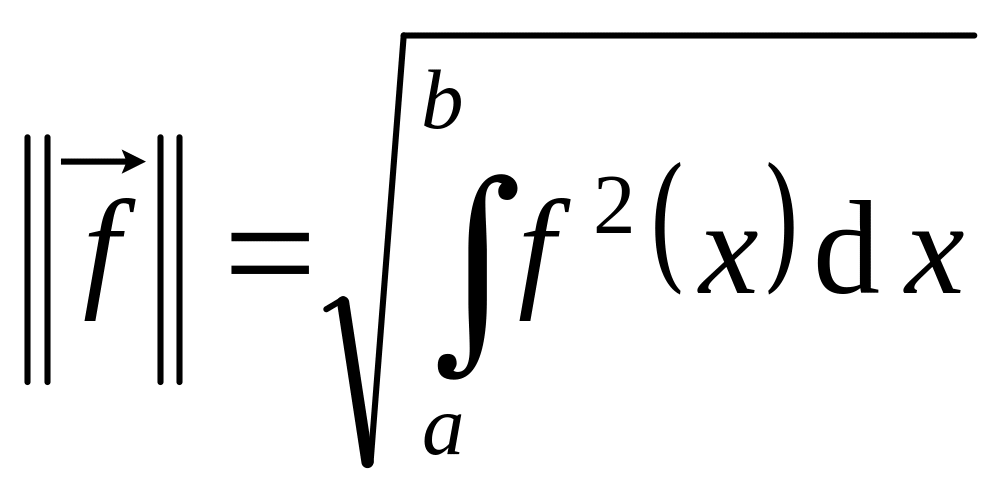 .
.
Теорема Пифагора: Если
![]() ,
то
,
то
![]() .
.
![]() ,
т.к.
.
,
т.к.
.
Неравенство Коши-Буняковского:
![]() .
.
Рассмотрим
![]() для
для
![]() .
.
Неравенство треугольника:
![]() .
.
![]() .
.
Угол между векторами
Углом между векторами
и
называют число
![]() .
.
Система векторов называется ортогональной, если векторы этой системы попарно ортогональны.
Ортогональная система ненулевых векторов является линейно независимой.
Пусть
![]() – ортогональная система векторов и
пусть
– ортогональная система векторов и
пусть
![]() ,
где
,
где
![]() – числа. Умножим обе части этого равенства
на
– числа. Умножим обе части этого равенства
на
![]() .
Тогда
.
Тогда
![]() или
или
![]()
![]() .
Аналогично для
.
Аналогично для
![]() – линейно независимая система.
– линейно независимая система.
Ортогональная система векторов называется ортонормированной, если нормы всех векторов равны единице.
Базис в евклидовом пространстве называется ортонормированным, если он составлен из ортонормированной системы векторов.
