
- •1.Система действительных чисел и операции над числами. Обыкновенные и десятичные дроби. Действия с дробями.
- •2.Иррациональные уравнения. Решение иррациональных уравнений.
- •3.Определители 2 и 3 порядка. Решение систем линейных уравнений по формулам Крамера. Основные случаи решений системы линейных уравнений.
- •4.Числовая последовательность. Постоянная и переменная величина. Монотонность и ограниченность последовательности. Бесконечно малая и бесконечно большая величина.
- •6.Числовая функция. Способы задания функций. Основные свойства функций.
- •8.Корень n-ой степени и его свойства.
- •10. Понятие логарифма. Основное логарифмическое тождество. Натуральные и десятичные логарифмы. Основные свойства логарифмов. Формула перехода от одного основания логарифма к другому.
- •11.Логарифмическая функция. Свойства и график функции
- •12.Показательная функция. Свойства и график функции
- •13.Решение показательных уравнений и неравенств.
- •14. Решение логарифмических уравнений и неравенств
- •18.Свойства и график
- •19.Свойства и график
- •27. Аксиомы стереометрии и следствия из них. (Следствие доказать(по выбору)
- •28. Взаимное расположение двух прямых в пространстве. Признак скрещивающихся прямых (вывод).
- •29. Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости (вывод)
- •30. Взаимное расположение двух плоскостей в пространстве. Признак параллельности плоскостей (вывод)
- •31. Параллельное проектирование. Свойства параллельных проекций. Изображение фигур в стереометрии.
- •32. Ортогональное проектирование. Расстояние от точки до плоскости. Симметрия в пространстве.
- •35. Двугранный угол. Угол между плоскостям. Трёхгранный угол. Многогранный угол.
- •56. Многогранник. Основные понятия. Правильные многогранники.
- •75. Площадь поверхности сферы.
- •36. Векторы в пространстве. Действия над векторами. Компланарность векторов. Разложение вектора по трем некомпланарным векторам.
- •37. Декартовы координаты. Действия над векторами, заданными координатами. Формулы для вычисления длины вектора, угла между векторами.
- •Формулы для вычисления длины вектора.
- •Формулы для вычисления угла между векторами.
- •38. Уравнение прямой на плоскости. Общее уравнение прямой, векторное, каноническое, уравнение прямой в отрезках; уравнение прямой, заданной двумя точками. Уравнение прямой на плоскости
- •Уравнение прямой в отрезках
- •Каноническое уравнение
- •Уравнение прямой, проходящей через две данные точки
- •39. Уравнение окружности. Координаты центра окружности.
- •40. Параллельность и перпендикулярность прямых, заданных уравнениями.
- •41. Приращение аргумента и приращение функции. Понятие производной функции. Вычисление производной по 4 действиям.
- •42. Геометрический и физический смысл производной. Уравнение касательной к графику функции.
- •1)Физический смысл производной.
- •2) Геометрический смысл производной.
- •43. Правило дифференцирования суммы двух функций, произведения двух функций, частного двух функций.
- •45. Понятие сложной функции. Правило дифференцирования сложной функции.
- •46. Производные тригонометрических функций.
- •47. Производная показательной и логарифмической функции.
- •59. Пирамида. Основные элементы: основание, боковое ребро, высота, боковая грань. Правильная пирамида. Усеченная пирамида.
- •60. Фигура вращения. Цилиндр. Сечения цилиндра плоскостью.
- •61. Конус. Усеченный конус. Сечение конуса плоскостями.
- •62. Шар. Сфера. Уравнение сферы.
- •63. Сечения сферы, шара плоскостью. Плоскость, касательная к сфере.
- •64. Понятие объема тела. Общие свойства объемов многогранников.
- •65. Объем прямоугольного параллелепипеда. Объем произвольной призмы (вывод).
- •66. Объем пирамиды (вывод). Объем усеченной пирамиды.
- •67. Объем цилиндра (вывод)
- •69. Объем конуса(вывод). Объем усеченного конуса.
- •70. Объем шара (вывод). Объем шарового сектора, объем шарового сегмента.
- •49. Критические точки функции. Теорема существования экстремумов функции.
- •57. Призма. Основные элементы: основания, боковое ребро, высота, боковая грань, диагональ, диагональное сечение. Правильная призма.
- •58. Параллелепипед и его свойства.
- •33. Угол между прямой и плоскостью. Теорема о трёх перпендикулярах (доказать)
- •34. Перпендикулярность прямой и плоскости. Признак препендикулярности прямой и плоскости (доказать).
57. Призма. Основные элементы: основания, боковое ребро, высота, боковая грань, диагональ, диагональное сечение. Правильная призма.
Призмой называется
многогранник, который состоит из двух
плоских многоугольников, лежащих в
разных плоскостях и совмещаемых
параллельным переносом, и всех отрезков,
соединяющих соответствующие точки этих
многоугольников. Многоугольники
называются основаниями
призмы, а
отрезки, соединяющие соответствующие
вершины, - боковыми
ребрами призмы.
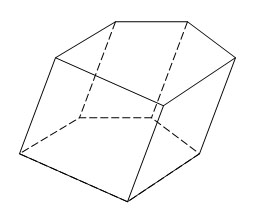 Свойства
призмы:
1.
Основания призмы равны и лежат в
параллельных плоскостях.
2.
Боковые ребра параллельны и
равны.
Поверхность
призмы состоит
из оснований и боковой поверхности. Боковая
поверхность состоит
из параллелограммов. Высотой
призмы называется
расстояние между плоскостями. Отрезок,
соединяющий две вершины призмы, не
принадлежащие одной грани,
называется диагональю
призмы.
Свойства
призмы:
1.
Основания призмы равны и лежат в
параллельных плоскостях.
2.
Боковые ребра параллельны и
равны.
Поверхность
призмы состоит
из оснований и боковой поверхности. Боковая
поверхность состоит
из параллелограммов. Высотой
призмы называется
расстояние между плоскостями. Отрезок,
соединяющий две вершины призмы, не
принадлежащие одной грани,
называется диагональю
призмы.
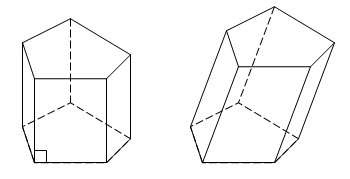 Призма
называется прямой,
если ее боковые ребра перпендикулярны
основаниям.
Призма
называется наклонной,
если ее боковые ребра не перпендикулярны
основаниям.
У
прямой призмы грани – прямоугольники.
Призма
называется прямой,
если ее боковые ребра перпендикулярны
основаниям.
Призма
называется наклонной,
если ее боковые ребра не перпендикулярны
основаниям.
У
прямой призмы грани – прямоугольники.
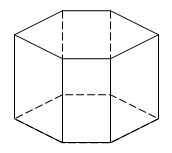 Призма
называется правильной,
если ее основания являются правильными
многоугольниками.
Площадью
боковой поверхности призмы называется
сумма площадей боковых граней.
Полная
поверхность призмы равна
сумме боковой поверхности и площадей
оснований
Призма
называется правильной,
если ее основания являются правильными
многоугольниками.
Площадью
боковой поверхности призмы называется
сумма площадей боковых граней.
Полная
поверхность призмы равна
сумме боковой поверхности и площадей
оснований
58. Параллелепипед и его свойства.
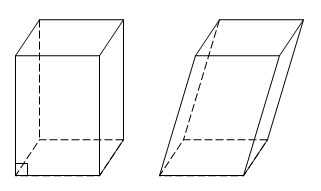 Параллелепипедом
называется призма, в основании которой
параллелограмм.
Параллелепипед
называется прямым, если его
боковые ребра перпендикулярны
основаниям.
Параллелепипед
называется наклонным, если его
боковые ребра не перпендикулярны
основаниям.
Грани параллелепипеда,
не имеющие общих вершин,
называются противолежащими.
Параллелепипедом
называется призма, в основании которой
параллелограмм.
Параллелепипед
называется прямым, если его
боковые ребра перпендикулярны
основаниям.
Параллелепипед
называется наклонным, если его
боковые ребра не перпендикулярны
основаниям.
Грани параллелепипеда,
не имеющие общих вершин,
называются противолежащими.
У параллелепипеда
противолежащие грани параллельны и
равны.
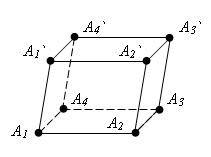 Доказательство
Возьмем
любые две противолежащие грани
параллелепипеда: A1A2A2`A1` и A3A4A4`A3`. Так как
все грани параллелепипеда – параллелограммы,
то прямая A1A2 параллельна прямой A4A3, а
прямая A1A1` параллельна прямой A4A4`.
Следовательно плоскости рассматриваемых
граней параллельны.
Так как грани
параллелепипеда – параллелограммы, то
отрезки A1A4, A1`A4`, A2`A3` и A2A3 – параллельны
и равны. Следовательно грань A1A2A2`A1`
совмещается параллельным переносом
вдоль ребра A1A4 с гранью A3A4A4`A3` и, значит,
грани равны.
Точно также доказывается
параллельность и равенство других
противолежащих граней параллелепипеда.
Теорема доказана.
Доказательство
Возьмем
любые две противолежащие грани
параллелепипеда: A1A2A2`A1` и A3A4A4`A3`. Так как
все грани параллелепипеда – параллелограммы,
то прямая A1A2 параллельна прямой A4A3, а
прямая A1A1` параллельна прямой A4A4`.
Следовательно плоскости рассматриваемых
граней параллельны.
Так как грани
параллелепипеда – параллелограммы, то
отрезки A1A4, A1`A4`, A2`A3` и A2A3 – параллельны
и равны. Следовательно грань A1A2A2`A1`
совмещается параллельным переносом
вдоль ребра A1A4 с гранью A3A4A4`A3` и, значит,
грани равны.
Точно также доказывается
параллельность и равенство других
противолежащих граней параллелепипеда.
Теорема доказана.
33. Угол между прямой и плоскостью. Теорема о трёх перпендикулярах (доказать)
Прямая a пересекает плоскость α. а не перпендикулярна плоскости. Основания перпендикуляров, опущенных из точек прямой a на плоскость α, лежат на прямой a`. Эта прямая называется проекцией прямой a на плоскость α. Угол между прямой и проекцией этой прямой на плоскость называется углом между прямой и плоскостью.
|
||
|

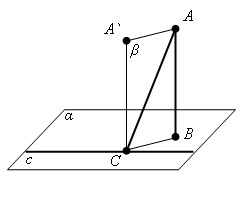 Доказательство.
Пусть
AB – перпендикуляр к плоскости α,
AC – наклонная и с – прямая в
плоскости α, проходящая через
основание С наклонной. Проведем
прямую CA` параллельную прямой AB.
Она перпендикулярна плоскости α.
Проведем через прямые AB и A`C плоскость
β. Прямая с перпендикулярна прямой
CA`. Если она перпендикулярна прямой
CB, то она перпендикулярна плоскости
α, а значит, и прямой AC.
Доказательство.
Пусть
AB – перпендикуляр к плоскости α,
AC – наклонная и с – прямая в
плоскости α, проходящая через
основание С наклонной. Проведем
прямую CA` параллельную прямой AB.
Она перпендикулярна плоскости α.
Проведем через прямые AB и A`C плоскость
β. Прямая с перпендикулярна прямой
CA`. Если она перпендикулярна прямой
CB, то она перпендикулярна плоскости
α, а значит, и прямой AC.