
- •1. Понятие реш задач мат программирования. Постановка задач линейного программирования. Примеры. 1.
- •2 . Основные формы задача лп. Правило сведения злп к канон форме. Геометр интерпр злп. Понятие угловой точки мн-ва
- •3. Критерий угловой точки множества.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными злп.
- •7. Построение симплекс-таблицы. Достаточное условие оптимизации в задаче лп. Достаточное условие неразрешимости задачи лп.
- •8. Итерация симплекс-метода.
- •9. Обоснование конечности симплекс-алгоритма.
- •10. Обоснование непустоты множества планов в злп. Пример.
- •11.Нахождение базиса угловой точки. Пример. Св-во решений злп.
- •12. Свой-ва решений злп.
- •13. Постановка тз. Построение плана перевозок методом северо-западного угла.
- •14.Определение закрытой модели тз. Критерий существования решения тз.
- •Замечание Транспортная задача, для которой выполняется условие (1) называется закрытой, в противном случае – открытой.
- •15.Исследование множества клеток транспортной таблицы.
- •16.Достаточное условие минимальности стоимости перевозок
- •17. Определения выпуклого множества, выпуклой функции. Свойства выпуклых множеств. Сумма выпуклых функций. Свойство Лебега выпуклых функций. Свойство неотрицательности остатка выпуклой функции.
- •18. Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции.
- •20.Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •21.Метод исключения решения задачи на усл минимум. Пример.
- •23.Классич правило мн л в задаче опт-ции с огранич типа равенств. Необходим условия первого и второго порядка в задаче опт-ции типа равенств.
- •24.Достат условия экстремума в задаче опт-ции с ограничениями типа равенств.
- •25. Задача проектирования на выпуклое и замкнутое множество. Свойства проекции. Примеры.
- •27. Основные определения в задаче одномерной минимизации. Примеры.
- •Пример . Множ-во решений задачи min-ции f(X)
- •28.Метод деления отрезка пополам решения задачи одномерной минимизации.
- •29.Метод золотого сечения.
- •30.Метод ломаных. Обоснование и алгоритм. Пример.
- •31.Обоснование сходимости метода ломаных решения задачи одомерной минимизации
- •33. Алгоритм метода условного градиента
- •Теорема3
- •35. Сходимостсь метода скорейшого спуска
- •36. Постановка задачи вариационного исчисления. Пр.
- •Определим множество:
- •Замечание
- •37. Метод вариаций лагранжа Пусть в задаче , где и исследуется на минимум кривая , тогда все допустимые кривые X(t), из множества X можно представить в виде:
- •38. Уравнение Эйлера.
- •39. Случай интегрируемости ур-ния Эйлера. Пример.
- •40. Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •41. Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования.
- •42. Задача вариационного исчисления с движущимся по кривой коцом.
- •43. Примеры задач динамического программирования, их особенности.
- •44. Принципы динам програм и функцон ур-ния Беллмана.
- •45. Постановка задачи оптимального быстродействия.
- •46 Достат условия оптимальности для линейной задачи оптимального быстродействия (зоб).
- •47. Пример решения задач оптимального быстродействия.
21.Метод исключения решения задачи на усл минимум. Пример.
Будем
решать задачу
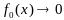 (1)
(1)
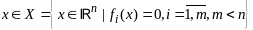 (2);
(2);
Предполаг,
сто ф-ции
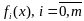 пределены и имеют непрепывн частные
производные 1-го порядка на всем
пространстве
.
Ограничение (2) наз ограничениями типа
равенств.
пределены и имеют непрепывн частные
производные 1-го порядка на всем
пространстве
.
Ограничение (2) наз ограничениями типа
равенств.
Если
систему ограничений (2) можно представить
в виде
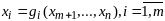 ,
то задачу (1),(2) можно свести к задаче
безусловной оптимизации ф-ции
,
то задачу (1),(2) можно свести к задаче
безусловной оптимизации ф-ции
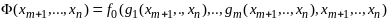 ,
зависящей от (n-m)
переменных.
,
зависящей от (n-m)
переменных.
Теоретич возможность применения такого метода исключения для реш задачи учл оптимизации основана на теореме о неявных ф-циях.
Т1
о неявных ф-циях. Пусть
m-мерная
ф-ция
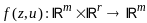 определена и непрерывна по всем
переменным, диф-ма по переменным z
и удовлетворяет условиям: в точке
определена и непрерывна по всем
переменным, диф-ма по переменным z
и удовлетворяет условиям: в точке
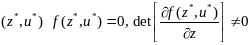 ,
тогда сущ m-мерная
ф-ция
,
тогда сущ m-мерная
ф-ция
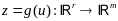 определенная и непрерывная в окрестности
точки
определенная и непрерывная в окрестности
точки
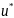 ,
такая что
,
такая что
1.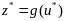
2.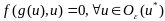
3.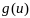 имеет
в окрестности
имеет
в окрестности
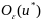 частн произ-ные того же порядка, что и
ф-ция
частн произ-ные того же порядка, что и
ф-ция
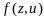 по
по
 .
.
Утверждение.
Метод искл в задаче (1),(2)применим, если
в окрестности точки
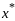 ф-ции
ф-ции
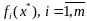 диф-мы и
диф-мы и
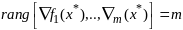 .
.
Док-во:
Матрица
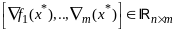 .
Т.к.
.
Т.к.
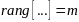 ,
то сущ минор порядка m
отличный от 0. Пусть этот минор располагается
в 1-ых m
строках рассм матрицы. Обозначим 1-ые m
координат вектора x
через z,
а остальные через u;
через
–
вектор ф-цию
,
то сущ минор порядка m
отличный от 0. Пусть этот минор располагается
в 1-ых m
строках рассм матрицы. Обозначим 1-ые m
координат вектора x
через z,
а остальные через u;
через
–
вектор ф-цию
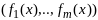 .
Тогда в точке
.
Тогда в точке
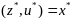 вып
все усл теоремы в неявн ф-циях,следовательно
сущ искомая ф-ция
вып
все усл теоремы в неявн ф-циях,следовательно
сущ искомая ф-ция
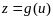
Замечание.
Практ применение мет искл сущ-но
ограничено сложностью решения в явном
виде системы ограничений
 относительно m
неизв-ных.
относительно m
неизв-ных.
Пример2.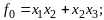
 .
.
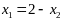 ;
;
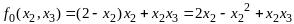 ;
;
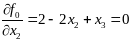 ;
;
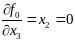
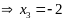
(0;-2)-стац
точка.
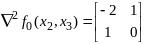
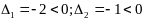
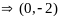 не
явл экстремальной, исх целевая ф-ция на
мн-ве Х экстремумов не имеет.
не
явл экстремальной, исх целевая ф-ция на
мн-ве Х экстремумов не имеет.
22.Обобщ правило множ Лагранжа в задаче опт-ции ф-ции с огранич типа равенств.
Класич
метод решения задачи
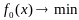 (1)
(2) связан с ф. Л.
(1)
(2) связан с ф. Л.
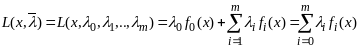
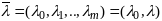
Т1
обобщ правило мн Л.
Пусть точка
 явл
точкой лок минимума ф-ции (1) при огр (2)
и ф-ции
явл
точкой лок минимума ф-ции (1) при огр (2)
и ф-ции
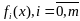 непрерывно диф-мы в окрест точки
,
тогда сущ числа
непрерывно диф-мы в окрест точки
,
тогда сущ числа
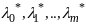 одновременно
одновременно
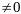 ,
наз-мые множителями Л, такие что
,
наз-мые множителями Л, такие что
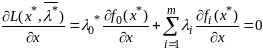 (3).
Док-во.
Т.к. числа
одновременно в 0 не обращаются, то вектора
(3).
Док-во.
Т.к. числа
одновременно в 0 не обращаются, то вектора
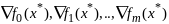 явл линейно зависимыми. Допустим
противное, т.е. перечисленные вектора
явл лин незав, тогда их кол-во не
превосходит размерности пр-ва, т.е.
явл линейно зависимыми. Допустим
противное, т.е. перечисленные вектора
явл лин незав, тогда их кол-во не
превосходит размерности пр-ва, т.е.
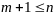 ,
если
,
если
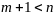 ,
то систему перечисленных векторов
дополним векторами
,
то систему перечисленных векторов
дополним векторами
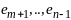 т. о., чтобы система
т. о., чтобы система
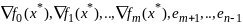 – лин незав. Введем ф-цию
– лин незав. Введем ф-цию
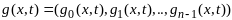 след образом
след образом
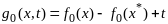 ,
,
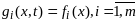 ;
;
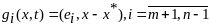 .
Для нее вып
.
Для нее вып
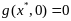 и определитель
и определитель
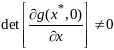 для ф-ции
для ф-ции
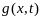 вып-ны усл теоремы о неявных ф-циях.
,
системы уравнений
вып-ны усл теоремы о неявных ф-циях.
,
системы уравнений
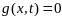 имеют решение
имеют решение
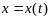 ,
определенные
,
определенные
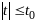 ,
где
,
где
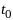 –некот малое число и это решение удовл
след усл 1
–некот малое число и это решение удовл
след усл 1
 ;
2
;
2
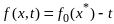 ,
,
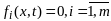 (*);
(*);
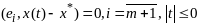 .
Найденная ф-ция
.
Найденная ф-ция
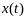 явл непрер диф-мой для
.
Заметим, что ф-ция
удовлетв ограничениям (2) (следует из
(*)), и при
явл непрер диф-мой для
.
Заметим, что ф-ция
удовлетв ограничениям (2) (следует из
(*)), и при
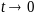
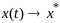 (след из
(след из
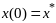 ).
Рассм знач целев ф-ции
).
Рассм знач целев ф-ции
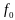 на ф-ции
для
на ф-ции
для
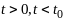 :
: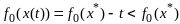 .
Мы нашли другую точку
,
в кот значение целевой ф-ции < чем
значение
.
Мы нашли другую точку
,
в кот значение целевой ф-ции < чем
значение
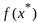 ,
что противоречит лок оптимальности
точки
,
что противоречит лок оптимальности
точки
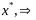 ,
предполож о лин независимости векторов
неверно.
Зам1.
Из Т1
,
что в задаче (1),(2) оптим могут быть только
те точки
,
для кот сущ ненулевой вектор множителей
Л.
,
предполож о лин независимости векторов
неверно.
Зам1.
Из Т1
,
что в задаче (1),(2) оптим могут быть только
те точки
,
для кот сущ ненулевой вектор множителей
Л.
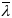 ,
что точка
,
что точка
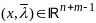 удовлетвор системе из n+m
уравнений:
удовлетвор системе из n+m
уравнений: (4).
Зам2 Если
точка
(4).
Зам2 Если
точка
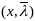 предст собой решение
системы (4), то точка
предст собой решение
системы (4), то точка
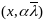 для
для
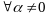 тоже предст собой решение системы (4),
т.е мн.Л. опред с точностью до постоян
множителя. Поэтому при реш системы
соотнош (4) знак одной их координат
обобщенного вектора Л. можно выбрать
заранее. Обычно полагают
тоже предст собой решение системы (4),
т.е мн.Л. опред с точностью до постоян
множителя. Поэтому при реш системы
соотнош (4) знак одной их координат
обобщенного вектора Л. можно выбрать
заранее. Обычно полагают
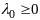 .
Опр.
Если сист. (4) имеет только такие решения,
что
.
Опр.
Если сист. (4) имеет только такие решения,
что
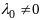 ,
то задачу (1),(2) наз нормальной (регулярной,
невырожденной). Зам3.
В норм задаче множитель
,
то задачу (1),(2) наз нормальной (регулярной,
невырожденной). Зам3.
В норм задаче множитель
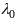 полагают =1. Зам4.
Решив систему соотнош (4), находят точки
подозрительные на экстремум. Для
выяснения того, будут ли найд точки
экстремальными, проводят допол исследов
с исп 2-ых производных ф-ции Л. по переменным
.
полагают =1. Зам4.
Решив систему соотнош (4), находят точки
подозрительные на экстремум. Для
выяснения того, будут ли найд точки
экстремальными, проводят допол исследов
с исп 2-ых производных ф-ции Л. по переменным
.
