
- •1. Понятие реш задач мат программирования. Постановка задач линейного программирования. Примеры. 1.
- •2 . Основные формы задача лп. Правило сведения злп к канон форме. Геометр интерпр злп. Понятие угловой точки мн-ва
- •3. Критерий угловой точки множества.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными злп.
- •7. Построение симплекс-таблицы. Достаточное условие оптимизации в задаче лп. Достаточное условие неразрешимости задачи лп.
- •8. Итерация симплекс-метода.
- •9. Обоснование конечности симплекс-алгоритма.
- •10. Обоснование непустоты множества планов в злп. Пример.
- •11.Нахождение базиса угловой точки. Пример. Св-во решений злп.
- •12. Свой-ва решений злп.
- •13. Постановка тз. Построение плана перевозок методом северо-западного угла.
- •14.Определение закрытой модели тз. Критерий существования решения тз.
- •Замечание Транспортная задача, для которой выполняется условие (1) называется закрытой, в противном случае – открытой.
- •15.Исследование множества клеток транспортной таблицы.
- •16.Достаточное условие минимальности стоимости перевозок
- •17. Определения выпуклого множества, выпуклой функции. Свойства выпуклых множеств. Сумма выпуклых функций. Свойство Лебега выпуклых функций. Свойство неотрицательности остатка выпуклой функции.
- •18. Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции.
- •20.Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •21.Метод исключения решения задачи на усл минимум. Пример.
- •23.Классич правило мн л в задаче опт-ции с огранич типа равенств. Необходим условия первого и второго порядка в задаче опт-ции типа равенств.
- •24.Достат условия экстремума в задаче опт-ции с ограничениями типа равенств.
- •25. Задача проектирования на выпуклое и замкнутое множество. Свойства проекции. Примеры.
- •27. Основные определения в задаче одномерной минимизации. Примеры.
- •Пример . Множ-во решений задачи min-ции f(X)
- •28.Метод деления отрезка пополам решения задачи одномерной минимизации.
- •29.Метод золотого сечения.
- •30.Метод ломаных. Обоснование и алгоритм. Пример.
- •31.Обоснование сходимости метода ломаных решения задачи одомерной минимизации
- •33. Алгоритм метода условного градиента
- •Теорема3
- •35. Сходимостсь метода скорейшого спуска
- •36. Постановка задачи вариационного исчисления. Пр.
- •Определим множество:
- •Замечание
- •37. Метод вариаций лагранжа Пусть в задаче , где и исследуется на минимум кривая , тогда все допустимые кривые X(t), из множества X можно представить в виде:
- •38. Уравнение Эйлера.
- •39. Случай интегрируемости ур-ния Эйлера. Пример.
- •40. Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •41. Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования.
- •42. Задача вариационного исчисления с движущимся по кривой коцом.
- •43. Примеры задач динамического программирования, их особенности.
- •44. Принципы динам програм и функцон ур-ния Беллмана.
- •45. Постановка задачи оптимального быстродействия.
- •46 Достат условия оптимальности для линейной задачи оптимального быстродействия (зоб).
- •47. Пример решения задач оптимального быстродействия.
3. Критерий угловой точки множества.
Рассмотрим
задачу в канонической форме:
 (1),
(1),
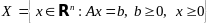 (2).
(2).
Опр.
Угловой точкой мн-ва
 называется точкой
называется точкой
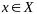 которая не может быть представлена как
точка отрезка
которая не может быть представлена как
точка отрезка
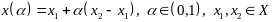 для любых
для любых
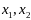 .
.
Т.(Критерий
угловой точки): Обозначим
через
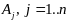 столбцы матрицы А, тогда основные
ограничения в системе (2) можно записать
в виде:
столбцы матрицы А, тогда основные
ограничения в системе (2) можно записать
в виде:
 .
Предположим, что матрица А в системе
(2) имеет
.
Предположим, что матрица А в системе
(2) имеет
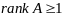 ,т.е.
матрица А ненулевая. Для того, чтобы
точка
была угловой точкой – G
необходимо и достаточно, чтобы существовали
,т.е.
матрица А ненулевая. Для того, чтобы
точка
была угловой точкой – G
необходимо и достаточно, чтобы существовали
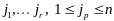 ,
что справедливо равенство: (3)
,
что справедливо равенство: (3)
 ,
если
,
если
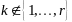 и
и
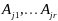 – ЛНЗ.
– ЛНЗ.
Док-во:
Необ.: Пусть
– угловая точка этого мн-ва. а)
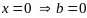 .
Т.к. м-ца А в соотнош. (2) невырождена, то
существует r
ЛНЗ векторов
.
Т.к. м-ца А в соотнош. (2) невырождена, то
существует r
ЛНЗ векторов
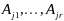 ,
то выполнено
,
то выполнено
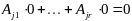 .
т.е. (3) справедливо; б)
.
т.е. (3) справедливо; б)
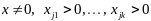 тогда основные ограничения в (2) превратятся
в равенство:
тогда основные ограничения в (2) превратятся
в равенство:
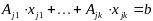 (4).
Рассм. р-во
(4).
Рассм. р-во
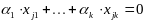 (5).
Построим точки
(5).
Построим точки
 и
и
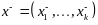 след. образом:
след. образом:
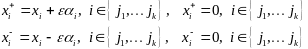
т.к.
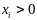 ,
то
,
то
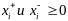
к
равенству (4) прибавим и отнимем р-во (5)
умноженное на
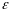 получим что выполняются равенства:
получим что выполняются равенства:
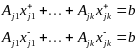 ,
т.е
,
т.е
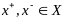 .
Легко видеть
.
Легко видеть
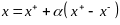 , но х – угловая точка след-но
, но х – угловая точка след-но
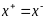 след-но
след-но
 в (5), т.е. вектора
в (5), т.е. вектора
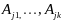 – ЛНЗ след-но
– ЛНЗ след-но

Если
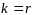 ,
то (3) – доказано, если
,
то (3) – доказано, если
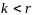 ,
то к векторам
можно добавить вектора
,
то к векторам
можно добавить вектора
 так, чтобы
так, чтобы
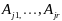 – ЛНЗ, тогда (3) примет вид:
– ЛНЗ, тогда (3) примет вид:
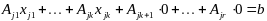 .
.
Достат.:
пусть для точки
справедливо (3):
– ЛНЗ, где
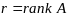 .
Предположим, что
.
Предположим, что
 ,
что
,
что
 (6).
Покажем, что (6) возможно только при
(6).
Покажем, что (6) возможно только при
 .
Рассм. нулевую координату точки х:
.
Рассм. нулевую координату точки х:
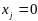 ,т.е
,т.е
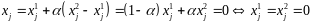 .
Докажем (6) для тех координат, которые
больше 0. Положительными координатами
точки х могут быть только те, у которых
индекс
.
Докажем (6) для тех координат, которые
больше 0. Положительными координатами
точки х могут быть только те, у которых
индекс
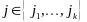 .
Пусть
.
Пусть
 Случай когда
Случай когда
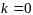 или
не исключается, тогда система основных
ограничений из (2) преобразуется к виду:
или
не исключается, тогда система основных
ограничений из (2) преобразуется к виду:
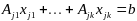 .
Докажем, что
.
Докажем, что
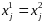 ,
если
.
Точки
,
если
.
Точки
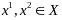 было доказано, что
было доказано, что
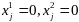 ,
когда
след-но
,
когда
след-но
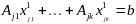 и
и
 .
Вектора
– ЛНЗ, а разложение произвольного
вектора пространства по ЛНЗ-векторам
является единственным, след-но
.
Вектора
– ЛНЗ, а разложение произвольного
вектора пространства по ЛНЗ-векторам
является единственным, след-но
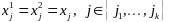 для строго положительных координат.
для строго положительных координат.
4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
Опр.
Система векторов
входящие в равенство
,
если
называется базисом угловой точки х,
координаты
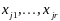 называются базисными, остальные
координаты – небазисными.
называются базисными, остальные
координаты – небазисными.
Опр. Если все базисные координаты точки х строго больше 0, тогда точка х называется невырожденной.
Следствие. Если точка х – невырожденная угловая точка, то для нее существует единственный базис. Вырожденная угловая точка может обладать несколькими базисами.
Пример:
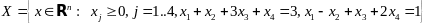
 – невырожденная
угловая точка, проверим это.
– невырожденная
угловая точка, проверим это.

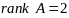 ,
,
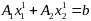 ,
где
,
где
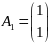 ,
,
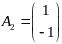 .
.
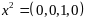 – вырожденная
угловая точка, так как при рассмотрении
равенства
– вырожденная
угловая точка, так как при рассмотрении
равенства
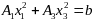 ,
где
,
где
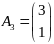 точка
точка
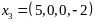 – не является угловой точкой, так как
– не является угловой точкой, так как
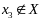 .
.
5. Связь между переменными злп.
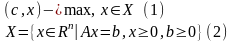
Пусть
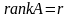 ,
,
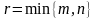 .
Из системы осн. ограничений можно удалить
ЛЗ ур-я, тогда
.
Из системы осн. ограничений можно удалить
ЛЗ ур-я, тогда
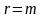 .
Если
.
Если
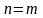 ,
то система
,
то система
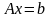 им. единств. решение. Если это реш-е не
удовл. прямым огр-ям, то
им. единств. решение. Если это реш-е не
удовл. прямым огр-ям, то
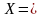 ,
иначе
,
иначе
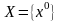 .
Рассм
.
Рассм
 .
Найдена угл. т-ка
.
Найдена угл. т-ка
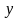 ,
,
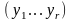 - базисные компоненты,
- базисные компоненты,
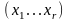 - тоже, иначе м. перенумеровать.
- тоже, иначе м. перенумеровать.
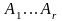 - ЛНЗ. Обозначения:
- ЛНЗ. Обозначения:
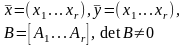
Умножим
на
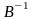 :
:
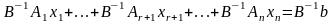
Т.к.
у – угловая, то
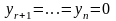 ,
т.е.
,
т.е.
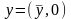 .
Рав-во
.
Рав-во
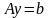 м. привести в виду
м. привести в виду
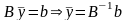 .
Из определения В
.
Из определения В
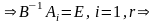 (*)
примет вид:
(*)
примет вид:
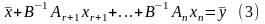 .
Из (3) выражаем
.
Из (3) выражаем
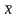 -
(4), обозначаем
-
(4), обозначаем
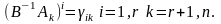
(3)
перепишем в виде: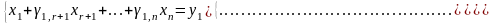 (5)
(5)
(3), (4), (5) – зависимость между базисными и небазисными переменными.
6 . Ф-ла приращения целев ф-ии для ЗЛП.
Рассм
знач целев ф-ии в некот точке
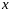 ,
т.е.
,
т.е.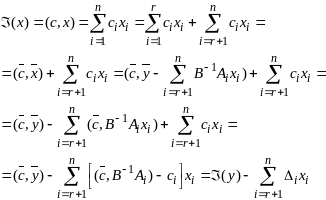 ,
где
,
где
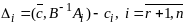
Получим
формулу (1)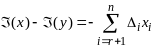 -
ф-ла приращ целев ф-ии,
-
ф-ла приращ целев ф-ии,
В-р
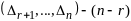 в-р оценок целевой ф-ии
в-р оценок целевой ф-ии
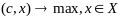
Замеч:
Величина
имеет смысл и для
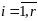 ;
действительно,
;
действительно,
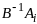 - единичный в-р
- единичный в-р
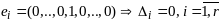
Замеч:
Вел-на
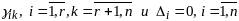 полностью опр-ся коэф-ми м-цы
полностью опр-ся коэф-ми м-цы
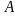 ,
в-ра
,
в-ра
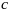 и базисом угловой точки
и базисом угловой точки
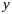 ,
при этом не зав-т от в-ра ресурсов
,
при этом не зав-т от в-ра ресурсов
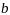
Замеч:
Из (1) виден
физический смысл оценок
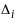 .
Величины
представляют собой взятую с обратным
знаком скорость зменения целев ф-ии при
изменении i-ой
небазисной переменной.
.
Величины
представляют собой взятую с обратным
знаком скорость зменения целев ф-ии при
изменении i-ой
небазисной переменной.
