
- •1. Понятие реш задач мат программирования. Постановка задач линейного программирования. Примеры. 1.
- •2 . Основные формы задача лп. Правило сведения злп к канон форме. Геометр интерпр злп. Понятие угловой точки мн-ва
- •3. Критерий угловой точки множества.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными злп.
- •7. Построение симплекс-таблицы. Достаточное условие оптимизации в задаче лп. Достаточное условие неразрешимости задачи лп.
- •8. Итерация симплекс-метода.
- •9. Обоснование конечности симплекс-алгоритма.
- •10. Обоснование непустоты множества планов в злп. Пример.
- •11.Нахождение базиса угловой точки. Пример. Св-во решений злп.
- •12. Свой-ва решений злп.
- •13. Постановка тз. Построение плана перевозок методом северо-западного угла.
- •14.Определение закрытой модели тз. Критерий существования решения тз.
- •Замечание Транспортная задача, для которой выполняется условие (1) называется закрытой, в противном случае – открытой.
- •15.Исследование множества клеток транспортной таблицы.
- •16.Достаточное условие минимальности стоимости перевозок
- •17. Определения выпуклого множества, выпуклой функции. Свойства выпуклых множеств. Сумма выпуклых функций. Свойство Лебега выпуклых функций. Свойство неотрицательности остатка выпуклой функции.
- •18. Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции.
- •20.Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •21.Метод исключения решения задачи на усл минимум. Пример.
- •23.Классич правило мн л в задаче опт-ции с огранич типа равенств. Необходим условия первого и второго порядка в задаче опт-ции типа равенств.
- •24.Достат условия экстремума в задаче опт-ции с ограничениями типа равенств.
- •25. Задача проектирования на выпуклое и замкнутое множество. Свойства проекции. Примеры.
- •27. Основные определения в задаче одномерной минимизации. Примеры.
- •Пример . Множ-во решений задачи min-ции f(X)
- •28.Метод деления отрезка пополам решения задачи одномерной минимизации.
- •29.Метод золотого сечения.
- •30.Метод ломаных. Обоснование и алгоритм. Пример.
- •31.Обоснование сходимости метода ломаных решения задачи одомерной минимизации
- •33. Алгоритм метода условного градиента
- •Теорема3
- •35. Сходимостсь метода скорейшого спуска
- •36. Постановка задачи вариационного исчисления. Пр.
- •Определим множество:
- •Замечание
- •37. Метод вариаций лагранжа Пусть в задаче , где и исследуется на минимум кривая , тогда все допустимые кривые X(t), из множества X можно представить в виде:
- •38. Уравнение Эйлера.
- •39. Случай интегрируемости ур-ния Эйлера. Пример.
- •40. Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •41. Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования.
- •42. Задача вариационного исчисления с движущимся по кривой коцом.
- •43. Примеры задач динамического программирования, их особенности.
- •44. Принципы динам програм и функцон ур-ния Беллмана.
- •45. Постановка задачи оптимального быстродействия.
- •46 Достат условия оптимальности для линейной задачи оптимального быстродействия (зоб).
- •47. Пример решения задач оптимального быстродействия.
24.Достат условия экстремума в задаче опт-ции с ограничениями типа равенств.
(1) (2)
Т1
Пусть в
задаче (1),(2)
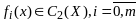 .Пусть в точке
вып необх усл оптимальности, а именно
.Пусть в точке
вып необх усл оптимальности, а именно
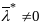 такой что
такой что
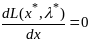 (3)и
допол-но квадратичн форма 2-ых производных
ф-ции Л
(3)и
допол-но квадратичн форма 2-ых производных
ф-ции Л
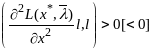 (4)
для всех векторов
(4)
для всех векторов
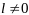 ,
удовл усл:
,
удовл усл:
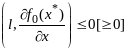 (5),
(6),
(5),
(6),
тогда точка явл строгим лок минимумом(лок максимумом) задачи (1),(2).
Зам.
В сформулир достат усл не требуется
обыкновенность планов
.
Док-во теоремы.
Док-во для задачи на минимум. Пусть усл
теоремы выполнено, но точка
не явл точкой строгого лок минимума,
тогда сущ посл-ть
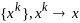 ,
такая что
,
такая что
 ,
,
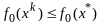 и
и
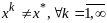 .
Точки
.
Точки
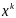 предс в виде:
предс в виде: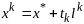 ,
,
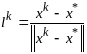 ,
,
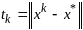 ,
,
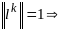 посл-ть векторов
посл-ть векторов
 явл ограниченной и в силу того, что
явл ограниченной и в силу того, что
 ,
то посл
стремится
,
то посл
стремится
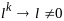 .Рассм
.Рассм
 ф-ции
ф-ции
 –диф-мы , поэтому
–диф-мы , поэтому
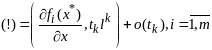 ,
для нулевой ф-ции
,
для нулевой ф-ции
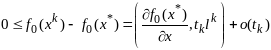 .Два
посл соотношения делим на
.Два
посл соотношения делим на
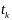 ,
устремляем
,
получаем:
;
,
устремляем
,
получаем:
;
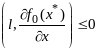 ,
т.е.
вектор
удовлетворяет усл (5),(6). Рассм ф-цию Л
,
т.е.
вектор
удовлетворяет усл (5),(6). Рассм ф-цию Л
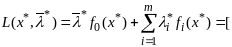 т.к.
х* удовлетв соотнош (6)
т.к.
х* удовлетв соотнош (6)

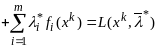 по предположению теоремы ф-ции
,
ф-ция Л тоже дважды диф-ма, т.е.
по предположению теоремы ф-ции
,
ф-ция Л тоже дважды диф-ма, т.е.
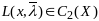 .
Рассмотрим разность
.
Рассмотрим разность
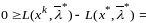
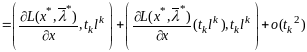 .
В силу усл (3) получаем
.
В силу усл (3) получаем
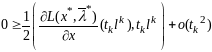 .
Последнее нер-во делим на
.
Последнее нер-во делим на
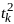 ,
,
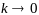 :
: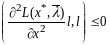 ,
т.е. нашли вектор
,
удовл усл (5),(6), на кот нарушается усл
(4). ?!
,
т.е. нашли вектор
,
удовл усл (5),(6), на кот нарушается усл
(4). ?!
25. Задача проектирования на выпуклое и замкнутое множество. Свойства проекции. Примеры.
Опр.
Расстояние от точки
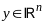 до
мн-ва
до
мн-ва
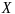 определ.
формулой
определ.
формулой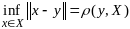 Функция
Функция
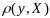 непр.
по y.
Опр.
Проекцией точки y
на мн-во X
наз. такая точка
непр.
по y.
Опр.
Проекцией точки y
на мн-во X
наз. такая точка
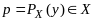 ,
для кот.
,
для кот.
 Задача нахождения точки p
наз задачей проектирования точки y
на мн-во X.
Если решение задачи проектирования
,
то норма
Задача нахождения точки p
наз задачей проектирования точки y
на мн-во X.
Если решение задачи проектирования
,
то норма
 Задачу
проектир. обычно заменяют равносильной
задачей
Задачу
проектир. обычно заменяют равносильной
задачей
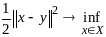 (1)
Задача (1) предст. собой задачу min-ции
квадратичной ф-ции.
(1)
Задача (1) предст. собой задачу min-ции
квадратичной ф-ции.
Утв1.
Если мн-во
явл.
Замкнутым и не пустым, то
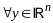
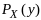 и
если
,
то
и
если
,
то

Док-во.
Пусть
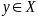 .
В противном сл.
.
В противном сл.
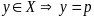 .
Рассм. произв. точку
.
Рассм. произв. точку
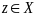 и
построим мн-во
и
построим мн-во
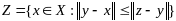 .
Мн-во
.
Мн-во
 не
явл. пустым, явл. замкнутым и огранич.
Поэтому по теор. Вейерштрасса
проекция точки y
на Z.
В силу постр. мн-ва Z:
не
явл. пустым, явл. замкнутым и огранич.
Поэтому по теор. Вейерштрасса
проекция точки y
на Z.
В силу постр. мн-ва Z:
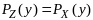 .
Пусть
.
Пусть
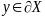
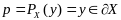 ,
,
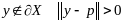 Предп. противное.
Предп. противное.
 .
Тогда
.
Тогда
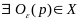 .
Рассм. отрезок, соед. точки y
и
p:
.
Рассм. отрезок, соед. точки y
и
p:
 .
Найдется такое
.
Найдется такое
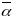 ,
что при
,
что при
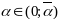
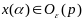 .
Рассм. расстояние
.
Рассм. расстояние
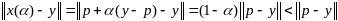
След-но,
p
не явл. проекцией.Утв2.
Если
непустое,
выпуклое и замкнутое, то
ед. проекция
Док-во.
Пусть
.
Тогда очевидно, что
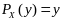 ,
поэтому явл. ед. Рассм., когда
,
поэтому явл. ед. Рассм., когда
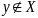 .
Предп., что
более одной проекции
.
Предп., что
более одной проекции
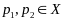 ,
,
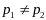 ,
,
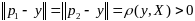 Вектора
Вектора
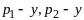 не
явл. коллинеарными. Действ-но, если
не
явл. коллинеарными. Действ-но, если
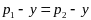 ,
то
,
то
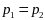 .
Если
.
Если
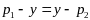 ,
то
,
то
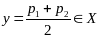 .
Это противоречит тому, что
.Рассм.
.
Это противоречит тому, что
.Рассм.
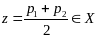
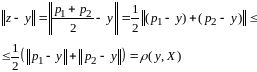
Нашли
точку
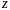 ,
такую
,
такую
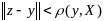 ,
что противор., что
,
что противор., что
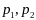 -проекции
Замеч.
Если мн-во не явл. выпуклым, то может
сущ. две проекции Рассм. примеры
нахождения проекций точек на мн-ва для
некот. конкр. мн-в
-проекции
Замеч.
Если мн-во не явл. выпуклым, то может
сущ. две проекции Рассм. примеры
нахождения проекций точек на мн-ва для
некот. конкр. мн-в
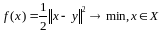
1)
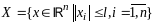
2)
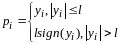
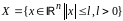
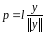
3)
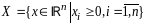
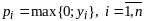
4)
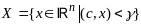 Т.к. проекция в любой точке, не принадл.
X,
будет принадл. границе мн-ва X,
то от данной задачи можно перейти к
задаче min-ции
функции f(x)
при ограничении
Т.к. проекция в любой точке, не принадл.
X,
будет принадл. границе мн-ва X,
то от данной задачи можно перейти к
задаче min-ции
функции f(x)
при ограничении
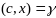 .
Т.к. c-ненулевой
вектор, сост. классич. ф-цию Лагранжа
.
Т.к. c-ненулевой
вектор, сост. классич. ф-цию Лагранжа
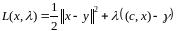 Система необходимых условий:
Система необходимых условий:
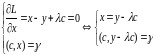
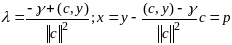
26. Необходимое условие минимума непрерывно дифференцируемой функции на выпуклом замкнутом множестве, сформулированное в терминах проекции точки на множество. Критерий решения задачи минимизации выпуклой непрерывно дифференцируемой функции на выпуклом замкнутом множестве.
Пусть (1).
Полагаем, что в задаче (1) функция -непрерывна дифференцируема, а мн-во Х- выпукло и замкнуто.
Теорема 1. Пусть т. -есть точка min в задаче (1). Тогда
Теорема 2. Пусть в задаче (1) функция выпукла, мн-во Х – выпукло, замкнуто, ограничено. Тогда для того, чтобы т. была т. min в задаче (1) необходимо и достаточно, чтобы т. была проекцией
Док-во: Из теоремы 1.
Ф-ия выпукла и -проекция;
Тогда можно сказать, что:
для выпуклой ф-ии .
Тогда можно сказать, что т. явл. точкой min ф-ии на мн-ве Х.
Замечание 1: Если функция непрерывна и диф-ма, а мн-во Х явл. выпуклым и замкнутым, тогда отображение, определяющее проекцию: , явл. конечным и однозначным.
Замечание 2: Необходимое условие min ф-ии на выпуклом, замкнутом мн-ве Х можно сформулировать в виде рав-ва:
