- •1. Понятие реш задач мат программирования. Постановка задач линейного программирования. Примеры. 1.
- •2 . Основные формы задача лп. Правило сведения злп к канон форме. Геометр интерпр злп. Понятие угловой точки мн-ва
- •3. Критерий угловой точки множества.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными злп.
- •7. Построение симплекс-таблицы. Достаточное условие оптимизации в задаче лп. Достаточное условие неразрешимости задачи лп.
- •8. Итерация симплекс-метода.
- •9. Обоснование конечности симплекс-алгоритма.
- •10. Обоснование непустоты множества планов в злп. Пример.
- •11.Нахождение базиса угловой точки. Пример. Св-во решений злп.
- •12. Свой-ва решений злп.
- •13. Постановка тз. Построение плана перевозок методом северо-западного угла.
- •14.Определение закрытой модели тз. Критерий существования решения тз.
- •Замечание Транспортная задача, для которой выполняется условие (1) называется закрытой, в противном случае – открытой.
- •15.Исследование множества клеток транспортной таблицы.
- •16.Достаточное условие минимальности стоимости перевозок
- •17. Определения выпуклого множества, выпуклой функции. Свойства выпуклых множеств. Сумма выпуклых функций. Свойство Лебега выпуклых функций. Свойство неотрицательности остатка выпуклой функции.
- •18. Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции.
- •20.Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •21.Метод исключения решения задачи на усл минимум. Пример.
- •23.Классич правило мн л в задаче опт-ции с огранич типа равенств. Необходим условия первого и второго порядка в задаче опт-ции типа равенств.
- •24.Достат условия экстремума в задаче опт-ции с ограничениями типа равенств.
- •25. Задача проектирования на выпуклое и замкнутое множество. Свойства проекции. Примеры.
- •27. Основные определения в задаче одномерной минимизации. Примеры.
- •Пример . Множ-во решений задачи min-ции f(X)
- •28.Метод деления отрезка пополам решения задачи одномерной минимизации.
- •29.Метод золотого сечения.
- •30.Метод ломаных. Обоснование и алгоритм. Пример.
- •31.Обоснование сходимости метода ломаных решения задачи одомерной минимизации
- •33. Алгоритм метода условного градиента
- •Теорема3
- •35. Сходимостсь метода скорейшого спуска
- •36. Постановка задачи вариационного исчисления. Пр.
- •Определим множество:
- •Замечание
- •37. Метод вариаций лагранжа Пусть в задаче , где и исследуется на минимум кривая , тогда все допустимые кривые X(t), из множества X можно представить в виде:
- •38. Уравнение Эйлера.
- •39. Случай интегрируемости ур-ния Эйлера. Пример.
- •40. Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •41. Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования.
- •42. Задача вариационного исчисления с движущимся по кривой коцом.
- •43. Примеры задач динамического программирования, их особенности.
- •44. Принципы динам програм и функцон ур-ния Беллмана.
- •45. Постановка задачи оптимального быстродействия.
- •46 Достат условия оптимальности для линейной задачи оптимального быстродействия (зоб).
- •47. Пример решения задач оптимального быстродействия.
33. Алгоритм метода условного градиента
Пусть
задано
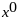
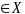 –некоторое начальное приближение.
Методом условного градиента найдена
т.
–некоторое начальное приближение.
Методом условного градиента найдена
т.
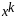 .Строим функцию:
.Строим функцию:
 и
решаем вспомогательную зад.
и
решаем вспомогательную зад.
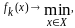 Пусть
Пусть –решение
вспомогательной задачи минимизации
–решение
вспомогательной задачи минимизации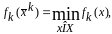 заметим, что
заметим, что
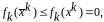
если
для некоторого k
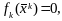 то т.
то т.
 удовлетворяет необходимому условию
минимума и процесс вычисления
заканчивается;
удовлетворяет необходимому условию
минимума и процесс вычисления
заканчивается;
если
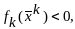 то строим отрезок
то строим отрезок
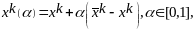 (5) и соединяем
точки
и
.
На отрезке (5)рассматриваем функцию
(5) и соединяем
точки
и
.
На отрезке (5)рассматриваем функцию
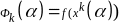 и решаем задачу одномерной минимизации
и решаем задачу одномерной минимизации
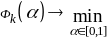 .
Обозначим через
.
Обозначим через
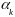 –решение последней зад. минимизации
т.е
–решение последней зад. минимизации
т.е
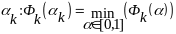 ,
тогда следующее приближение
,
тогда следующее приближение
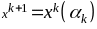 .
.
Замечание:
Метод условного градиента является эффективным в том случае, когда вспомогательная зад.
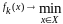 допускает простое решение;
допускает простое решение;На каждом шаге метода условного градиента решается зад. одномерной минимизации
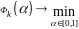 .
Для некоторых классов задач, решение
этой задачи удается найти в явном виде,
например, в случае квадратичной целевой
функции. Для некоторых классов задач
для решения задачи
.
Для некоторых классов задач, решение
этой задачи удается найти в явном виде,
например, в случае квадратичной целевой
функции. Для некоторых классов задач
для решения задачи
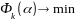 применяют численные методы одномерной
минимизации. На практике часто пользуются
следующим алгоритмом:
применяют численные методы одномерной
минимизации. На практике часто пользуются
следующим алгоритмом:
Задают некоторое значение и проверяют условие
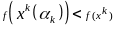 (6)
(6)В случае выполнения (6),
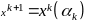 ;
иначе
дробят
;
иначе
дробят
В качестве критериев окончания счета используют выполнение неравенств
 или
или
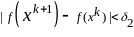 ,
где
,
где
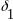 и
и
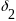 согласованные числа, характеризующие
точность вычисления.
согласованные числа, характеризующие
точность вычисления.
Теорема3
Если
функция f(x)
в зад.(1) непрерывно дифференцируема
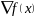 ,
удовлетворяет векторному условию
Липшица, множество Х
- выпукло,
замкнуто и ограничено, то при любом
начальном приближении
,
удовлетворяет векторному условию
Липшица, множество Х
- выпукло,
замкнуто и ограничено, то при любом
начальном приближении
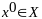 процесс
метода условного градиента является
релаксационным и сходится к непустому
множеству
процесс
метода условного градиента является
релаксационным и сходится к непустому
множеству
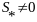 стационарных точек. Если дополнительно
f(x)
выпукло, то построенная последовательность
является минимизирующей и сходится к
непустому множеству
стационарных точек. Если дополнительно
f(x)
выпукло, то построенная последовательность
является минимизирующей и сходится к
непустому множеству
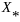 решений задачи.
решений задачи.
34. Алгоритм метода покоординатного спуска.
Рассмотрим
задачу
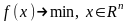 .
Пусть выбрано некоторое
начальное приближение. И мтодом
покоординатного спуска было получено
приближение
.
Пусть выбрано некоторое
начальное приближение. И мтодом
покоординатного спуска было получено
приближение
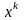 .
Ч/з
.
Ч/з
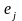 ,
,
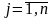 ,
обозначим координатные вектора
,
обозначим координатные вектора
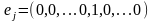 (1
на j-ом
месте). Положим
(1
на j-ом
месте). Положим
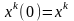 и для
и для
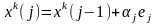 ,
где
,
где
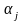 определяется из условия
определяется из условия
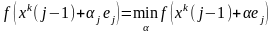 .
И следующее приближение
.
И следующее приближение
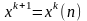 ,
если для некоторого k
,
если для некоторого k
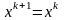 ,
то процесс вычисления заканчивают, А т
считают приближением к точке минимума.
,
то процесс вычисления заканчивают, А т
считают приближением к точке минимума.

Данный метод хорошо подходит для задач с параллепипедными ограничениями,
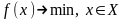 ,
,
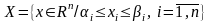 .
В этом случае при решении вспомагательной
задачи минимизации
.
В этом случае при решении вспомагательной
задачи минимизации
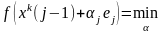 ,
,
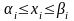 .
.
35. Сходимостсь метода скорейшого спуска
Т.1:Пусть
в задаче (1)
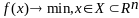 ,
целевая функция J(x)
непрер. диффер.,огранич. с низу и её
градиент удовл.вект.усл.Липшица
,
целевая функция J(x)
непрер. диффер.,огранич. с низу и её
градиент удовл.вект.усл.Липшица 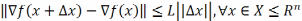
Тогда
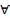 нач.
приближ.
нач.
приближ. 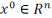 итерационный
процесс метода скор. спуска
явл.релаксацирнным, т.е.
итерационный
процесс метода скор. спуска
явл.релаксацирнным, т.е.
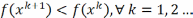 и стремится к выполнению необх-го усл.
минимума, т.е.
и стремится к выполнению необх-го усл.
минимума, т.е. 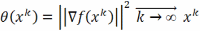
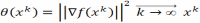 .
.
Если
доп.множество 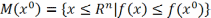 огран.,
то послед-сть
огран.,
то послед-сть 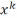 построенная методом скор. спуска сх-ся
к непустому мн-ву
построенная методом скор. спуска сх-ся
к непустому мн-ву  стац. точек задачи (1)
стац. точек задачи (1) 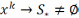 .
Если кроме этого функция
.
Если кроме этого функция  в задаче (1) явл.выпуклой,то последовательность
явл.минимизирующей
и сх-ся к непустому мн-ву решений з. (1)
в задаче (1) явл.выпуклой,то последовательность
явл.минимизирующей
и сх-ся к непустому мн-ву решений з. (1)
 Док-во:
1) Если
k,
Док-во:
1) Если
k,
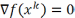 ,
то процесс метода скорейшего спуска
заканчивается, след.приближение
,
то процесс метода скорейшего спуска
заканчивается, след.приближение 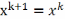 .
Точка
.
Точка 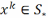
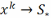 и если
выпукло, то
и если
выпукло, то 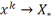
 .
Будем считать далее, что
.
Будем считать далее, что 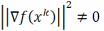
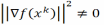 .
тогда положим:
.
тогда положим:
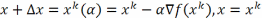
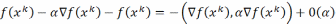
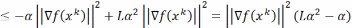
Точка
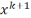 в методе скор. спуска определяется из
условия, что
в методе скор. спуска определяется из
условия, что 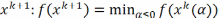 .
Тогда имеем
.
Тогда имеем
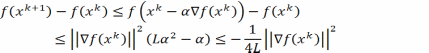
 (3)
(3)
Нер-во
(3) обосновывает релаксационность
процесса. Т.о. послед-сть 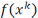 монотонно убывает. Ф-ия
ограничена
снизу, поэтому посл-ть
монотонно убывает. Ф-ия
ограничена
снизу, поэтому посл-ть 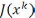 как монотонно убывающая и огранич. снизу
имеет предел
как монотонно убывающая и огранич. снизу
имеет предел 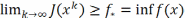
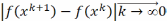 .
Перейдя в нер-ве (3)к пределу
.
Перейдя в нер-ве (3)к пределу 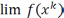 получаем
получаем 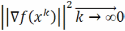
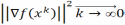 .
2) мн-во М(х0)
явл. огранич. В силу построения М(х0)-замкн.
мн-во. Ф-ия f(x)
непрер., поэтому по т.Вейштрасса реш.
зад. Миним-ии ф-ии f(x)
по мн-ву M(x0)
сущ. Поэтому мн-во Х*
решений
зад.(1) не явл. пустым и Х*
явл. подмн-ом
M(x0).
Т.о. посл. хк
явл. оранич.
Из огранич. послед-сти можно выделить
сходящуюся.Пусть подпосл-ть
.
2) мн-во М(х0)
явл. огранич. В силу построения М(х0)-замкн.
мн-во. Ф-ия f(x)
непрер., поэтому по т.Вейштрасса реш.
зад. Миним-ии ф-ии f(x)
по мн-ву M(x0)
сущ. Поэтому мн-во Х*
решений
зад.(1) не явл. пустым и Х*
явл. подмн-ом
M(x0).
Т.о. посл. хк
явл. оранич.
Из огранич. послед-сти можно выделить
сходящуюся.Пусть подпосл-ть 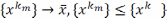 .
. Поэтому
Поэтому
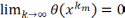 но т.к.
но т.к. 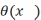 -ф-ия
непр., то этот предел равен ф-ии
-ф-ия
непр., то этот предел равен ф-ии 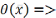 любая
предельная т. посл.
любая
предельная т. посл.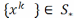 .
А т.о. хотябы одна предельная т.сущ. то
мн-во
.
А т.о. хотябы одна предельная т.сущ. то
мн-во 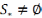 .Докажем
теперь, что
.Докажем
теперь, что 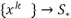 .
Ф-ия расстояния от т. до мн.
.
Ф-ия расстояния от т. до мн. 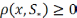 ,
поэтому
,
поэтому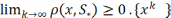
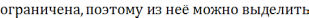
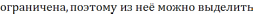 сходящуюся. Пусть подпосл.
сходящуюся. Пусть подпосл.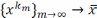 ;
; .Ф-ия
расстояния явл. непрер. ф-ей точки,
поэтому
.Ф-ия
расстояния явл. непрер. ф-ей точки,
поэтому 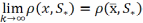 .
Но по первой части док-ва, каждая
предельная точка посл.{xk}
.
Но по первой части док-ва, каждая
предельная точка посл.{xk}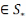 , то
, то 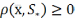 Последне ра-во справедливо для любой
сходящейся посл-ти {xk}:
Последне ра-во справедливо для любой
сходящейся посл-ти {xk}: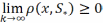 3)Пусть ф-ия f(x)-выпукла
, тогда на м-ве М(х0)
зад.(1) имеет решение т.е. сущ.т.
3)Пусть ф-ия f(x)-выпукла
, тогда на м-ве М(х0)
зад.(1) имеет решение т.е. сущ.т. 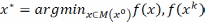 Отсюда
Отсюда 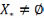 .
По cв-ву
неотр-ти остатка выпуклой ф-ии имеем
.
По cв-ву
неотр-ти остатка выпуклой ф-ии имеем
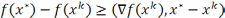
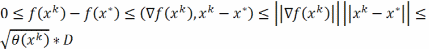
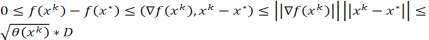 где
D<
где
D<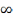 в силу огран-ти М(х0).
Переходя к пределу в последнем нер-ве
получаем
в силу огран-ти М(х0).
Переходя к пределу в последнем нер-ве
получаем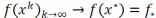 ,
т.е. посл.
явл. минимизир. Аналогично 2-ой части
док-ва доказыв., что
,
т.е. посл.
явл. минимизир. Аналогично 2-ой части
док-ва доказыв., что