
- •1. Понятие реш задач мат программирования. Постановка задач линейного программирования. Примеры. 1.
- •2 . Основные формы задача лп. Правило сведения злп к канон форме. Геометр интерпр злп. Понятие угловой точки мн-ва
- •3. Критерий угловой точки множества.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными злп.
- •7. Построение симплекс-таблицы. Достаточное условие оптимизации в задаче лп. Достаточное условие неразрешимости задачи лп.
- •8. Итерация симплекс-метода.
- •9. Обоснование конечности симплекс-алгоритма.
- •10. Обоснование непустоты множества планов в злп. Пример.
- •11.Нахождение базиса угловой точки. Пример. Св-во решений злп.
- •12. Свой-ва решений злп.
- •13. Постановка тз. Построение плана перевозок методом северо-западного угла.
- •14.Определение закрытой модели тз. Критерий существования решения тз.
- •Замечание Транспортная задача, для которой выполняется условие (1) называется закрытой, в противном случае – открытой.
- •15.Исследование множества клеток транспортной таблицы.
- •16.Достаточное условие минимальности стоимости перевозок
- •17. Определения выпуклого множества, выпуклой функции. Свойства выпуклых множеств. Сумма выпуклых функций. Свойство Лебега выпуклых функций. Свойство неотрицательности остатка выпуклой функции.
- •18. Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции.
- •20.Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •21.Метод исключения решения задачи на усл минимум. Пример.
- •23.Классич правило мн л в задаче опт-ции с огранич типа равенств. Необходим условия первого и второго порядка в задаче опт-ции типа равенств.
- •24.Достат условия экстремума в задаче опт-ции с ограничениями типа равенств.
- •25. Задача проектирования на выпуклое и замкнутое множество. Свойства проекции. Примеры.
- •27. Основные определения в задаче одномерной минимизации. Примеры.
- •Пример . Множ-во решений задачи min-ции f(X)
- •28.Метод деления отрезка пополам решения задачи одномерной минимизации.
- •29.Метод золотого сечения.
- •30.Метод ломаных. Обоснование и алгоритм. Пример.
- •31.Обоснование сходимости метода ломаных решения задачи одомерной минимизации
- •33. Алгоритм метода условного градиента
- •Теорема3
- •35. Сходимостсь метода скорейшого спуска
- •36. Постановка задачи вариационного исчисления. Пр.
- •Определим множество:
- •Замечание
- •37. Метод вариаций лагранжа Пусть в задаче , где и исследуется на минимум кривая , тогда все допустимые кривые X(t), из множества X можно представить в виде:
- •38. Уравнение Эйлера.
- •39. Случай интегрируемости ур-ния Эйлера. Пример.
- •40. Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •41. Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования.
- •42. Задача вариационного исчисления с движущимся по кривой коцом.
- •43. Примеры задач динамического программирования, их особенности.
- •44. Принципы динам програм и функцон ур-ния Беллмана.
- •45. Постановка задачи оптимального быстродействия.
- •46 Достат условия оптимальности для линейной задачи оптимального быстродействия (зоб).
- •47. Пример решения задач оптимального быстродействия.
18. Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции.
(1) (2)
Т.(о точках минимума выпуклой ф-ии): Пусть в задаче (1)-(2) ф-ия выпукла, определена на выпуклом мн-ве Х, тогда:
1) каждая точка ее локального минимума (если такая сущ-ет), явл-ся точкой глобального минимума;
2)
Мн-во
 решений задачи (1), (2) явл-ся выпуклым;
решений задачи (1), (2) явл-ся выпуклым;
3) если ф-ия строго выпукла, то она может достичь своего min не более чем в одной точке.
Док-во:
1) Пусть
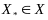 есть точка глобальн min
ф-ии
,
т.е.
есть точка глобальн min
ф-ии
,
т.е.
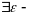 окрестность
этой точки
окрестность
этой точки
 ,
так что
,
так что
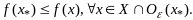 Пусть
точка
Пусть
точка
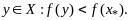 Соединим эти точки отрезком
Соединим эти точки отрезком
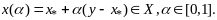
Т.к.
мн-во Х явл-ся выпуклым , то при всех
 :
:

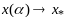 при
при
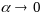 ,
след-но найдется такое значение
,
след-но найдется такое значение
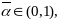 что
что
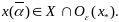 Поэтому
Поэтому
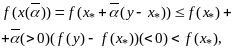
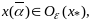 что противоречит
тому, что т.
что противоречит
тому, что т.
 явл-ся точкой локальн min.
явл-ся точкой локальн min.
2)
Мн-во
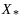 -
мн-во решений задачи
-
мн-во решений задачи
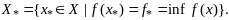 Пусть мн-во
Пусть мн-во
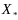 состоит более чем из одной точки. Возьмем
состоит более чем из одной точки. Возьмем
 Рассмотрим
Рассмотрим
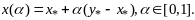 Т.к. ф-ия
-
выпукла, то
Т.к. ф-ия
-
выпукла, то
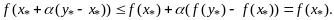
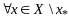 выполняется нер-во
выполняется нер-во
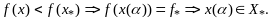
3)
Предположим сущ-ет точка
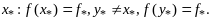 Соединим точки
и
Соединим точки
и
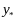 отрезком:
отрезком:
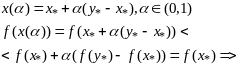
мы
нашли точку
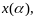 в которой
в которой
 что противоречит тому, что
явл-ся точкой локального min.
Теорема доказана.
что противоречит тому, что
явл-ся точкой локального min.
Теорема доказана.
Т 2 (о стационарной точке выпуклой ф-ции): Каждая стационарная точка выпуклой функции , определенная на выпуклом множестве Х, является ее точкой минимума.
Док-во:
Пусть
стационарная точка ф-ции
,
т.е.
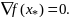 Рассмотрим произвольную точку
Рассмотрим произвольную точку
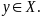 Для точек
Для точек
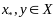 в силу выпуклости ф-ции
выполняется:
в силу выпуклости ф-ции
выполняется:
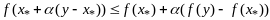 (3)
(3)
Т.к. ф-ция дифференцируема, то приращение (из (3))=>
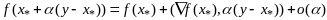 .
.
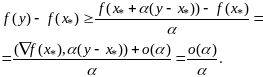
По
свойству неотрицательности остатка

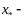 точка
минимума. Теорема доказана.
точка
минимума. Теорема доказана.
19. Необходимое условие минимума непрерывно дифференцируемой функции на выпуклом замкнутом множестве, сформулированное в терминах проекции точки на множество. Критерий решения задачи минимизации выпуклой непрерывно дифференцируемой функции на выпуклом замкнутом множестве.
Пусть
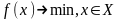 (1).
(1).
Полагаем,
что в задаче (1) функция
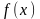 -непрерывна
дифференцируема, а мн-во Х- выпукло и
замкнуто.
-непрерывна
дифференцируема, а мн-во Х- выпукло и
замкнуто.
Теорема
1. Пусть
т.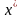 -есть
точка min
в задаче (1). Тогда
-есть
точка min
в задаче (1). Тогда
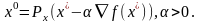
Теорема
2. Пусть
в задаче (1) функция
выпукла, мн-во Х – выпукло, замкнуто,
ограничено. Тогда для того, чтобы т.
была т. min
в задаче (1)
необходимо и достаточно, чтобы т.
была проекцией
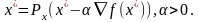
Док-во:
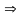 Из
теоремы 1.
Из
теоремы 1.
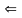 Ф-ия
выпукла и
-проекция;
Ф-ия
выпукла и
-проекция;
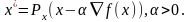
Тогда можно сказать, что:
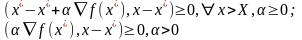
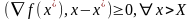 для
выпуклой ф-ии
.
для
выпуклой ф-ии
.
Тогда можно сказать, что т. явл. точкой min ф-ии на мн-ве Х.
Замечание
1: Если
функция
непрерывна
и диф-ма, а мн-во Х явл. выпуклым и
замкнутым, тогда отображение, определяющее
проекцию:
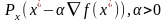 ,
явл. конечным и однозначным.
,
явл. конечным и однозначным.
Замечание 2: Необходимое условие min ф-ии на выпуклом, замкнутом мн-ве Х можно сформулировать в виде рав-ва:
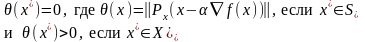
20.Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
Под кл. методом подразум. подход к поиску экстремумов ф-ции многих переменных, осн. на дифференц. исчисл.
Т1
Вейерштрасса о
достижении непрер. ф. точной верхней
(точной нижней) грани на огранич. замкнут.
мн-ве. Пусть в задаче
 (1),
мн-во Х не пусто, ограничено, замкнуть;
f(x)
определена, принимает конечн. значения
и непрерывна на мн-ве Х, тогда решение
зад. (1) сущ, т.е.
(1),
мн-во Х не пусто, ограничено, замкнуть;
f(x)
определена, принимает конечн. значения
и непрерывна на мн-ве Х, тогда решение
зад. (1) сущ, т.е.
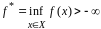 ,
,
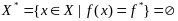 ,
мн-во Х* - мн-во решений.
,
мн-во Х* - мн-во решений.
Сл
из Т1 Пусть
мн-во X
в задаче (1) замкнуть, f(x)
непреп. на X.
Пусть сущ.
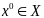 ,
такое, что мн-во
,
такое, что мн-во
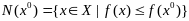 ограничено, тогда ф.f(x)
достигает своей нижней грани на мн-ве
X.
ограничено, тогда ф.f(x)
достигает своей нижней грани на мн-ве
X.
Зам1.
Т. Вейер..
представл. собой достат. условие сущ.
решения в задаче (1). Зам2.
В любой точке
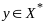 вып.
нер-во
вып.
нер-во
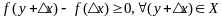 .(2)
Обратно, если
.(2)
Обратно, если
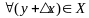 вып. нер-во (2), то точка у явл. решением
задачи (1).
вып. нер-во (2), то точка у явл. решением
задачи (1).
Т2
Пусть
диф-ма в точке
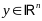 и точка у явл точкой лок минимума ф-ции
,
тогда
и точка у явл точкой лок минимума ф-ции
,
тогда
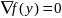 (градиен). Док-во.
Возьмем
произв точку
(градиен). Док-во.
Возьмем
произв точку
 и
построим точки
и
построим точки
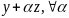 .
Рассмотрим приращение
.
Рассмотрим приращение
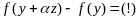 ,
т.к. ф f(x)
диф-ма в точке у, то
,
т.к. ф f(x)
диф-ма в точке у, то
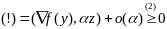 .
Возьмем
.
Возьмем
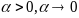 (разделим
на
и
(разделим
на
и
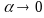 ):
):
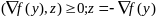 ,
,
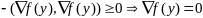 .
.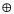
Зам
3. В точке, в
кот градиент целевой ф-ции =0, наз стац-ным.
Зам 4 Поиск
точек экстремума можно начинать с поиска
стац. точек, т.е. с решения системы n
уравнений с n
неизвестными
.
Т 3 Пусть
ф-ция f(x)
дважды диф-ма в точке у, если у есть точка
локальн минимума задачи (1),то матрица
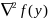 (наз матрицей Гессе) вторых частных
производных целевой ф-ции неотр опред
,т.е.
(наз матрицей Гессе) вторых частных
производных целевой ф-ции неотр опред
,т.е.
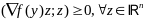 .
Док-во В
силу того, что точка у явл точкой лок
минимума задачи (1)
,
тогда
.
Док-во В
силу того, что точка у явл точкой лок
минимума задачи (1)
,
тогда
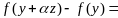
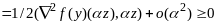 .
Разделим на
,
.
Разделим на
,
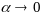 :
:
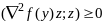 .
Зам 6 Если
точка у явл точкой лок максимума, то для
любого
вып-ся
.
Зам 6 Если
точка у явл точкой лок максимума, то для
любого
вып-ся
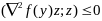 .
Т4 Достат усл оптимальности. Пусть
ф-ция f(x)
дважды диф-ма в точке
,
,
.
Т4 Достат усл оптимальности. Пусть
ф-ция f(x)
дважды диф-ма в точке
,
,
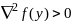 ,
т.е.
,
т.е.
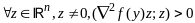 ,
тогда точка у явл точкой лок минимума
задачи (1). Док-во
от
противного.Пусть точка у , удовл усл
теоремы, не явл точкой лок минимума
задачи (1) тогда сущ посл-сть
,
тогда точка у явл точкой лок минимума
задачи (1). Док-во
от
противного.Пусть точка у , удовл усл
теоремы, не явл точкой лок минимума
задачи (1) тогда сущ посл-сть
 такая что
такая что
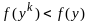 .
Представим
.
Представим
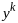 в виде:
в виде:
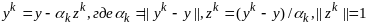 поэтому
последовательность
поэтому
последовательность
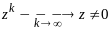 .
Рассм приращение
.
Рассм приращение
 Посл нер-во разделим на
Посл нер-во разделим на
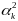 и
устремим
и
устремим
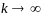 ,
тем самым
,
тем самым
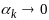 :
,
:
,
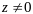 ?!
Квадрат. форма
?!
Квадрат. форма
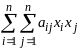 =(1),
если
=(1),
если
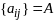 ,
то
,
то
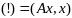 .
Знакоопредел квадр формы пред с пом
критерия Сильвестра.
.
Знакоопредел квадр формы пред с пом
критерия Сильвестра.
Пример.
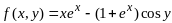 ;
;
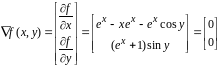 ;
;
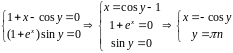 ;
;
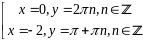 ;
;
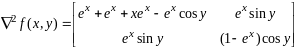
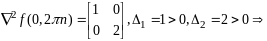 матрица
положит опред, необх усл 2-го порядка
вып, дост усл вып, следовательно точки
(0,2Пn)
явл точками минимума.
матрица
положит опред, необх усл 2-го порядка
вып, дост усл вып, следовательно точки
(0,2Пn)
явл точками минимума.
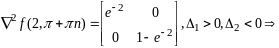 квадр
форма знаконеопред, необх усл 2-го порядка
не выр, следовательно, точки(2,П+Пn)
не явл точками экстемума Зам
7 Т2-Т4 работают
когда мн-во
квадр
форма знаконеопред, необх усл 2-го порядка
не выр, следовательно, точки(2,П+Пn)
не явл точками экстемума Зам
7 Т2-Т4 работают
когда мн-во
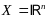 совпадает со всем пространством, в этом
случае задача (1) наз задачей безусловной
оптимизации, если мн-во
совпадает со всем пространством, в этом
случае задача (1) наз задачей безусловной
оптимизации, если мн-во
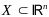 чвл
строгим подмн-вом пр-ва
чвл
строгим подмн-вом пр-ва
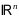 ,
то задача (1) наз задачей усл оптимизации.
Для задачи усл опт-ции Т2-Т4 справедливы,
если
,
то задача (1) наз задачей усл оптимизации.
Для задачи усл опт-ции Т2-Т4 справедливы,
если
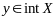 (принадлежит
внутренности мн-ва. Х) Однако это не
всегда так.Зам
8 Если в
задаче (1) ф-ция
(принадлежит
внутренности мн-ва. Х) Однако это не
всегда так.Зам
8 Если в
задаче (1) ф-ция
 ,
то Т2-Т4 легко обобщаются:
,
то Т2-Т4 легко обобщаются:
1
если у –
точка минимума ф-ции f(x)
на отр. [a,b]: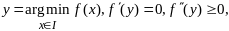 Если
Если
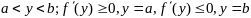 при усл сущ-ния производных
при усл сущ-ния производных
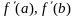 поним как односторонние производные.
2 если
поним как односторонние производные.
2 если
 ,
то точка у явл точкой лок минимума ф-ции
f(x)на
отрезке
,
то точка у явл точкой лок минимума ф-ции
f(x)на
отрезке
 .
.
