
- •1. Понятие реш задач мат программирования. Постановка задач линейного программирования. Примеры. 1.
- •2 . Основные формы задача лп. Правило сведения злп к канон форме. Геометр интерпр злп. Понятие угловой точки мн-ва
- •3. Критерий угловой точки множества.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными злп.
- •7. Построение симплекс-таблицы. Достаточное условие оптимизации в задаче лп. Достаточное условие неразрешимости задачи лп.
- •8. Итерация симплекс-метода.
- •9. Обоснование конечности симплекс-алгоритма.
- •10. Обоснование непустоты множества планов в злп. Пример.
- •11.Нахождение базиса угловой точки. Пример. Св-во решений злп.
- •12. Свой-ва решений злп.
- •13. Постановка тз. Построение плана перевозок методом северо-западного угла.
- •14.Определение закрытой модели тз. Критерий существования решения тз.
- •Замечание Транспортная задача, для которой выполняется условие (1) называется закрытой, в противном случае – открытой.
- •15.Исследование множества клеток транспортной таблицы.
- •16.Достаточное условие минимальности стоимости перевозок
- •17. Определения выпуклого множества, выпуклой функции. Свойства выпуклых множеств. Сумма выпуклых функций. Свойство Лебега выпуклых функций. Свойство неотрицательности остатка выпуклой функции.
- •18. Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции.
- •20.Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •21.Метод исключения решения задачи на усл минимум. Пример.
- •23.Классич правило мн л в задаче опт-ции с огранич типа равенств. Необходим условия первого и второго порядка в задаче опт-ции типа равенств.
- •24.Достат условия экстремума в задаче опт-ции с ограничениями типа равенств.
- •25. Задача проектирования на выпуклое и замкнутое множество. Свойства проекции. Примеры.
- •27. Основные определения в задаче одномерной минимизации. Примеры.
- •Пример . Множ-во решений задачи min-ции f(X)
- •28.Метод деления отрезка пополам решения задачи одномерной минимизации.
- •29.Метод золотого сечения.
- •30.Метод ломаных. Обоснование и алгоритм. Пример.
- •31.Обоснование сходимости метода ломаных решения задачи одомерной минимизации
- •33. Алгоритм метода условного градиента
- •Теорема3
- •35. Сходимостсь метода скорейшого спуска
- •36. Постановка задачи вариационного исчисления. Пр.
- •Определим множество:
- •Замечание
- •37. Метод вариаций лагранжа Пусть в задаче , где и исследуется на минимум кривая , тогда все допустимые кривые X(t), из множества X можно представить в виде:
- •38. Уравнение Эйлера.
- •39. Случай интегрируемости ур-ния Эйлера. Пример.
- •40. Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •41. Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования.
- •42. Задача вариационного исчисления с движущимся по кривой коцом.
- •43. Примеры задач динамического программирования, их особенности.
- •44. Принципы динам програм и функцон ур-ния Беллмана.
- •45. Постановка задачи оптимального быстродействия.
- •46 Достат условия оптимальности для линейной задачи оптимального быстродействия (зоб).
- •47. Пример решения задач оптимального быстродействия.
36. Постановка задачи вариационного исчисления. Пр.
Говорят,
что на некотором классе функций задан
функционал, если каждой функции x=x(t)
из этого класса, поставлено в соответствие
число
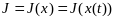 .
Если кажд. функцию x(t)
рассматривать, как элемент некоторого
пространства L,
например пространство непрерывных
функций, непрерывно дифференцируемых
функций, то
.
Если кажд. функцию x(t)
рассматривать, как элемент некоторого
пространства L,
например пространство непрерывных
функций, непрерывно дифференцируемых
функций, то
 ,где
,где

В
пространстве L
можно рассматривать некоторые множества
X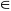 L,
например множество
L,
например множество
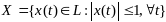
Тогда можно рассматривать задачу оптимизации в функциональном пространстве, кот. формально может быть записаннa в той же форме, что и задача мат. прогр:
Найти
такое
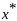 ,
что
,
что
 .
(1)
.
(1)
Задача
(1) понимается в глобальном смысле, если
необходимо найти функцию, доставляющую
линейному функционалу J(x)
по всем x
X
и понимаемом
в лок смысле, если,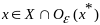 ,
где
,
где
Сформулируем зад. вариационного исчисления:
Пусть
на отрезке T=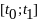 определена непрерывно дифференцируемая
функция x(t),
принимающая на концах отрезка заданные
значения:
определена непрерывно дифференцируемая
функция x(t),
принимающая на концах отрезка заданные
значения: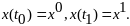
Определим множество:
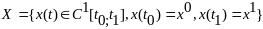 (2)
(2)
И на этом множестве определена функция:
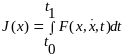 (3)
(3)
Где
функция
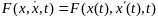 определена и непрерывна по всем своим
аргументам вместе с частными производными
по x,
определена и непрерывна по всем своим
аргументам вместе с частными производными
по x,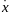 ,t
до 2-го
порядка. Требуется найти функцию
,t
до 2-го
порядка. Требуется найти функцию
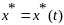 ,
такую что
,
такую что
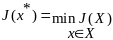 (4)
(4)
Функции
из множества (2) называются допустимыми,
а функция
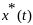 называется минималью.
называется минималью.
Зад.
(2)-(4) обычно понимается в локальном
смысле, т.е. минимум ищется по функциям
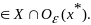
если
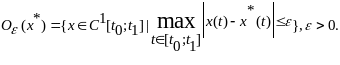
то говорят о сильном локальном минимуме
если
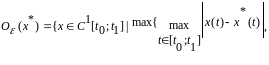

то говорят о слабом локальном минимуме
Замечание
Е сли
на некоторой кривой
сли
на некоторой кривой достигается
сильный локальный минимум, то на ней
достигается и слабый локальный минимум,
но не наоборот. Поэтому необходимые
условия слабого локального минимума
будут являться и необходимыми условиями
сильного локального минимума, но не
наоборот.
достигается
сильный локальный минимум, то на ней
достигается и слабый локальный минимум,
но не наоборот. Поэтому необходимые
условия слабого локального минимума
будут являться и необходимыми условиями
сильного локального минимума, но не
наоборот.
Пример: (зад. о бахистохроне – кривая наискорейшего времени )
На
плоскости заданы 2-е точки А и B.
Введем декартовую систему координат:
т. А попадает в начало координат, а т.B
имеет координаты
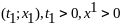 .Из А в B
скатывается тяжелая материальная точка.
.Из А в B
скатывается тяжелая материальная точка.
Найти кривую x(t) по которой перемещение из А в B произойдет за минимальное время.
Начальная
скорость
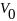 .
Точка скатывается под воздействием
силы тяжести; сопротивление не учитывается,
поэтому скорость точки зависит только
от положения точки и не зависит от формы
кривой.
.
Точка скатывается под воздействием
силы тяжести; сопротивление не учитывается,
поэтому скорость точки зависит только
от положения точки и не зависит от формы
кривой.
По
закону Галия:
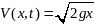 ,
где g-
ускорение свободного падения. С другой
стороны, скорость в каждый момент времени
вычисляется, как отношение
,
где g-
ускорение свободного падения. С другой
стороны, скорость в каждый момент времени
вычисляется, как отношение
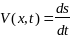 ,
где ds-
дифференциал дуги, которая будет
пройденна точкой за время dt.
,
где ds-
дифференциал дуги, которая будет
пройденна точкой за время dt.
Известно,
что
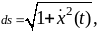
Т.о.
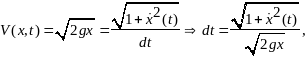
Тогда
время, которое необходимо точке для
перехода из А в B
определяется как
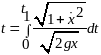
Т.о.
получаем следующую задачу вариационного
исчисления:
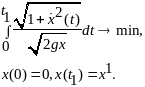
37. Метод вариаций лагранжа Пусть в задаче , где и исследуется на минимум кривая , тогда все допустимые кривые X(t), из множества X можно представить в виде:

Тогда рассмотрим приращение функционала:
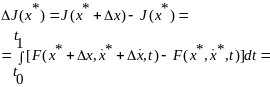
=/ в силу дифференцируемости функции F/=
=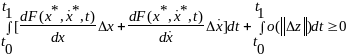 (т.к
(т.к минимально),
где
минимально),
где
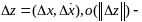 бесконечно
малая велич.
бесконечно
малая велич.
В
таком разложении приращения функционала,
кривые
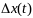 имеют произвольную природу, что влечет
за собой сложность исследования.
Представим кривые
в виде однопараметрического семейства
функций:
имеют произвольную природу, что влечет
за собой сложность исследования.
Представим кривые
в виде однопараметрического семейства
функций:
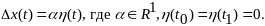
Для таких приращений функций рассмотрим приращение функционала:
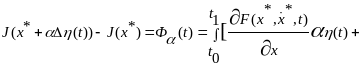
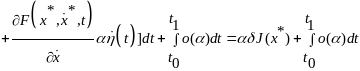
где
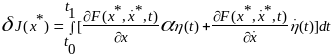
наз. первой вариацией функционала. Т.к
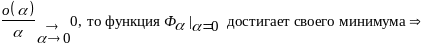
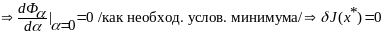
( на кривой подозрительной на минимум)
Замечание:
Необходимое
условие оптимальности
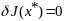 в силу произвольности функций
в силу произвольности функций
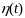 является неудобным для использования.
является неудобным для использования.
