
- •1.Понятие решения задачи мат. Программиров.
- •2. Основн. Формы злп. Правила сведения злп к канон.Форме. Геометр.Интерпретация злп. Понятие угловой точки мн-ва.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными задачи лп
- •6. Формула приращения целевой функции злп.
- •7. Достаточное условие оптимальности в злп. Достаточное условие неразрешимости злп
- •8. Итерация симплекс–метода
- •11. Нахождение базиса угловой точки. Пример
- •12. Постановка тз. Построение нач. Плана перевозок методом северо-западного угла, методом мин. Элемента.
- •13. Определение закрытой модели тз. Критерий существования решения тз.
- •14. Исследование мн-ва клеток транспортной таблицы
- •15. Достаточное условие минимальности стоимости перевозок
- •16. Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •17. Метод исключения решения задачи на условный минимум. Пример.
- •18. Обобщенное правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств.
- •19. Классическое правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств. Необходимые условия второго порядка в задаче оптимизации типа равенств.
- •20. Достаточные условия экстремума в задаче оптимизации с ограничениями типа равенств
- •21.Опр-ия выпуклого мн-ва, выпуклой функции. Св-ва выпуклых множеств. Сумма выпуклых функций. Св-во неотрицательности остатка выпуклой функции
- •22.Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции
- •26.Теорема о седловой точке функции Лагранжа (достаточные условия оптимальности).
- •27. Критерий существования седловой точки функции Лагранжа для задачи выпуклого программирования.
- •28.Определение двойственной задачи к задаче математического программирования.
- •29. Связь между двойственной и прямой задачами математического программирования.
- •30.Пример решения задачи оптимизации с помощью теории двойственности
- •31.Основные определения в задаче одномерной минимизации. Примеры.
- •33. Метод золотого сечения решения задачи одномерной минимизации.
- •34. Обоснование метода ломаных решения задачи одномерной минимизации.
- •35. Алгоритм и условия сходимости метода ломаных решения задачи одномерной минимизации. Пример. Описание метода ломаных
- •36.Алгоритм метода скорейшего спуска решения змм.
- •37.Алгоритмы метода условного градиента и метода проекции градиента решения задачи многомерной условной минимизации.
- •38.Алгоритм метода покоординатного спуска решения задачи многомерной минимизации. Геометрическая иллюстрация.
- •39.Сходимость метода скорейшего спуска.
- •41. Метод вариаций Лагранжа
- •42. Уравнение Эйлера
- •43. Случаи интегрируемости ур-ния Эйлера. Примеры.
- •44.Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •45.Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования
- •46. Задача вариационного исчисления с движущимся по кривой концом.
- •47. Примеры задач динамического программирования, их особенности
- •48.Принципы динамического программирования и функциональные уравнения Беллмана.
1.Понятие решения задачи мат. Программиров.
Пусть на некотором
мн-ве
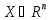 задана
скалярная ф-яf(x),
точки
задана
скалярная ф-яf(x),
точки
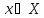 назыв допустимыми, аX
– допустимым, f(x)
– целевая ф-я.
назыв допустимыми, аX
– допустимым, f(x)
– целевая ф-я.
Задача мат-го
программирования (ЗМП) заключ в нахождении
min
ф-ии f(x),
если
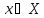 .(1)
.(1)
Под реш ЗМП понимают:
найти точку min ф-ии f(x) на мн-ве X, т.е. найти
 :
: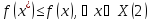 или
или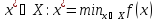 (3) или
(3) или
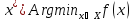 (4)
(4)найти точную нижнюю грань ф-и
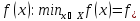 (5)
(5)
Пусть
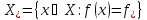
Если
 ,
то найдя
одно из значений (2) – (4), то автоматчески
решается зад (5)
,
то найдя
одно из значений (2) – (4), то автоматчески
решается зад (5)
Если
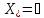 ,
то (5)
приобретает самостоятельное решение
,
то (5)
приобретает самостоятельное решение
Убедиться в том, что ф-я f(x) неограниченна снизу на X, т.е
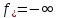
убедиться в том что
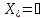
В случаях 3) – 4) говорят что задача (1) не имеет решений
2. Основн. Формы злп. Правила сведения злп к канон.Форме. Геометр.Интерпретация злп. Понятие угловой точки мн-ва.
В ЛП выделяют 2 основных формы задачи:
Каноническая форма ЗЛП
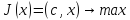
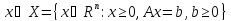
2) Нормальная форма
ЗЛП
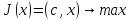

Можно перейти от одной задачи к другой.
Любая ЗЛП сводится к канонической с помощью:
если в исходной постановке ищется min целевой ф-ии
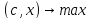 ,
то–(c,x)превращает
исх задачу в задачу о max.
,
то–(c,x)превращает
исх задачу в задачу о max.если
 ,
то соотв ограничения умножаем на (-1),
чтобы превратить правую часть в
положительную.
,
то соотв ограничения умножаем на (-1),
чтобы превратить правую часть в
положительную.если m0, т.е. в исх постановке присутствуют огранич нер-ва то вводятся
 и ограничение нер-ва приводят к виду
и ограничение нер-ва приводят к виду
 и
и
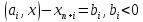
переменные
 назыв свободными, они характеризуют
величину неиспользованного ресурса.
назыв свободными, они характеризуют
величину неиспользованного ресурса.
если на некот переменную не наложено ограничение на знак, то делают замену
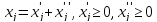 c
соотв изменением целевой ф-и, если
c
соотв изменением целевой ф-и, если
 то
замена
то
замена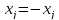
в некот задачах м присутствовать двусторонние прямые ограничения
 ,
тогда правое нер-во относится к основным
ограничениям и применяют 3)
,
тогда правое нер-во относится к основным
ограничениям и применяют 3)двусторонние прямые огранич вида
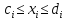 сводятся
к
сводятся
к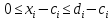 или
или соотв изменениями в целевой ф-и
соотв изменениями в целевой ф-и
Рассм задачу ЛП
внорм форме:
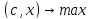
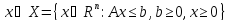
Если множество планов выпуклое, тогда решение сущ., то найдется хотя бы 1 угл.т. мн-ва в которой это решение достигается.
УГЛОВОЙ ТОЧКОЙ
мн-ва
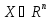 наз.
точка xX,
кот не может быть представлена как точка
отрезка
наз.
точка xX,
кот не может быть представлена как точка
отрезка
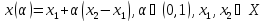
для любых произв
т.
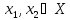
3.Критерий угловой точки множества. Пример.
Рассмотрим задачу
в канонической форме:
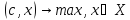 (1),
(1),
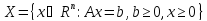 (2).
(2).
Теор(Критерий
угловой точки):Обозначим
ч/з
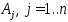 столбцы матр.А,
тогда основные ограничения в системе
(2) можно записать в виде:
столбцы матр.А,
тогда основные ограничения в системе
(2) можно записать в виде:
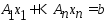 .
Предположим, что матр.А в системе (2)
имеет
.
Предположим, что матр.А в системе (2)
имеет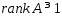 ,
т.е. матр.А ненулевая.Для того, чтобы
точка
,
т.е. матр.А ненулевая.Для того, чтобы
точка была угловой точкой –G
необходимо и достаточно, чтобы сущ.
была угловой точкой –G
необходимо и достаточно, чтобы сущ.
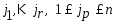 ,
что справедливо рав-во:(3)
,
что справедливо рав-во:(3)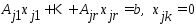 ,
если
,
если
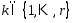 и
и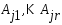 – ЛНЗ.
– ЛНЗ.
Док-во:
Необходимость:Пусть
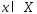 – угловая точка этого мн-ва.а)
– угловая точка этого мн-ва.а)
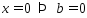 .
Т.к. матр. А в соотношении (2) невырождена,
то сущ.r
ЛНЗ векторов
.
Т.к. матр. А в соотношении (2) невырождена,
то сущ.r
ЛНЗ векторов
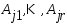 ,
то выполнено
,
то выполнено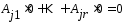 .
т.е. (3) справедливо;
.
т.е. (3) справедливо;
б)
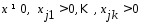 тогда основные ограничения в (2) превратятся
в равенство:
тогда основные ограничения в (2) превратятся
в равенство: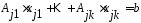 (4).
Рассм.
Рав-во
(4).
Рассм.
Рав-во
 (5).
Построим точки
(5).
Построим точки
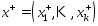 и
и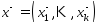 след.
обр.:
след.
обр.:
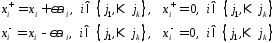
т.к.
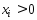 ,то
,то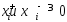 к рав-ву (4) прибавим
и отнимем рав-во (5) умноженное на
к рав-ву (4) прибавим
и отнимем рав-во (5) умноженное на
 получим
что выполняются рав-ва:
получим
что выполняются рав-ва:
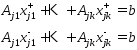 ,
т.е
,
т.е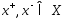 .
Легко видеть
.
Легко видеть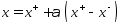 ,
но х – угловая точка след-но
,
но х – угловая точка след-но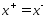 след-но
след-но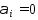 в (5),т.е.вектора
в (5),т.е.вектора – ЛНЗ след-но
– ЛНЗ след-но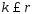
Если
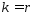 ,
то (3) – доказано, если
,
то (3) – доказано, если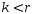 ,
то к векторам
,
то к векторам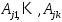 можно добавить вектора
можно добавить вектора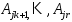 так, чтобы
так, чтобы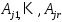 – ЛНЗ, тогда (3) примет вид:
– ЛНЗ, тогда (3) примет вид: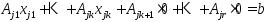 .
.
Достаточность:
пусть для точки
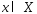 справедливо (3):
справедливо (3):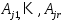 – ЛНЗ, где
– ЛНЗ, где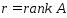 .
Предположим, что
.
Предположим, что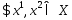 ,
что
,
что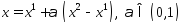 (6).
Покажем, что (6) возможно только при
(6).
Покажем, что (6) возможно только при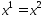 .
Рассмотрим нулевую координату точки
х:
.
Рассмотрим нулевую координату точки
х: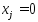 ,
т.е.
,
т.е.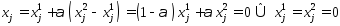 .
Докажем (6) для тех координат, которые
больше 0. Положительными коор-ами т. х
могут быть только те, у которых индекс
.
Докажем (6) для тех координат, которые
больше 0. Положительными коор-ами т. х
могут быть только те, у которых индекс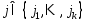 .
Пусть
.
Пусть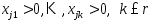 Сл. когда
Сл. когда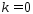 или
или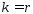 не исключается, тогда система осн-х
огр-ий из (2) преобразуется к виду:
не исключается, тогда система осн-х
огр-ий из (2) преобразуется к виду: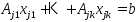 .
Докажем, что
.
Докажем, что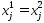 ,
если
,
если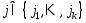 .
Точки
.
Точки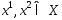 было доказано, что
было доказано, что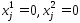 ,
когда
,
когда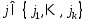 след-но
след-но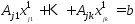 и
и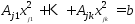 .
Вектора
.
Вектора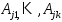 – ЛНЗ, а разложение произвольного
вектора пр-ва по ЛНЗ-векторам явл.
единственным, след-но
– ЛНЗ, а разложение произвольного
вектора пр-ва по ЛНЗ-векторам явл.
единственным, след-но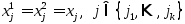 для строго пол-ых координат.
для строго пол-ых координат.
