
- •1.Понятие решения задачи мат. Программиров.
- •2. Основн. Формы злп. Правила сведения злп к канон.Форме. Геометр.Интерпретация злп. Понятие угловой точки мн-ва.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными задачи лп
- •6. Формула приращения целевой функции злп.
- •7. Достаточное условие оптимальности в злп. Достаточное условие неразрешимости злп
- •8. Итерация симплекс–метода
- •11. Нахождение базиса угловой точки. Пример
- •12. Постановка тз. Построение нач. Плана перевозок методом северо-западного угла, методом мин. Элемента.
- •13. Определение закрытой модели тз. Критерий существования решения тз.
- •14. Исследование мн-ва клеток транспортной таблицы
- •15. Достаточное условие минимальности стоимости перевозок
- •16. Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •17. Метод исключения решения задачи на условный минимум. Пример.
- •18. Обобщенное правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств.
- •19. Классическое правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств. Необходимые условия второго порядка в задаче оптимизации типа равенств.
- •20. Достаточные условия экстремума в задаче оптимизации с ограничениями типа равенств
- •21.Опр-ия выпуклого мн-ва, выпуклой функции. Св-ва выпуклых множеств. Сумма выпуклых функций. Св-во неотрицательности остатка выпуклой функции
- •22.Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции
- •26.Теорема о седловой точке функции Лагранжа (достаточные условия оптимальности).
- •27. Критерий существования седловой точки функции Лагранжа для задачи выпуклого программирования.
- •28.Определение двойственной задачи к задаче математического программирования.
- •29. Связь между двойственной и прямой задачами математического программирования.
- •30.Пример решения задачи оптимизации с помощью теории двойственности
- •31.Основные определения в задаче одномерной минимизации. Примеры.
- •33. Метод золотого сечения решения задачи одномерной минимизации.
- •34. Обоснование метода ломаных решения задачи одномерной минимизации.
- •35. Алгоритм и условия сходимости метода ломаных решения задачи одномерной минимизации. Пример. Описание метода ломаных
- •36.Алгоритм метода скорейшего спуска решения змм.
- •37.Алгоритмы метода условного градиента и метода проекции градиента решения задачи многомерной условной минимизации.
- •38.Алгоритм метода покоординатного спуска решения задачи многомерной минимизации. Геометрическая иллюстрация.
- •39.Сходимость метода скорейшего спуска.
- •41. Метод вариаций Лагранжа
- •42. Уравнение Эйлера
- •43. Случаи интегрируемости ур-ния Эйлера. Примеры.
- •44.Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •45.Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования
- •46. Задача вариационного исчисления с движущимся по кривой концом.
- •47. Примеры задач динамического программирования, их особенности
- •48.Принципы динамического программирования и функциональные уравнения Беллмана.
29. Связь между двойственной и прямой задачами математического программирования.
Имеется задача(1):
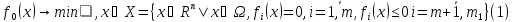
Которую
можно
переформулировать
в(2):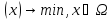 (2)
(2)
Рассм. задачу двойственную к (2). Пусть
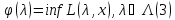
Двойственная
задача имеет вид: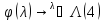
Теор:
Для
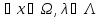 им. место нер-во
им. место нер-во
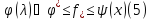
Док-во:
По опр-ию ф-ии
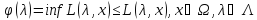 .
Если
.
Если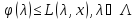
То
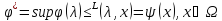 Переходя в последнем нер-ве к точной
нижней грани по мн-ву
Переходя в последнем нер-ве к точной
нижней грани по мн-ву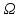 ,
получаем нер-во
,
получаем нер-во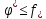 .
Остальные два нер-ва в (5) очевидны.
Теорема доказана.
.
Остальные два нер-ва в (5) очевидны.
Теорема доказана.
Теорема. Если
задачи (2) и (4) имеют решение, т.е. мн-во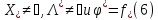 то ф-я Лагранжа
то ф-я Лагранжа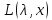 имеет седловую точку на мн-ве
имеет седловую точку на мн-ве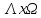 и обратно, если
и обратно, если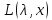 имеет седловую точку, то задачи (2) и (4)
имеют решение.
имеет седловую точку, то задачи (2) и (4)
имеют решение.
Док-во.Необходимость.Пусть
задачи (2) и (4) имеют решение, т.е. выполнено
(5). Возьмем т.
 .
Покажем, что т.
.
Покажем, что т.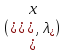 седловая точка ф-ии Лагранжа.
седловая точка ф-ии Лагранжа.
Рассм. значение
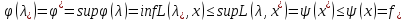
Выполняется усл.
седловой точки, т.к.
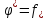 т.е.
т.е.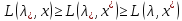
Достаточность.Пусть
ф-я Лагранжа имеет седловую точку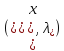 ,
т.е.
,
т.е.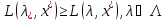
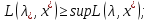
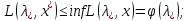
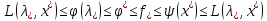
Т.о.
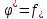 ,
т.е. задача имеет решение.
,
т.е. задача имеет решение.
Следствие1.След. утв. равносильны:
1.Т.
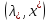 -седловая
точка
-седловая
точка на
на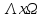 .
.
2. Задачи (2) и (4)
имеют решение, т.е.
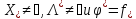
3.Сущ. такие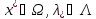 что
что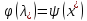
4. Справедливо
равенство
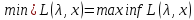
Следствие2. Если
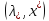 и
и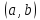 -
седловые точки ф-ии
-
седловые точки ф-ии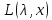 на
на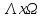 ,
то точки
,
то точки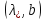 и
и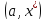 -седловые
точки ф-ии Лагранжа, причем значения
ф-ии
-седловые
точки ф-ии Лагранжа, причем значения
ф-ии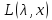 во всех этих точках равны между собой.
во всех этих точках равны между собой.
30.Пример решения задачи оптимизации с помощью теории двойственности
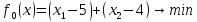
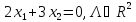


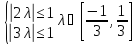
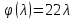
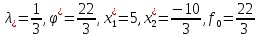
Для правильности
нужно под каждым inf
поставить
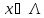 и в место 2 систем поставить оду с 4
уравнениями.
и в место 2 систем поставить оду с 4
уравнениями.
31.Основные определения в задаче одномерной минимизации. Примеры.
Рассмотрим задачу: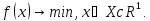
Считаем, что
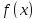 принимает наX
конечные
значения. Произвольное решение этой
задачи будем обозначать ч/з
принимает наX
конечные
значения. Произвольное решение этой
задачи будем обозначать ч/з
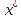 ,
мн-во решений ч/з
,
мн-во решений ч/з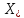 .Таким
обр,
.Таким
обр,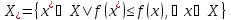 .
.
Опр.
Посл-ть
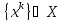 наз. минимизирующей для ф-ции
наз. минимизирующей для ф-ции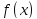 на мн-веX,
если
на мн-веX,
если
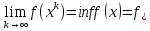
Из опр-ния и существования точной нижней грани следует, что минимизирующая последовательность всегда сущ
Опр.
Посл-ть
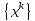 сходится к мн-вуX,
если
сходится к мн-вуX,
если
 ,
где ч/з
,
где ч/з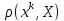 обозначено расстояние от точки
обозначено расстояние от точки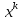 до мн-ва
до мн-ва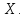
Замеч.
Если мн-во
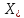 не явл. пустым, то всегда сущ. минимизирующая
посл-ность, сходящаяся к
не явл. пустым, то всегда сущ. минимизирующая
посл-ность, сходящаяся к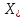 .
.
Пример1:
Пусть
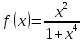 ,
мн-воX
совпадает со всей числовой прямой
,
мн-воX
совпадает со всей числовой прямой
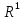 .
Здесь мн-во решений
.
Здесь мн-во решений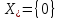 ,
и минимальное значение ф-ции тоже равно
нулю. Посл-ть
,
и минимальное значение ф-ции тоже равно
нулю. Посл-ть явл. минимизир. т.к.
явл. минимизир. т.к.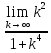 ,
но
,
но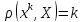 к нулю не стремится при
к нулю не стремится при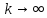 .
.
Опр.
Ф-ция
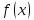 наз. унимодальной на
наз. унимодальной на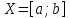 ,
если она непр. на этом отрезке и сущ.
такие числа
,
если она непр. на этом отрезке и сущ.
такие числа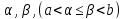 ,
такие что:
,
такие что:
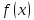 строго монотонно
убывает при
строго монотонно
убывает при
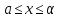 ,
,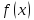 строго монотонно
возрастает
строго монотонно
возрастает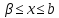 ,
,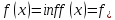 при
при
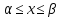 так, что
так, что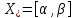 .
.
Если
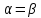 ,
функция наз. строго унимодальной.
,
функция наз. строго унимодальной.
32.Метод деления
отрезка пополам решения задачи одномерной
минимизации. Пусть
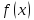 -унимодальна.
Решим задачу
-унимодальна.
Решим задачу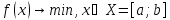 .
.
Выберем 2 точки: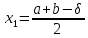 ,
,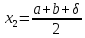 ,
где
,
где ,
являющаяся параметром метода,
,
являющаяся параметром метода,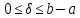 .
Чем меньше значение
.
Чем меньше значение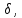 тем больше точность. Заметим что
точки
тем больше точность. Заметим что
точки
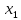 и
и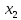 располагаются симметрично относительно
середины отрезка
располагаются симметрично относительно
середины отрезка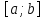 и при малых значениях
и при малых значениях делят его практически пополам.
делят его практически пополам.
Если
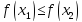 ,
то полагаем
,
то полагаем
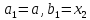
Если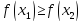 ,
то полагаем
,
то полагаем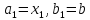
В силу унимодальности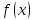 отрезок
отрезок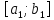 имеет непустое пересечение с множеством
имеет непустое пересечение с множеством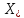 решений задачи и длинна нового отрезка
равна
решений задачи и длинна нового отрезка
равна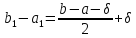 .
.
Пусть найден
отрезок
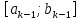 ,
длина кот.
,
длина кот. .
который имеет непустое пересечение с
множеством
.
который имеет непустое пересечение с
множеством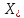 .
.
Вычисляем точки: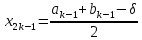 ,
,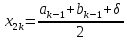
и значение ф-ции
 в
них.
в
них.
Если
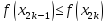 ,
то полагаем
,
то полагаем
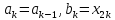
Если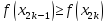 ,
то полагаем
,
то полагаем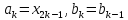
Получим отрезок
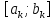 ,
который имеет непустое пересечение с
мн-вом
,
который имеет непустое пересечение с
мн-вом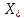 и его длина равна
и его длина равна
Процесс деления
отрезка пополам продолж. до тех пор,
пока не будет достигнута заданная
точность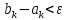 ,
при этом будет проведено
,
при этом будет проведено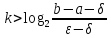 итераций.
итераций.
Так как каждое
деление отрезка пополам требует двух
вычислений значений ф-ции, то для
достижения заданой точности требуется
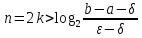 вычислений ф-ции.
вычислений ф-ции.
После определения
отрезка
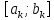 в качестве точки минимума можно взять
в качестве точки минимума можно взять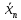 равное:
равное: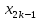 если
если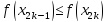 ,
,
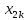 если
если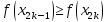
И значение даст приближенное значение
даст приближенное значение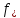 .
При этом погрешность
.
При этом погрешность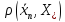 решения, то есть отклонение приближенного
решения от мн-а
решения, то есть отклонение приближенного
решения от мн-а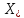 решений не превосходит величины
решений не превосходит величины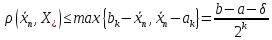 .
.
